PREVISÃO DA OCORRÊNCIA DE TRANSIÇÃO

PREVISÃO DA OCORRÊNCIA DE TRANSIÇÃO
EM ESCOAMENTOS DE CAMADA LIMITE
______________________________________________________
Os critérios a utilizar para proceder à previsão da ocorrência de transição em escoamentos de camada limite
deverão permitir ter em consideração os vários efeitos que condicionam o processo.
________________________________________________________________________
Critério de Michel:
ReT  1.535 Re 0xT.444
Correlação estabelecida com base em resultados experimentais de escoamentos de camada
limite com e sem gradiente de pressão. A transição ocorre para valores dos números de
Reynolds Re  ReT e Re x  Re xT .
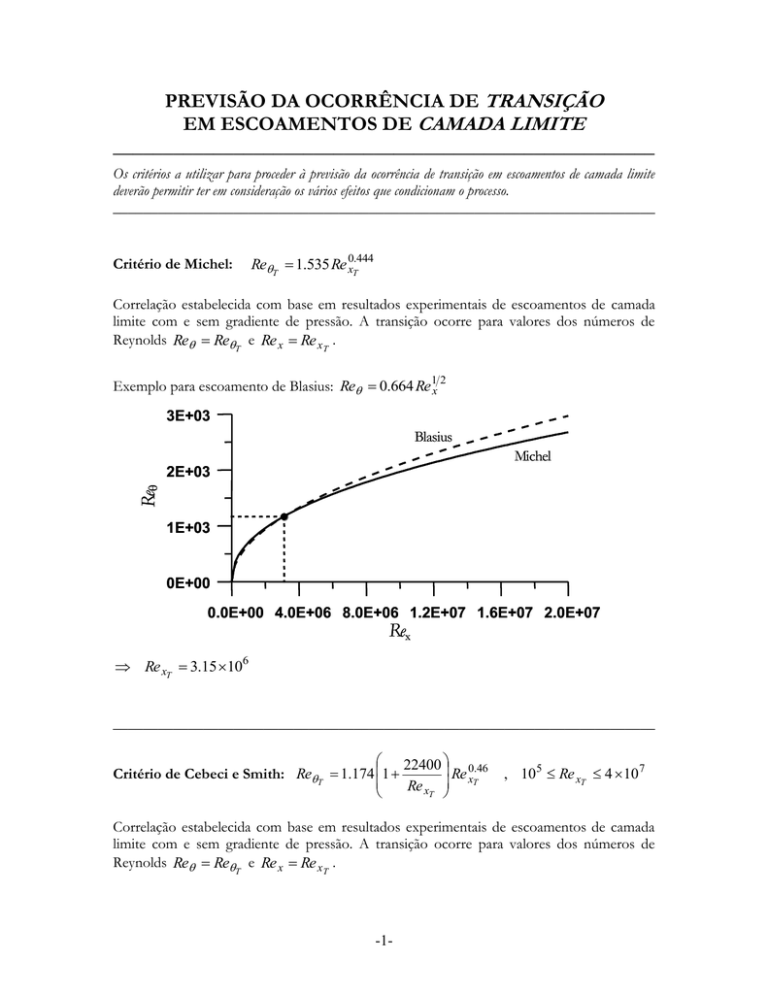
Exemplo para escoamento de Blasius: Re  0.664 Re1x 2
3E+03
Blasius
Michel
Re
2E+03
1E+03
0E+00
0.0E+00 4.0E+06 8.0E+06 1.2E+07 1.6E+07 2.0E+07
Rex
 Re xT  3.15 106
________________________________________________________________________
 22400  0.46
 Re x
Critério de Cebeci e Smith: ReT  1.174 1 
T


Re
xT 

, 105  Re xT  4  10 7
Correlação estabelecida com base em resultados experimentais de escoamentos de camada
limite com e sem gradiente de pressão. A transição ocorre para valores dos números de
Reynolds Re  ReT e Re x  Re xT .
-1-
Critério de Granville:
 2T 
1
xT  xinst

ReT  Reinst  375  exp 6.1  55 2T

,
 2 due
dx ,  0.04   2T  0.024
x inst  dx

xT
Critério estabelecido com base na conjunção de resultados experimentais e informação
referente à estabilidade de escoamentos de camada limite com e sem gradiente de pressão. A
transição ocorre para um valor do número de Reynolds Re  ReT .
O valor de Re inst corresponde ao número de Reynolds a partir do qual a amplificação de
perturbações infinitesimais passa a ser possível na camada limite. Correlações estabelecidas
para a estabilidade de perfis semelhantes de Falkner-Skan, em função do factor de forma
H  , permitem obter este valor:



exp 5.27  17.2 1 H  0.39 1 2
Re

, H  2.5
 inst
H



exp 3.5  2.897 H  22230 H 10
 Re
, H  2.5
 inst 
H


________________________________________________________________________
Critério e N de Smith & Gamberoni / van Ingen:
 A
 
 e NT
A
 0  max
,
NT  9
Critério baseado na análise de estabilidade dos escoamentos de camada limite. A transição
ocorre, em escoamentos bidimensionais, quando a amplitude de perturbações infinitesimais
na camada limite laminar  A atinge um valor cerca de e 9  8000 vezes superior ao valor
inicial  A0  . Toma-se o valor máximo da razão de amplitudes para perturbações também
bidimensionais do tipo onda progressiva, caracterizadas por diferentes comprimentos de
onda. Este é o critério actualmente mais utilizado em projecto.
O valor do factor N é obtido através da integração, ao longo do escoamento, das taxas de
amplificação das perturbações  i  0 consideradas:

N T  max 


 i dx 
x inst


xT
Estas taxas de amplificação são habitualmente obtidas através de uma análise de estabilidade
linear das perturbações, o que obriga à solução de problemas de valor próprio. O método
-2-
seguinte consiste num conjunto de correlações que permitem aplicar este critério de uma
forma apenas aproximada, mas muito mais simplificada:
Método de Habiballah: N T 

ReT
Reinst
S dRe
, sendo o valor de S calculado a partir de:
S  0.0148 H 1.1 , H  3.36


S  0.0329 exp 1.565 H  3.02  , 2.8  H  3.36

S  0.0233 exp 4.126 H  2.8 , H  2.8
________________________________________________________________________
Outros efeitos:

Sucção:
- Considerar alternativamente no critério de Granville o parâmetro:
 2T 

1
xT  xinst
2
x inst 

xT
 due vw 2 C f 

 dx , sendo v w a velocidade de sucção.

Re
2 
 dx ue
Curvatura da superfície:



- Considerar o número de Görtler: GT   Re

R

T
sendo R o raio de curvatura da superfície (côncava).

, 6  GT  9 ,
Intensidade de turbulência:
- Considerar a seguinte modificação ao método de Granville:


ReT  Re inst  206 exp 25.7 2T ln 16.8 Tu   2.77 2T

- Considerar a correlação de Mack no critério e N : NT  8.43  2.4 ln Tu
- Considerar a seguinte correlação para o número de Görtler: GT  9.0 exp  17.3Tu
-3-