Distribuição P(x) - Função massa de probabilidade (v. discretas) f(x

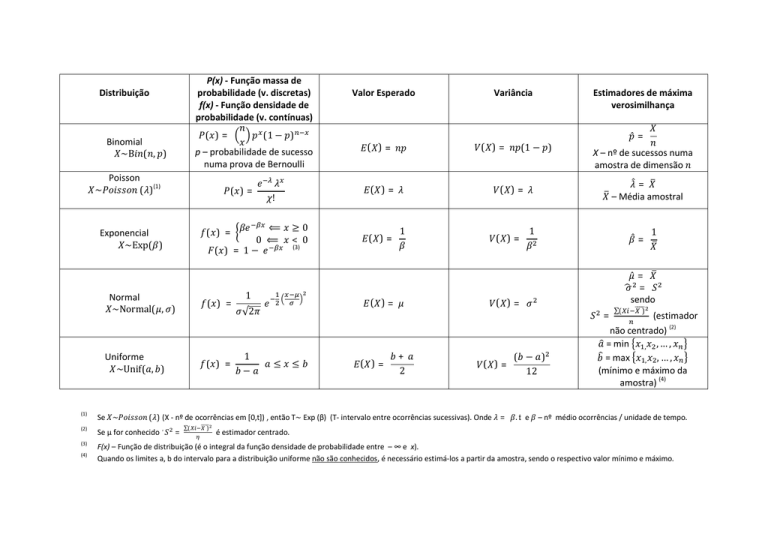
P(x) - Função massa de
probabilidade (v. discretas)
f(x) - Função densidade de
probabilidade (v. contínuas)
Distribuição
( ) =
Binomial
~Β ( , )
~
̂ =
( )=
( )=
( )=
!
⟸ ≥0
0 ⟸ < 0
(3)
( )= 1 −
( )=
Normal
~Normal( , )
( )=
Uniforme
~Unif( , )
Se ~
Estimadores de máxima
verosimilhança
(1 − )
X – nº de sucessos numa
amostra de dimensão
( )=
Exponencial
~Exp( )
(1)
Variância
(1 − )
p – probabilidade de sucesso
numa prova de Bernoulli
Poisson
( )(1)
Valor Esperado
( )=
1
√2
( ) =
1
( ) =
∑(
)
1
=
1
≤
−
( )=
( ) =
≤
( ) =
+
2
( ) =
( ) (X - nº de ocorrências em [0,t]) , então T~ Exp (β) (T- intervalo entre ocorrências sucessivas). Onde
( − )
12
∑(
1
̂ =
=
sendo
)
=
(estimador
não centrado) (2)
= min
, ,…,
= max
, ,…,
(mínimo e máximo da
amostra) (4)
= . e – nº médio ocorrências / unidade de tempo.
(2)
Se µ for conhecido
(3)
F(x) – Função de distribuição (é o integral da função densidade de probabilidade entre – ∞ e x).
Quando os limites a, b do intervalo para a distribuição uniforme não são conhecidos, é necessário estimá-los a partir da amostra, sendo o respectivo valor mínimo e máximo.
(4)
,
=
– Média amostral
( )=
=
é estimador centrado.