LEEC – Teoria dos Circuitos Sinais e fasores

LEEC – Teoria dos Circuitos
Sinais e fasores - 1
Sinais e fasores
1.
Uma onda sinusoidal, f(t), é zero e crescente para t = 2.1 ms, e o máximo positivo seguinte, com o valor de
8.5, ocorre para t = 7.5 ms. Exprimir f(t) na forma:
a. C1 sen(wt + φ), com φ positivo, tão pequeno quanto possível e expresso em graus;
b. C2 cos(wt + β), onde β tem a menor amplitude possível e se exprime em graus ;
c. C3 cos wt + C4 sen wt.
2.
Dadas duas ondas sinusoidais , f(t) = –50 cos wt - 30 sen wt e g(t) = 55 cos wt – 15 sen wt, calcular:
a. a amplitude de cada uma das ondas;
b. determinar o desfasamento entre as duas ondas e mostrar que f(t) está em avanço em relação a g(t).
3.
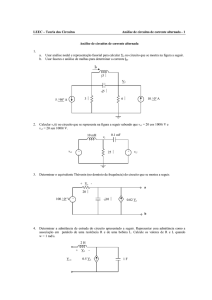
Seja vs = 20 cos 500t no circuito da figura seguinte. Determinar iL(t) depois de simplificar um pouco o
circuito.
5Ω
20 Ω
iL
vs
4.
+
-
60 Ω
20 mH
Calcular a corrente iL(t) no circuito seguinte.
100 Ω
iL
cos 500t V
5.
+
-
0.2 iL
0.3 H
Determinar o valor eficaz de:
a. g(t) = 2 + 3 cos 100t + 4 cos (100t –120º);
b. h(t) = 2 + 3 cos 100t + 4 cos (101t –120º);
c. f(t), que se mostra na figura a seguir.
f(t)
100
- 0.2
0.2
0.4
0.6
-100
t (s)
LEEC – Teoria dos Circuitos
6.
Sinais e fasores - 2
Considere o sinal periódico v(t) com período 4 ms.
a. Determine o seu valor médio Vmed.
b. Determine o seu valor eficaz Vef.
c. Determine a potência média dissipada pela resistência de
10 Ω no circuito seguinte.
(V)
v(t)
12
4
3
v(t)
7.
+
-
(ms)
10 Ω
No circuito da figura a seguir, a representação fasorial da corrente ic é 20ej(40t+30º) A. Determinar a
representação fasorial de vs.
0.08 H
ic
vs
8.
+
-
5Ω
0.01 F
Calcular Zin nos terminais a e b do circuito seguinte se w for igual a: a. 800 rad/s; b. 1600 rad/s.
2 µF
a
300 Ω
600 Ω
b
0.6 H
LEEC – Teoria dos Circuitos
9.
Sinais e fasores - 3
Determinar a admitância de entrada, Yab , do circuito que se mostra na figura a seguir e representá-la como a
combinação paralela de uma resistência R e de uma bobina L, considerando que w = 1 rad/s.
2H
a
+
vL
0.5 vL
b
Soluções
1.
a. f(t) = 8.5 sen(290.9t + 325.0 º)
b. f(t) = 8.5 cos(290.9t - 125.0 º)
c. f(t) = -4.875 cos(290.9t ) + 6.963 sen(290.9t)
2.
a. amplitude de f(t) = 58.31; amplitude de g(t) = 57.01
b. 133.78 º ( f(t) em avanço relativamente a g(t) )
3. iL(t) = 0.67 cos(500t – 26.57 º) A
4. iL(t) = 5.88 cos(500t – 61.93 º) mA
5.
a. Gef = 3.24
b. Hef = 4.062
c. Fef = 33.33
6.
a.19/4 V
7.
Vs = 34.93 ej(40t + 53.63 º) V
8.
a. Zin = 478.0 + j175.65 Ω
b. 13/2 V
c. P = 4.225 W
b. Zin = 587.6 + j119.79 Ω
9.
Yab = 0.5 – j 0.5 S; R = 2 Ω e L = 2H
1F