Análise de circuitos de corrente alternada

LEEC – Teoria dos Circuitos
Análise de circuitos de corrente alternada - 1
Análise de circuitos de corrente alternada
1.
a.
b.
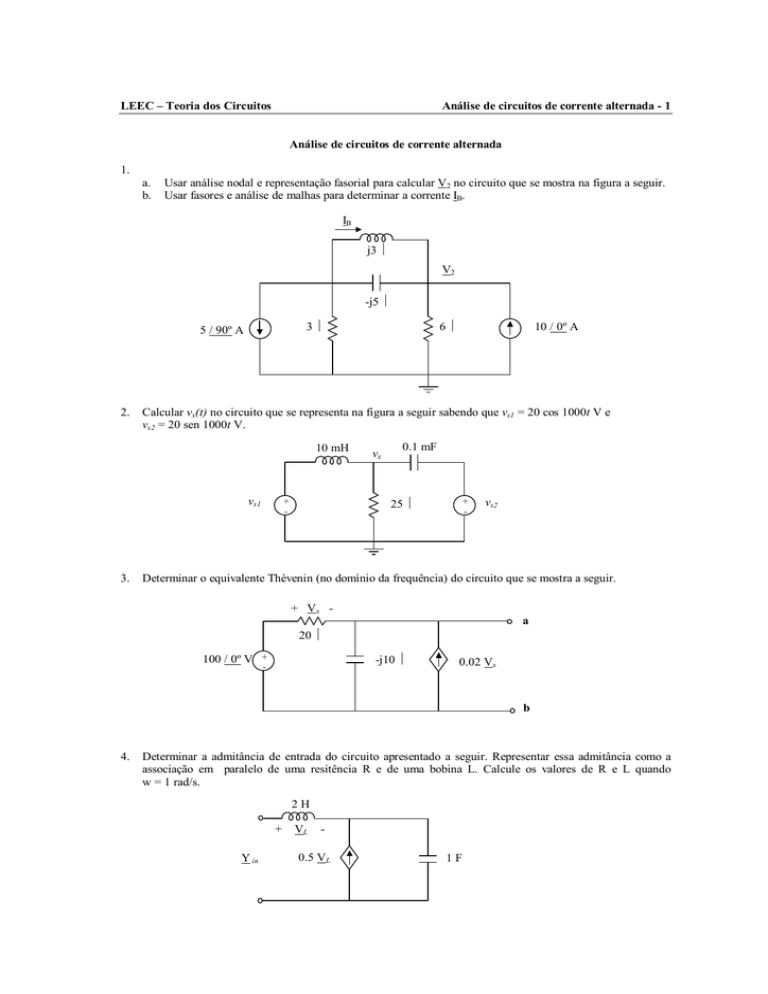
Usar análise nodal e representação fasorial para calcular V2 no circuito que se mostra na figura a seguir.
Usar fasores e análise de malhas para determinar a corrente IB.
IB
j3 Ω
V2
-j5 Ω
3Ω
5 / 90º A
2.
10 / 0º A
Calcular vx(t) no circuito que se representa na figura a seguir sabendo que vs1 = 20 cos 1000t V e
vs2 = 20 sen 1000t V.
10 mH
vs1
3.
6Ω
vx
0.1 mF
25 Ω
+
-
+
-
vs2
Determinar o equivalente Thévenin (no domínio da frequência) do circuito que se mostra a seguir.
+ Vx a
20 Ω
100 / 0º V
-j10 Ω
+
-
0.02 Vx
b
4.
Determinar a admitância de entrada do circuito apresentado a seguir. Representar essa admitância como a
associação em paralelo de uma resitência R e de uma bobina L. Calcule os valores de R e L quando
w = 1 rad/s.
2H
+
Y in
VL
-
0.5 VL
1F
LEEC – Teoria dos Circuitos
5.
Análise de circuitos de corrente alternada - 2
Admitindo que w = 1 rad/s, determinar o equivalente Norton do circuito seguinte. Construir o circuito
equivalente com a associação em paralelo de uma fonte de corrente IN, uma resistência RN e uma bobina LN
ou um condensador CN.
+
1F
VL
a
2H
1 / 0º V
+
-
0.25 VL
b
6.
No circuito a seguir seja is1 = 2 cos 200t A, is2 = 1 cos 100t A e vs3 = 2 sen 200t V. Calcular vL(t).
vs3
1Ω
- +
+
is1
is2
vL
5 mH
-
Soluções
1.
a. V2 = 34.36 / 23.63 º V
b. IB = 13.198 / 154.23 º A
2.
vx(t) = 70.71 cos(1000t – 45 º) V
3.
Vth = 57.35 / -55.01 º V;
4.
Zin=1/Yin = 1 + 1/jω + j2ω Ω; ω= 1 rad/s →Yin = 0.5 – j0.5 S; R = 2 Ω e L = 2H
5.
IN = 0.4 – j0.8 A ; RN = 0.5 + j1 Ω
6.
vL(t) = 2 cos (200t + 90 º) + 0.5 cos (100t +90 º) V
Zth = Vth / 7 = 4.698 – j 6.71 Ω