PROFESSOR AZEVEDO MATRIZES 01

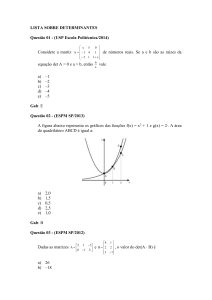
MATRIZES
01 - (UEM PR) Assinale a(s) alternativa(s)
correta(s).
01. O único número real x para o qual
 1 81 
  2 
− 3  
=

⋅ 1



0   log x   243 
3


 0 log 3 x 4

 x
0
3
é
um
número primo.
02. Os valores reais de x para os quais a


matriz A = 
3
2
x −5

x + 1 
7 

8 
satisfaz At = A,
em que At transposta da matriz A, têm
produto igual a - 5.
04. Existe uma única matriz do tipo
 −a

 c

b
,
a 
em que a, b e c são números reais,
cuja inversa seja a própria matriz.
08. A matriz quadrada A = (aij), de ordem 2
× 2, definida por aij = 22 j-i, para todo i = 1, 2
e para todo j = 1, 2, é solução da equação
matricial A2 - kA = 0 para alguma constante
real k.
16.
O
determinante
da
matriz
 senx

 sec x


 − senx
todo
cos x 

tgx senx  é

2
sec x 
π
x real e x ≠ + kπ
2
 x
A = 3
0
0 ,

1
em que x ∈ R .
Assinale as alternativas corretas.
01. A 2 ≠ A para todo x ∈ R .
02. A matriz A é invertível para todo x ∈ R .
04. A inversa da matriz A é distinta da
matriz A para todo x ∈ R .
08. O determinante da matriz A2 é 2.3x.
16. Se B = a b  , com a,b,c,d ∈ R, então
c d 
AB = BA se, e somente se, x = 0.
04 - (UEM PR) Considerando, em um
sistema ortogonal de coordenadas xOy, os
gráficos das funções reais f e g, definidas
no intervalo real [-6, 6], assinale o que for
correto.
1
igual a cos2x, para
(k número inteiro).
02 - (UEM PR) Assinale o que for correto,
considerando as matrizes A = ( a ij ) 3 x 3 e
B = (b ij )
, em que os elementos aij e bij
3x 3
são números reais, para 1 ≤ i ≤ 3 e 1 ≤ j ≤ 3 .
01. Se A é tal que seus elementos aij são
se i ≠ j
definidos por a ij = 10 se
, para 1 ≤ i ≤ 3 e
i= j

1≤ j≤ 3 ,
03 - (UEM PR) Considere a matriz
então A.B=B.
02. ( A − B)( A + B) = A 2 − B 2 .
04. Se B é a matriz inversa da matriz A,
então b ij = 1 , para 1 ≤ i ≤ 3 e
a ij
1≤ j≤ 3 .
08. Se b ij = i + j , para 1 ≤ i ≤ 3 e
então Bt = B.
16. Se b ij = i − j , para 1 ≤ i ≤ 3 e
então det B = 0 .
1≤ j≤ 3 ,
1≤ j≤ 3 ,
01. Os pontos (x, y) do gráfico de f para os
quais -6 ≤ x ≤ -4 satisfazem a equação
y – 5 = x + 4.
02. A função soma f + g é injetora em
[-6, 6].
04. Se c ∈ [2, 6], então, g(c - 4) = 0.
08. Se x ∈ [-2, 6], então, a função produto
de f e g é tal que (f . g) (x) ≥ 0.
16. O número real zero não pertence ao
conjunto imagem da função composta f o g .
05 - (UEM PR) Considere os números
naturais colocados ordenadamente em
linhas da disposição triangular mostrada na
figura e suponha que a distribuição
PROFESSOR AZEVEDO
continue, indefinidamente, obedecendo ao
mesmo padrão.
1
2
5
...
3
4
6
7
8
9
10
11 ...
...
...
...
...
...
...
...
...
...
...
...
...
Sobre o exposto, é correto afirmar que
01. a coluna central não contém números
compostos.
02. a linha de ordem k contém (2k −1)
números naturais, k =1,2, …
04. a quantidade de números naturais
escritos até o final da linha k é k2, k =1,2,…
08. a soma de todos os números naturais
escritos até o final da 20.ª linha é 80.200.
16. o número natural 628 é o quarto número
da 26.ª linha.
06 - (UEM PR) Assinale o que for correto
com respeito às matrizes
8
 0 0 a + 1
x
A = a b
0 , X =  y  e B =  3  ,


 
 
b 
0 a
z 
 - 5
sendo a,
b, x, y e z números reais.
01. A não é uma matriz nula.
02. Se a ≠ 0 , então A possui inversa.
04. Se a = 0 e b ≠ 0 , então a equação
matricial A.X = B possui uma única solução.
08. Se a = −1 , então a equação matricial
A.X = B não possui solução.
16. Se A 2 = A , então a = 0 e b = 1.
07 - (UEM PR) Assinale o que for correto
com respeito às matrizes
1 x

A = 2 x
3 x

− 2
 y

 
1  , B =  2
 2
0 
 
e
 − 1
 
C= 2 
 z 
 
e à equação A ⋅ B = C .
01. Não existem valores reais para x, y e z
que satisfazem a equação dada.
02. Existem infinitos valores reais para x, y
e z que satisfazem a equação dada.
04. Existe apenas um valor real para x, um
para y e um para z que satisfazem a
equação dada.
08. A matriz A é invertível para todo x ≠ 0 .
16. Para obtermos uma solução da equação
dada, devemos ter y = 2 .
08 - (UEM PR) Em um sistema de
coordenadas cartesianas ortogonais no
plano, um ponto P’(x’, y’) é obtido pela
rotação de um ponto P(x,y ) em torno da
origem de um ângulo medindo α graus.
Essa rotação, se ocorrer no sentido antihorário, é definida pelo produto da matriz
 cos α
R = 
 senα
- senα 

cosα 
x
com a matriz P =   ,
y
 x' 
gerando uma matriz P' =   , ou seja, P’ =
y'
 
RP. Rotacionando-se o ponto (2, −4) de um
ângulo de 30º em torno da origem, no
sentido anti-horário, o ponto obtido será
a) 3 + 2, 1 - 2 3
b) 1 - 2 3 , 3 − 2
c) ( 3 - 2, 1 + 2 3 )
d) 1 + 2 3 , 3 − 2
e) 1− 2 3 , 2 - 3
(
(
)
)
(
(
)
)
09 - (UEM PR) Considere a equação
matricial
− a

3
 2
2
a
− 4a
a   x   3
   
− a   y  = 1  .
− 2  z  6
a) Para qual(is) valor(es) de a a equação
matricial possui uma única solução?
Justifique.
b) Determine a solução da equação
matricial para a = −1 , justificando sua
resposta.
10 - (UEM PR) Sobre matrizes, assinale o
que for correto.
a 1
01. Considerando as matrizes A = 
 e
a a 
0
B= ,
0
os únicos valores de a, para os
x 
quais existem infinitas matrizes X =   tais
y
 
que AX=B, são a = 0 e a = 1.
02. Se um sistema de equações lineares de n
equações a n incógnitas é impossível, então
a matriz dos coeficientes associada a ele
não é invertível.
3 2 5 
3 0 −1
04. Considere A = 
 e B=

2 4 2
2 4 2 
. As matrizes X e Y, tais que
PROFESSOR AZEVEDO
2X + Y = 4A + B
,

X − 2Y = −3A + 3B
são
6 2 4
X=

4 8 4
e
a 1

a a 
matriz 
3 4 11
Y=
.
2 4 2 
08. O determinante da matriz quadrada A
de ordem 2, cujo elemento genérico é
a ij = 2i − 3 j + 5 , é igual a –12.
16. Sabendo-se que as matrizes M e N,
ambas de ordem 4, são inversas entre si, o
determinante da matriz P = 7MN é 2401.
11 - (UEM PR) Sobre matrizes e
determinantes, assinale a(s) alternativa(s)
correta(s).
01. Se o determinante de uma matriz
quadrada A é 10 e se a segunda linha for
multiplicada por 4 e a quinta linha por
02. Os possíveis valores de a para que a
admita inversa são a = 0 ou
a =1.
04. Se A e B são matrizes quadradas de
mesma ordem tais que det( A ) = a e
det( B − A ) = b com a e b números reais, então
det( B) = b + a .
08. Se A e B são matrizes quadradas de
mesma ordem, m e n são números naturais
tais que det( AB) = 2 m e det( A ) = 2 n , então
m
det( B) = 2 n
.
 4 0  0 0   4 0  0 0 

 ≠ 

 .
 2 0  3 6   2 0  − 3 1 
16. 
1
,
2
então o determinante da matriz resultante é
20.
02. Uma matriz quadrada A de ordem 3 é
tal que seus elementos satisfazem aij + aji =
0 para todo 1 ≤ i, j ≤ 3. Então, det(A) ≠ 0.
04. Se uma matriz quadrada A de ordem n
tem determinante satisfazendo a equação
det(A2) + 2det(A) + 1 = 4, então o det(A) é
igual a 1 ou – 3.
08. Se A é a matriz dada por
 k 1 − 1


1 1 2  ,
 k 0 k 
então o único valor de k que torna o
determinante de A2 nulo é zero.
16.
Se A = B ⋅ C, onde
3 2 4 


C = 0 13 23  ,
0 0 − 4
1

B =  13
4
 3
0 0

1 0

1 1

e
então o determinante de A é
igual a – 4.
12 - (UEM
determinantes,
corretas.
01. Se A é uma
número natural
det(A −1 ) =
1
3n
.
PR) Sobre matrizes e
assinale as alternativas
matriz quadrada e n é um
tal que det( A ) = 3n , então
GABARITO:
1) Gab: 24
2) Gab: 25
3) Gab: 29
4) Gab: 29
5) Gab: 14
6) Gab: 25
7) Gab: 12
8) Gab: A
9) Gab:
10) Gab: 23
11) Gab: 21
12) Gab: A
PROFESSOR AZEVEDO