colégio nossa senhora da piedade

COLÉGIO NOSSA SENHORA DA PIEDADE
Programa de Recuperação Paralela
2ª Etapa – 2012
Disciplina: Matemática
Ano: 2012
Professor (a): Ana Cristina
Turma: 2o FG/TI
 Caro aluno, você está recebendo o conteúdo de recuperação.
 Faça a lista de exercícios com atenção, ela norteará os seus estudos.
 Utilize o livro didático adotado pela escola como fonte de estudo.
 Se necessário, procure outras fontes como apoio (livros didáticos, exercícios além dos
propostos, etc.).
 Considere a recuperação como uma nova oportunidade de aprendizado.
 Leve o seu trabalho a sério e com disciplina. Dessa forma, com certeza obterá sucesso.
 Qualquer dúvida procure o professor responsável pela disciplina.
Conteúdo
- Sistemas Lineares
- Geometria de Posição e Poliedros
- Áreas de Superfícies Planas
- Prismas
Recursos para Estudo / Atividades
- Fascículos usados:
 Sistemas Lineares
 Geometria de posição e poliedros
 Sólidos Geométricos
- Caderno
- Diversificadas
- Módulos
Rede de Educação Missionárias Servas do Espírito Santo
Colégio Nossa Senhora da Piedade
Av. Amaro Cavalcanti, 2591 – Encantado – Rio de Janeiro / RJ
CEP: 20735042 Tel: 2594-5043 – Fax: 2269-3409
E-mail: [email protected]
Home Page: www.cnsp.com.br
ENSINO MÉDIO
Área de Conhecimento: Matemática e suas Tecnologias
Disciplina: Matemática
Data : 14/09/2012
Professora: Ana Cristina
Etapa: 2ª
Nome do (a) aluno (a):
2º Ano
Turma:
Nº
2 FG/2AD
BLOCO DE ATIVIDADES / EXERCÍCIOS PROPOSTOS
1) Um poliedro convexo é constituído por 20 ângulos triédricos. Quantas arestas tem esse poliedro?
2) Um poliedro convexo é constituído por 20 arestas e seu número de vértices é igual ao número de faces.
Quantas faces formam esse poliedro?
3) O número de arestas de um octaedro convexo é o dobro do número de vértices. Quantas arestas possui
esse poliedro?
4) Existe poliedro convexo que possua 20 vértices, 12 faces e 18 arestas? Por quê?
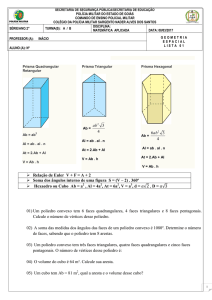
5) A figura representa a planificação da superfície de um prisma triangular. CALCULE o volume desse
prisma.
6) Uma indústria embala seus produtos em caixas de papelão com forma de prisma reto, cujas medidas
estão indicadas na figura. Sabendo que em certa semana foram utilizadas 20 000 dessas caixas, quantos
metros quadrados de papelão, desconsiderando desperdícios, foram utilizados para confeccionar todas as
caixas?
7) (ENEM) Eclusa é um canal que, construído em águas de um rio com grande desnível, possibilita a
navegabilidade, subida ou descida de embarcações. No esquema a seguir, está representada a descida de
uma embarcação, pela eclusa do porto Primavera, do nível mais alto do Rio Paraná até o nível da jusante.
A câmara dessa eclusa tem comprimento aproximado de 200 m e largura a 17 m. A vazão aproximada da
água durante o esvaziamento da câmara é de 4 200 m3 por minuto. Assim, para descer do nível mais alto
até o da jusante, uma embarcação leva cerca de:
(A) 2 minutos
(B) 5 minutos
(C) 11 minutos
(D) 16 minutos
8) A área da superfície de um cubo é 384 cm2. Em quantos centímetros deve ser aumentada cada aresta
desse cubo para que seu volume passe a ser 1728 cm3 ?
9) As dimensões - comprimento, largura e altura - de um paralelepípedo reto-retângulo são 20 cm, 12 cm e
9 cm. CALCULE a medida de uma diagonal desse paralelepípedo.
10) DETERMINE o volume de um prisma reto de 20 cm de altura cuja base é um triângulo retângulo de
catetos 8 cm e 15 cm.
11) ACHE o número de faces de um poliedro convexo que possui dezesseis ângulos triédricos.
12) (UNESP-SP) CONSIDERE o sólido resultante de um paralelepípedo retângulo de arestas medindo x,
x e 2x, do qual um prisma de base quadrada de lado 1 e altura x foi retirado. O sólido está representado pela
parte escura da figura.
DETERMINE o volume desse sólido, em função de x.
13) Um prisma reto tem base quadrada de diagonal 2 cm. CALCULE o volume do prisma sabendo que
sua diagonal mede 4 3 cm.
14) CLASSIFIQUE o sistema:
 3x  5 y  0

 2x  y  0
kx  5 y  0
15) DETEMINE o valor de K em 
a fim de que esse sistema seja possível e determinado.
5 x  ky  0
16) RESOLVA o sistema de duas equações aplicando a regra de Cramer:
 x  2 y  12

 x y 3
17) ESCREVA o sistema de equações correspondente a:
2 5   x   12 
 1

   

4 0  .  y  =   11
 2
 3 3 1 z   9 

   

18) No cubo da figura a seguir, as arestas medem 4cm. Quanto mede a diagonal AB?
19) Quantos cubos A precisa-se empilhar para formar o paralelepípedo B?
20) Sabendo que uma diagonal de uma face de um cubo mede 5 2 cm, CALCULE a medida da diagonal
desse cubo.