Distribuições de Probabilidades

Universidade Federal de Minas Gerais
Departamento de Estatística – ICEx
Métodos Computacionais para Estatística
Distribuições de Probabilidades
1.
Variáveis Discretas - Função de Probabilidades e Função Distribuição
Acumulada.
No Minitab, através do caminho Calc + Probability Distributions é possível
calcular probabilidade relativas a vários modelos probabilísticos. Neste grupo
de funções do Minitab pode-se calcular:
• Probability (PDF)
• Cumulative probability (CDF)
• Inverse cumulative probability (InvCDF)
É possível a obtenção dos mesmos resultados teclando os comandos adequados
diretamente no console, desde que o mesmo esteja habilitado.
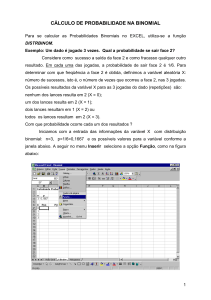
Exemplos de probabilidades binomiais de X~Binomial (10; 0,6).
MTB > pdf;
SUBC> binomial 10 0,6.
MTB > cdf;
SUBC> binomial 10 0,6.
Probability Density Function
Binomial with n = 10 and
p = 0,600000
Cumulative Distribution Function
Binomial with n = 10 and
p = 0,600000
x
0
1
2
3
4
5
6
7
8
9
10
2.
3.
P( X = x )
0,0001
0,0016
0,0106
0,0425
0,1115
0,2007
0,2508
0,2150
0,1209
0,0403
0,0060
x
0
1
2
3
4
5
6
7
8
9
10
P( X <= x )
0,0001
0,0017
0,0123
0,0548
0,1662
0,3669
0,6177
0,8327
0,9536
0,9940
1,0000
Variáveis Contínuas - Função de Densidade de Probabilidades e Função
Distribuição Acumulada.
Através do mesmo caminho é possível calcular probabilidades referentes a
vários modelos de distribuições contínuas.
Procedimentos para Cálculo de Probabilidades e Montagem de Gráficos:
Exemplo para a distribuição binomial
a) Valores de Sucesso (k):
1. Na barra de ferramentas, escolha Calc;
2. Selecione Make Patterned Data.
3. Selecione Simple Set of Numbers
Assinale na tela:
1. Store patterned data in: C1
2. From first value: 0
3. To last value: 20
4. In steps of: 1
5. List each value: 1
6. List the whole sequence: 1
b) Cálculo de Probabilidades – Binomiais:
1. Na barra de ferramentas, escolha Calc;
2. Selecione Probability distributions;
3. Selecione Binomial
Observações:
Na primeira parte da tela, assinale o que deseja calcular:
• Probability: probabilidade no ponto, ou seja, p(x) = P(X = x);
• Cumulative probability: probabilidade acumulada, F(x) = P(X ≤ x);
• Inverse cumulative probability: inverso da probabilidade acumulada, ou
seja, x tal que P(X ≤ x) = pac.
Na segunda parte da tela, informe os parâmetros do modelo Binomial:
• Number of trials: número de realizações do experimento: n;
• Probability of success: probabilidade de sucesso: p.
A terceira parte corresponde à entrada de dados, ou seja, se você assinalou
Probability ou Cumulative probability, você deve fornecer o valor de x em
Input constant, ou os valores de x em Input column. Neste último caso, a coluna
contendo os valores de x já deve estar pronta. Se você assinalou Inverse cumulative
probability, você deve informar o valor pac (Input constant ) ou os valores de pac
(Input column). Caso haja interesse, é possível guardar os resultados assinalando
Optional storage e indicando onde devem ser armazenados.
4.
Exercícios
a) Gerar a distribuição de probabilidades e a função de distribuição
acumulada para uma v. a. X ~Binomial(15, 0,48) e X~Poisson (4).
b) Se X tem distribuição Binomial com parâmetros n = 10 e
p = 0,5
p = 0,25
p = 0,9
i. Faça os gráficos das distribuições de X e da função de
distribuição acumulada. Qual a diferença entre os gráficos?
O que ocasionou a diferença?
ii. Calcule a média nos três casos e localize cada uma no
respectivo gráfico.
c) A experiência indica que 40% das pessoas que entram em uma loja de
computadores fazem compras. Se 9 pessoas entram na loja, determine
a probabilidade de:
i. sete ou menos pessoas façam compras. 99,62%;
ii. apenas uma pessoa faça compras;
iii. mais que 4 pessoas façam compras;
iv. de 3 a 5 pessoas façam compras.
d) Considerando 600 famílias com 3 crianças e admitindo que as
probabilidades de nascimentos de meninos e meninas em uma família
sejam iguais, calcule o número esperado de famílias com:
i. Nenhum menino;
ii. 2 meninos;
iii. Pelo menos 1 menino;
iv. Exatamente 3 meninas.
e) Sabe-se que uma lâmpada comum tem uma probabilidade de 0,90 de
durar mais de seis meses. Se uma pessoa instalou 20 dessas lâmpadas,
determine a probabilidade dela ter que substituir:
i. No máximo 2 lâmpadas antes de seis meses;
ii. Mais que duas lâmpadas antes de seis meses;
iii. De duas e quatro lâmpadas antes de seis meses;
iv. Nenhuma lâmpada antes de seis meses;
v. Para cada lote de 50 lâmpadas, qual o número médio de
lâmpadas que deverão ser substituídas depois de seis meses
de uso?
f) Calcular a função de probabilidade de uma variável aleatória com
distribuição de Poisson com média λ= 5, para valores de
k= 0, 1, 2, ..., 30
g) Calcular a função de probabilidade de uma Variável Aleatória
com distribuição binomial com parâmetros n=500 e p=0,01.
Compare com os valores calculados no exercício anterior.
h) O total de pontos obtidos no vestibular de uma universidade é
uma variável aleatória normal com média 550 e desvio-padrão
120.
i. Determine a probabilidade de um candidato obter:
1. Mais de 700 pontos;
2. Menos de 200 pontos;
3. Entre 200 e 700 pontos.
ii. Determine a pontuação acima da qual encontram-se
os 5% melhores candidatos.
iii. Determine a faixa de pontuação, simétrica em torno
da média, que contenha aproximadamente 85% dos
candidatos
i) Suponha que numa universidade, a altura dos estudantes do
sexo masculino tenha distribuição normal com µ=170 cm e
σ=10 cm. Calcule:
i. P(X>190);
ii. P(150<X<190);
iii. P(X<160);
iv. A percentagem esperada de estudantes com altura
entre 150 e 190 cm.
j) Em um processo industrial, as peças com mais de 22 kg ou
menos de 18 kg são consideradas defeituosas. O processo atual
produz 30% de peças defeituosas. Foi proposta a troca por um
processo em que o peso das peças tem distribuição Normal
com média 21 kg e desvio padrão 0,9 kg. Qual a proporção de
peças defeituosas produzidas pelo novo processo? Deve ser
feita a troca?
A Distribuição Normal como aproximação de distribuições
discretas
k) Com o auxílio da distribuição normal,
obtenha uma
aproximação da probabilidade de que, no máximo 12 de 50
pacientes venham a ter dor de cabeça em conseqüência da
ingestão de um certo remédio, se a probabilidade de um tal
evento
é
igual
a
0,22.
0,6957
Recalcule a probabilidade pedida usando o modelo binomial e
determine o erro percentual da aproximação.
l) Uma companhia aérea sabe que o número de malas que ela
perde semanalmente em certa rota é uma variável aleatória que
tem distribuição aproximadamente Normal com média 26,2 e
desvio padrão 5,8. Determine as probabilidades de que, em uma
semana, a companhia aérea perca nesta rota
i. Exatamente 22 malas;
ii. No máximo 22 malas;
iii. No mínimo 22 malas.