Distribuição de Probabilidade

Distribuição de Probabilidade
 Prof.: Joni Fusinato
 [email protected]
 [email protected]
Distribuição de Probabilidade
 Em Estatística, uma distribuição de probabilidade descreve a
chance que uma variável pode assumir ao longo de um
espaço de valores.
 É uma função cujo domínio são os valores da variável (x1,
x2, ...) e cuja imagem são as probabilidades (p1, p2, ...) da
variável assumir cada valor do domínio.
 O conjunto imagem deste tipo de função está sempre restrito
ao intervalo entre 0 e 1.
 Uma distribuição de probabilidade pode ser discreta ou
contínua.
 É comum o uso de funções que se ajustem à distribuição de
probabilidade.
Distribuições de Probabilidades
para V. A Discretas
Distribuição Uniforme Discreta
Distribuição de Bernoulli
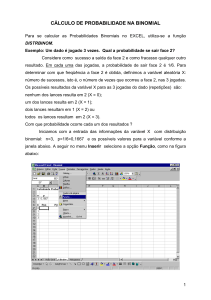
Distribuição Binomial
Distribuição de Poisson
Distribuição Geométrica
Distribuição Uniforme Discreta
Distribuição de Bernoulli
O que as perguntas abaixo têm em comum?
– Diminuirão os casos de dengue no próximo ano?
– Haverá uma alta do trigo este ano?
– Uma moeda lançada vai dar coroa?
O tipo de resposta:
- Sim ou não.
Distribuição de Bernoulli
Distribuição Binomial
Considere agora as seguintes perguntas:
– Quantas vezes vão ocorrer casos de dengue no próximo ano?
– Quantas vezes vai haver uma alta do trigo nos próximos 20
anos?
– Se lançarmos uma moeda 5 vezes, quantas vezes teremos
cara?
Muitas vezes, não queremos saber apenas se algo
ocorre ou não. Queremos saber quantas vezes ela
ocorre.
Distribuição Binomial
A distribuição binomial resolve problemas de contagem
respondendo perguntas do tipo “quantos” em experimentos
onde:
 Há dois resultados possíveis,
 A probabilidade de sucesso é constante e
 os eventos são independentes.
Distribuição Binomial
Distribuição de Poisson
 A diferença entre a distribuição Binomial e a de Poisson é
que a binomial tem um número máximo possível de
ocorrências e a de Poisson não tem.
EXEMPLOS:
 Se lançarmos uma moeda 3 vezes, qual é o número
máximo de coroas que se poderá obter?
 Quantas pessoas estarão na fila no horário de pico?
 Quantos acidentes vão acontecer este ano?
Uma pergunta como “quantas pessoas estarão na fila no
horário de pico” não pode ser respondida por uma distribuição
binomial.
Distribuição de Poisson
Nestes exemplos, interessa contar quantas vezes alguma
coisa acontece em um espaço contínuo de tempo.
Quando isso acontece, podemos usar a distribuição de
Poisson
Distribuição Geométrica
 Repetição de um experimento com distribuição de Bernoulli
(sucesso ou fracasso) até a obtenção do primeiro sucesso.
Distribuições de Probabilidades
para V. A Contínuas
Distribuição Uniforme Contínua
Distribuição Normal
Distribuição Χ2 (Qui Quadrado)
Distribuição t de Student
Distribuição Exponencial
Distribuição Normal
Distribuição Normal
Distribuição Normal
Distribuição Normal - Exemplo
A área sob a curva
entre quaisquer dois
valores de x1 e x2
dependerão de µ e σ