NÚMEROS COMPLEXOS.

NÚMEROS COMPLEXOS
5. OPERAÇÕES COM NÚMEROS COMPLEXOS:
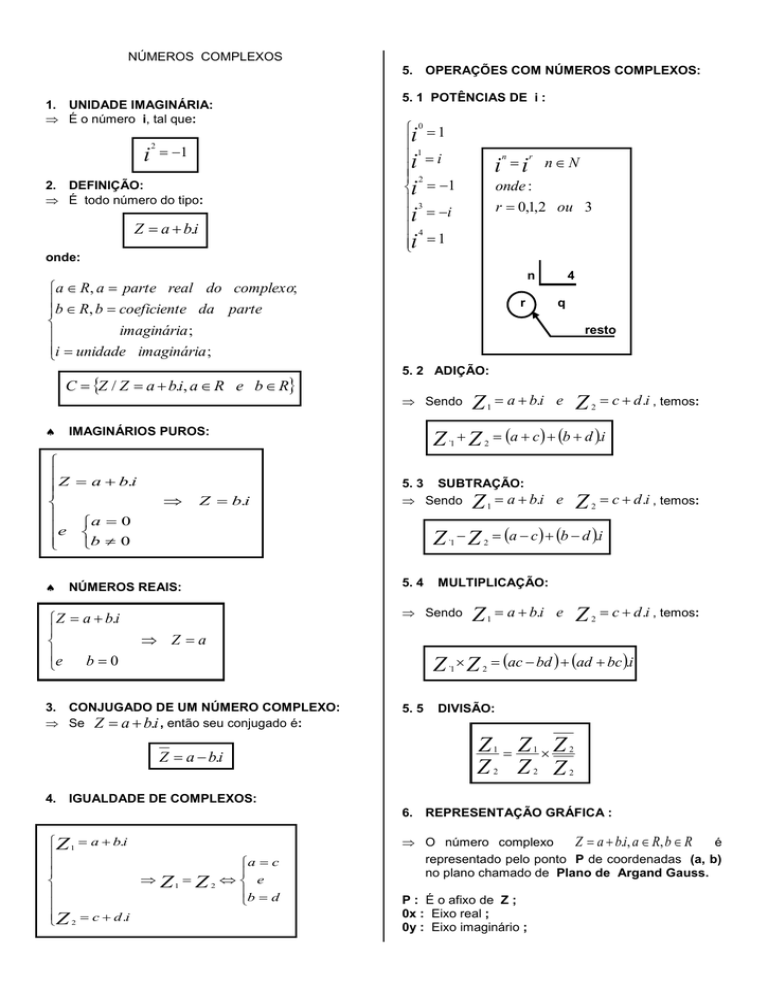
5. 1 POTÊNCIAS DE i :
1. UNIDADE IMAGINÁRIA:
 É o número i, tal que:
i
2
 0 1
i
i1  i
 2
i  1
3
i  i
 4
i  1
 1
2. DEFINIÇÃO:
 É todo número do tipo:
Z  a  b.i
onde:
i i
n
onde :
r  0,1,2 ou 3
n
a  R, a  parte real do complexo;
b  R, b  coeficiente da parte


imaginária ;

i  unidade imaginária ;
C  Z / Z  a  b.i, a  R e b  R

r
 Sendo

Z  b.i
Z  a  b.i


e
b0

 a  b.i e
2
 a  c   b  d .i
Z
5. 3 SUBTRAÇÃO:
 a  b.i e
 Sendo
1
Z
a  0

b  0
Z Z
`1
5. 4
NÚMEROS REAIS:
1
Z
`1

q
5. 2 ADIÇÃO:
Z Z
 a  b.i
4
resto
IMAGINÁRIOS PUROS:


Z



e


n N
r
Z
2
2
 c  d .i , temos:
 c  d .i , temos:
 a  c   b  d .i
2
MULTIPLICAÇÃO:
 Sendo
Z
1
 a  b.i e
Z
2
 c  d .i , temos:
 Z a
Z Z
`1
3. CONJUGADO DE UM NÚMERO COMPLEXO:
 Se Z  a  b.i , então seu conjugado é:
Z  a  b.i
5. 5
2
 ac  bd   ad  bc .i
DIVISÃO:
Z
Z
1
2

Z Z
Z Z
1
2
2
2
4. IGUALDADE DE COMPLEXOS:
6. REPRESENTAÇÃO GRÁFICA :
Z 1  a  b.i







Z 2  c  d .i

Z
1

Z
2
a  c

 e
b  d

Z  a  b.i, a  R, b  R é
 O número complexo
representado pelo ponto P de coordenadas (a, b)
no plano chamado de Plano de Argand Gauss.
P : É o afixo de Z ;
0x : Eixo real ;
0y : Eixo imaginário ;
n  N , n  2 e k  0,1,2,....., n  1
y
b
P
TESTES
Z
1. (FRANCO) Os números complexos x e y para

os quais
0
a
x
 MÓDULO:
 É um número real que representa a distância do
afixo de Z à origem do sistema de coordenadas.
Z  a 2  b2
 ARGUMENTO:
 É o ângulo  determinado pelo eixo real 0x e o
segmento 0P, medido no sentido
anti-horário
a partir do eixo real.
cos  

a
Z
e sen  
Z
 Z 1 .cos  1  i. sen  1 
e
 Z2 .cos  2  i. sen  2  , temos:
2
Z Z
1
2
Z
Z
Z
1

2

 Z 1 .cos  1  i. sen  1 
 Z2 .cos  2  i. sen  2  , temos:
2
Z1
Z2
e y
são:
que
y2
y6
y0
y  1
e
e
e
e


c) 7
d) 8
e) 10
e



a) 3 e 2
c) 1 e 2
b) 1 e 3
d) 1 e i
5. (FRANCO) Se
U V
.cos 1   2   i. sen  1   2 
U  4  3.i e V  5  2.i , então
é:
20  6.i
26 13.i
b)
d)
6. (FRANCO)
Se
a)
c)
e) n. d. a
14  7.i
14  7.i
e)
26  7.i
POTENCIAÇÃO:
Z

Z
1
3.x  3. y.i  3. y  6  3.i
b) 6

Z
x
4. (FRANCO) Os valores de x e y, com x, y  R ,
que
satisfazem
a
equação
2  5.i .x  1  3.i . y  8  9.i  0 são:
 Z1  Z2 .cos1   2   i. sen1   2 
Sendo
Os números reais
3. (FRANCO) Qual é o valor de m para que o
produto 2  m.i . 3  i seja um imaginário puro
?
a) 5
 Divisão na Forma Trigonométrica:

2. (FRANCO)
satisfazem

 Multiplicação na Forma Trigonométrica:
1
1 i
2
e y  1 i
y 1
y
e
e) n. d. a
Z  Z .cos   i. sen  
Z
y i
e) n. d. a
x4
b) x  8
c) x  2
d) x  1
FORMA TRIGONOMÉTRICA:
 Sendo
x 1 e
1 i
b) x 
2
c) x  1  i
d) x  0 e
a)
a)
b
Z
 x  y.i  i
são:

 x.i  y  2i  1
n
 Z .cosn   i. sen n 
n
RADICIAÇÃO:
k
 
2 
2 

 n Z .cos  k.   i. sen   k . 
n 
n 
n
 n
f (Z )  Z 2  Z  1 , então
f (1  i ) é igual a:
a) i
c) i  1
b)
d)
1  i
i 1
7. (FRANCO) O quociente
Onde:
a)
1 2.i
b)
2i
e)  i
8i
é igual:
2i
e)
3  2.i
c)
2  2.i
2  3.i
d)
8. (FRANCO)
1  3i
é:
2i
O conjugado do número complexo
 1  7i
5
1  2i
c)
7
1 i
5
 1  7i
d)
5
b)
1 i
5
e)
9. (FRANCO) O produto 2  b.i pelo seu conjugado
é 13, com b  R . Os positivos valores de b são:
b)  2
a) 0
3
 13
e)
Z  5i
Dados
W
e
 3  2i ,
1
 W é:
então
Z
83 51
 i
26 26
1 39
 i
c)
29 29
a)
b)
8i
d)
5
2
 i
13 13
b) i
c)  1
i14 ?
d) 1
e)
b) 1
c) 50
1  i
1 i
b)
d)
14. (FRANCO) Se Z
assumir os valores:
1,1, i,i
c) 1,i
a)
d) 100
e) i
b)
1  i
1 i
e) 1
 i 2 n , n  N , então Z pode
1,1
d)
1
2
e)
1
4
16 e
7
16
b)
16 e
c)
16 e
4
3
d)
8 e
5
6
8 e
e)
2
3
4
3
satisfaz a condição
Z 1  3 ?
Uma Circunferência
Uma Reta
Uma Elipse
Uma Parábola
n. d. a
(FRANCO)
O módulo do número complexo
1  3i 4
a) 256
é:
b) 100
c) 81
d) 64
20. (FRANCO) O número complexo
forma trigonométrica, é:
e) 16
2  2i , na



2. Cos  i.Sen 
6
6




b) 2. Cos  i.Sen 
4
4

a)



2. Cos  i.Sen 
3
3

3
3 

 i.Sen 
d) 2. Cos
4
4 

5
5 

 i.Sen 
e) 2. Cos
4
4 

c)
e) n. d. a
21. (FRANCO) Seja o número complexo Z, tal que
d) 1
15. (FRANCO) O número complexo
a:
i 3
é:
3 i
3
c)
a)
14.i
13. (FRANCO) O primeiro termo de uma P.G de
razão i, de 4.n  3 termos e de último termo
1  i é:
a)
c)
b) 1
e) n. d. a
Z  8 3  8i são, respectivamente:
a)
b)
c)
d)
e)
19.
S100 é a soma dos cem primeiros
termos da P.A de primeiro termo  99  i e
S100
razão 1  i , então
é igual a:
 99  101.i
100.i
1  i
1  i
17. (FRANCO) O módulo e o argumento do complexo
e) n. d. a
12. (FRANCO) Se
a)
b)
d)
18. (FRANCO) Que lugar geométrico descreve o afixo
Z  x  y.i quando
do número complexo
11. (FRANCO) Qual o valor de
a)  i
a) 0
 13
d)
10. (FRANCO)
1 i
1 i
16. (FRANCO) O módulo de
a)
c)
a)
c)
i
99
i
1 i
Z  Z  2  4i  2Z.i . A imagem de Z no plano
de Argand-Gauss é um ponto pertencente ao:
75
é igual
a) Eixo Real
b) Eixo Imaginário
c) Segundo Quadrante
d) Terceiro Quadrante
e) Quarto Quadrante
e)
22. (FRANCO) Se o módulo de um número complexo
é igual a
5
,a
2 e seu argumento é igual a
4
expressão algébrica deste número é:
a)
c)
1 i
1 i
b) 2.i
d) i
e)
1  i
a)
b)
c)
d)
e)

15. Cos1350  i.Sen1350
8. Cos75  i.Sen75
8. Cos1350  i.Sen1350
15. Cos15  i.Sen15
15. Cos75  i.Sen75










2  2 2.i
26. (FRANCO)
produto

3 1
 i
2 2
1 i
b)
1 i
c)
1 1
 i
2 2
d)
1
1 i
2
As
60

c) 204
e)
cinco
raízes
120

d) 216
2
complexo
2
2

i
2
2
quintas


2 Cos18  i.Cos18 
2 Cos144  i.Sen144 
2 Cos216  i.Sen216 
c)
5
 2,1 e raio 5.
d)
e) n. d. a
três
e) n. d. a
2 Cos18  i.Sen18
2,1 e raio 5.
dos
b)
30. (FRANCO) Uma raiz Quinta de 2 é:
5
5






números

3  3 3.i
d) 6  3.i
e)
os
3  2.i
complexos
Z1  4(Cos60  i.Sen60 ) e
1
Z 2  (Cos90  i.Sen90 ) . A forma algébrica do
2
complexo Z  Z1.Z 2 é:
a)
a)
b)
0,5 e raio 2.
b)
Sejam
número
e)
quartas do número complexo:
5
é igual a:
c)
O
3
d)

 

Z  8 2  Cos  i.Sen  é uma das raízes
16
16 

a)
Z1  2(Cos40  i.Sen40 )



complexos: Z 2  3(Cos135  i.Sen135 )



Z 3  1(Cos125  i.Sen125 )
3  3.i
28. (FRANCO)
a)

a)
4
c)
argumentos formam uma P.A cuja razão é:
Uma circunferência de centro
Uma parábola.
Uma circunferência de centro
Uma elipse.
Uma circunferência de centro
O
5
b)
de
Z  16  16 3.i têm o mesmo módulo e seus
Z  2  i  5 , é:
25. (FRANCO)
6
29. (FRANCO)
24. (FRANCO)
O lugar geométrico descrito pelo
número complexo
Z  a  b.i , tal que
a)
b)
c)
d)
e)
 3 i
3.Z  i.Z  2  2i  0 é:
que
Sejam

d)
27. (FRANCO) O módulo do número complexo Z tal
a)
Z1 e Z 2 os números
Z1  3.Cos30  i.Sen30 
complexos
e


Z 2  5.Cos45  i.Sen45 . O produto de Z1
pôr Z 2 é o número complexo:
23. (FRANCO)
 3 i
 2 3  2i
c)
b) 
3 1
 i
2 2
GABARITO
1. A
7. E
13. D
19. B
25. B
2. D
8. A
14. B
20. B
26. D
3. B
9. C
15. C
21. D
27. E
4. A
10. A
16. B
22. E
28. B
5. E
11. C
17. A
23. E
29. E
6. E
12. C
18. A
24. C
30. E