Notas de aula até a última semana

4 Linhas de Transmissão em ressonância e Cavidades Ressonantes
4.1 Circuitos Ressonantes
Circuitos ressonantes são muito importantes para circuitos osciladores, amplificadores
sintonizados, filtros, medidores de freqüência, etc. Sua utilização vai desde alguns poucos hertz até
freqüências ópticas.
O ponto de partida para a análise destes circuitos é a revisão de circuitos RLC na
ressonância. A partir daí, serão analisados com detalhes a cavidade retangular e circular.
4.1.1 Circuito Ressonante RLC em série
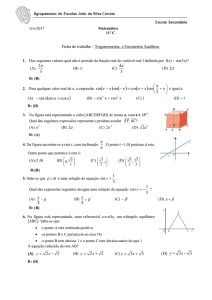
Inicialmente, determinemos a impedância de entrada do circuito RLC série
Figura 35 – Circuito RLC série
V
1
Z in  in  R  j..L 
I in
j..C
(4.1)
A potência entregue é dada por:
1
1
1
1 

Pin  .V .I *  .Z in . | I | 2  . | I | 2 . R  j..L  j.

2
2
2
..C 

(4.2)
A potência dissipada no resistor é dada por:
Pdiss 
1
. | I | 2 .R
2
(4.3)
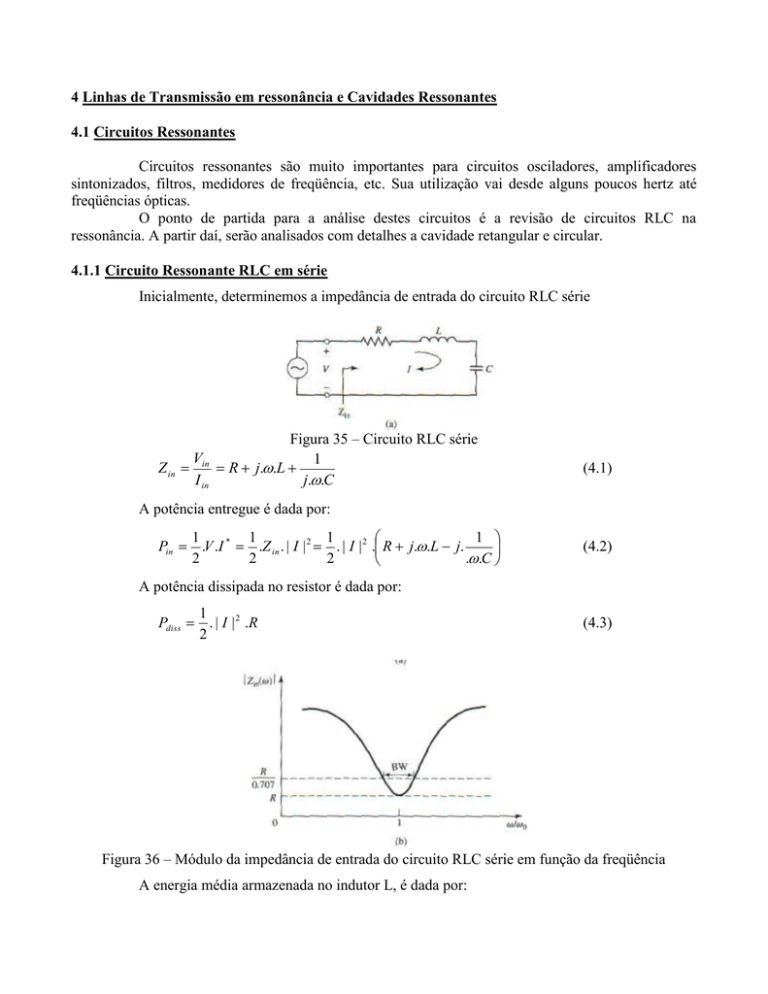
Figura 36 – Módulo da impedância de entrada do circuito RLC série em função da freqüência
A energia média armazenada no indutor L, é dada por:
1
Wm  . | I | 2 .L
4
(4.4)
E a energia média armazenada no capacitor é dada por:
1
1
1
We  . | Vc | 2 .C  . | I | 2 . 2
4
4
 .C
(4.5)
Nas equações (4.4) e (4.5) Vc e I são, respectivamente, os valores de pico da tensão sobre o
capacitor e da corrente no circuito.
A potência complexa pode ser escrita como:
Pin  Pd  2. j..Wm  We 
A impedância de entrada pode então ser escrita como:
Z in 
2.Pin Pdiss  2. j..Wm  We 

| I |2
| I |2
2
(4.6)
(4.7)
A ressonância ocorre quando Wm  We e nesta situação a impedância de entrada é tal que:
Pdiss
R
(4.8)
| I |2
R
Que é uma impedância puramente real e ocorre na freqüência  0 , dada por:
Z in 
0 
1
L.C
(4.9)
Um parâmetro importantíssimo de um circuito ressonante é o seu fator de qualidade Q, que
é definido como:
Q  .
Energia média armazenada
Potência dissipada
(4.10)
Ou, escrito de outra forma:
Q  .
Wm  We
Pd
(4.11)
Desta forma, o parâmetro Q é uma medida da perda de um circuito ressonante, ou seja,
baixas perdas implicam em um maior Q e vice-versa.
Assim, para um circuito ressonante em série, tem-se que:
1

2
 . | I } .L.2 
4
   0 .L  1
Q  0 . 
1
R
 0 .R.C
. | I | 2 .R
2
(4.12)
Esta expressão mostra que Q decai com o aumento de R. consideremos agora o que ocorre
próximo da freqüência de ressonância, onde   0   com  pequeno.
1 

Z in  R  j..L.1  2

  .L.C 
  2  0 2 

Z in  R  j..L.
2




(4.13)
.   0  




.
2




    0 


Z in  R  j..L.
  R  j..L.
  R  2. j. 
2
2






R.Q
 Z in  R  j.
.2.
0
De forma alternativa, um ressonador com perdas pode ser tratado com um ressonador sem
perdas cuja freqüência de ressonância é substituída por uma freqüência de ressonância efetiva
complexa dada por:

 0   0 .1 

j 

2.Q 
(4.14)
Demonstração:
A impedância de entrada para o caso sem perdas (R=0) é dada por:
Z in  j.2.L.  0 
(4.15)
Assim,
j. 0   0 .L


Z in  j.2.L.   0 
 j.2.L.   0   R  j.2.L.
2.Q 
Q

(4.16)
Este procedimento é útil para a maioria dos ressonadores onde as perdas são baixas. O fator
de qualidade pode ser determinado usando o método perturbacional. O Q é determinado supondo não
haver perdas e após as perdas são inseridas através de uma freqüência angular complexa.
Outro fator importante é a largura de faixa (BW) do ressonador. Quando a freqüência é tal
2
que | Z in |  2.R 2 , então a potência média entregue ao circuito é a metade da entregue na ressonância.
 BW

Tomando-se a BW fracional definida por
, tem-se que:
0
2
| R  j.R.Q.( BW ) | 2  2.R 2
BW 
(4.17)
1
Q
4.1.2 Circuito Ressonante RLC paralelo
Figura 37 – Circuito RLC paralelo
Neste caso, tem-se que a impedância de entrada é dada por:
1

1
Z in   
 j..C 
 R j..L

1
(4.18)
Cujo gráfico é dado por:
Figura 38 – Módulo da Impedância de entrada do circuito RLC paralelo em função da freqüência
A potência complexa é dada por:
1
1
1
1
Pin  .V .I *  .Z in . | I | 2  . | V | 2 . * 
2
2
2
Z in
1
j
1

 . | V |2  
 j..C 
2
 R .L

(4.19)
A potência dissipada pelo resistor é dada por:
1 | V |2
Pdiss  .
2 R
(4.20)
A energia armazenada no capacitor é escrita como:
We 
1
. | V | 2 .C
4
(4.21)
A energia armazenada no indutor é dada por:
1
1
1
Wm  . | I | 2 .L  . | V | 2 . 2
4
4
 .L
A potência complexa, pode então ser escrita como:
Pin  Pdiss  2. j..Wm  We 
(4.22)
(4.23)
Assim,
2.Pin Pdiss  2. j..Wm  We 

| I |2
| I |2
2
Na ressonância, tem-se que    0 e Wm  We e, portanto, tem-se que:
Z in 
Pdiss
R
| I |2
R
O fator de qualidade Q é dado por:
Z in 
Q  0 .
2.Wm
R

 0 .R.C
Pdiss 0 .L
(4.24)
(4.25)
(4.26)
Observa-se que, neste caso, à medida que R aumenta, o Q aumenta.
A análise próxima da ressonância pode ser feita simplificadamente usando o fato que:
1
 1  x  ....
1 x
Fazendo   0   , onde  é pequeno, tem-se que:
(4.27)



 1 1

0
Z in   
 j. 0 C  j..C 
j. 0 .L
R



1
1
1
1

j.
1

Z in    2  j..C     2. j..C 
R

 R  0 .L

R
R
Z in 


1  2. j..R.C
1  2. j.Q.
(4.28)
0
Sendo  0 
2
Z in 
1
, quando R = 0, tem-se que:
LC
1
2. j.C.   0 
(4.29)
Da mesma forma, o ressonador próximo da freqüência de ressonância, pode ser considerado
sem perdas, substituindo a freqüência ω0 pela freqüência complexa de acordo com a equação (4.14).
4.2 Fator de Qualidade carregado e descarregado
O Q definido anteriormente é uma característica própria do circuito ressonante, na ausência
de quaisquer efeitos de carregamento causados por circuitaria externa. Este Q é portanto chamado de Q
descarregado ou “unloaded Q”.
Na prática, há sempre um carregamento no circuito que irá causar uma variação no Q total.
Se a carga adicionar uma resistência RL, tal que:
Figura 39 – Circuito ressonante acoplado a uma carga externa RL
Tem-se que:
1
1
1


QL Qe Q
(4.30)
Na equação (4.30), QL é o fator de qualidade carregado e Qe é o fator de qualidade externo
dado por:
 0 .L
 R para circuitos em série
 L
Qe  
-1
  0 .L 
 R  para circuitos em paralelo
 L 
(4.31)
Q é o fator de qualidade sem carregamento.
4.3 Ressonância em linhas de transmissão
Para o estudo de linhas de transmissão na faixa de microondas, temos que usar o modelo de
parâmetros distribuídos.
O uso de curtos ou abertos em comprimentos pré-determinados é comum para a construção
de ressonadores. A partir do princípio quer estamos interessados no fator de qualidade de tais linhas,
devemos considerá-las com perdas.
4.3.1 Linha curto-circuitada de λ/2
Considerando um comprimento de uma linha de transmissão com perdas, curto-circuitada,
tal como mostra a figura abaixo:
Figura 40 – Linha de transmissão terminada em curto
Esta linha possui uma impedância Z0, uma constante de propagação β e uma constante de
2.
atenuação . Na freqüência ω = ω0, o comprimento elétrico é ℓ=λ/2 e  
. Da equação da

impedância complexa ao longo de uma linha de transmissão com perdas:
Z in  Z 0 .
Z L  j.Z 0 . tanh  . 
Z 0  j.Z L . tanh  . 
(4.32)
Como a linha é curto circuitada, ZL=0 e portanto a equação (4.32) reduz-se a:
Z in  Z 0 . tanh   j. .
Usando-se de propriedades trigonométricas, tem-se que:
(4.33)
Z in  Z 0 .
tanh  .   j. tan  . 
1  j. tanh  . . tan  . 
(4.34)
Na prática, a maioria das linhas de transmissão apresentam baixas perdas, tal que .  1 e,
portanto, tanh .  . . Se considerarmos   0   com  pequeno, tem-se para uma linha
operando no modo TEM:
 . 
.
vp

 0 .
vp


vp
(4.35)
Na equação (4.35) vp é a velocidade de fase. Se  
 .   
.

2
, tem-se que:
(4.36)
0
Portanto:

 .  .
. 
  tan 
 
tan  .   tan   


0
0 

 0 
(4.37)
Desta forma, substituindo s equações (4.36) e a aproximação obtida para tanh  . na
equação (4.34), podemos escrever a impedância de entrada da LT em curto de λ/2 como:
Z in  Z 0 .
 . 

 .  j.

 0 

 Z 0 . . 
 . 

. .
1  j.
 0 
 .
j.
 0



(4.38)
Comparando-se com a equação (4.13) da impedância de entrada para o circuito RLC série,
que é:
Z in  R  2. j.L.
(4.39)
Verifica-se, assim, que a LT em curto de λ/2 comporta-se como um circuito RLC série, tal
que:
R  Z 0 . .L
L
Z 0 .
2. 0
C
1
 0 2 .L
(4.40)
Desta forma, utilizando-se a equação (4.12) para o cálculo do fator de qualidade e
lembrando que ℓ = λ/2, tem-se que:
Z o .
 .L
2. 0
Q 0 

R
Z 0 . .
 0 .

.2 .


2

2 . 1
2. .
.
 2


2.
(4.41)
Exemplo 8 – Um ressonador de λ/2 terminado em curto é feito de uma linha de transmissão usando
cobre, com um condutor interno de 1 mm de raio e o externo de 4 mm de raio. Se a freqüência de
ressonância é 5 GHz, compare o Q de uma linha de transmissão preenchida com e ar e com Teflon (εr =
2,08) e δ = 0,0004. A condutividade do cobre é igual a 5,813.107 S/m
Solução – Para determinação do Q devemos calcular a atenuação devido às perdas metálicas e no
dielétrico (somente Teflon)
Para o Ar:
. 0
 1,84.10 2 
2.
Rs 
c 
Rs
 a
2. 0 . ln b
1 1
.    0,022 Np
m
a b
d  0
Teflon
c 
2.
 d  k0 .
0
Rs
2,08
r
2
 a
.. ln b
1 1
.    0,032 Np
m
a b
. tan    0,030 Np
m
Assim, para o ar tem-se que:
Qar 

104,7

 2380
2. 2.0,022
Para o teflon
Q
104,7. 2,08


 1218
2. 2.0,032  0,03
4.3.2 Linha de transmissão curto-circuitada de λ/4
Utilizando o resultado anterior, tem-se que para uma linha curto-circuitada de
comprimento ℓ, a impedância de entrada é dada pela equação (4.34). Escrevendo a tan  . como:
tan  .  
1
(4.42)
cot  . 
Substituindo-se a expressão (4.42) na equação (4.34) tem-se que:
Z in  Z 0 .
1  j. tanh  . . cot  . 
tanh  .   j. cot  . 
(4.43)
Se tomarmos ℓ = λ/4, para ω =ω0 e se consideramos   0   com  pequeno, tem-se
que:
 . 
0 . 
vp

.   .
 
vp
2
0
(4.44)
Assim, tem-se que:
   . 
  . 
 .
   tan 
  
cot  .   cot 
0 
0
2
 0 
(4.45)
Da mesma forma que no caso anterior, considerando-se baixas perdas, tem-se que:
tanh .  .
(4.46)
Substituindo as equações (4.45) e (4.46) na equação (4.43), tem-se que:
Z in 
Z0
(4.47)
 .
 .  j.
2. 0
Comparando-se a equação (4.47) com a da impedância de entrada do circuito RLC paralelo,
a equação (4.28), verificamos que a LT curto-circuitada de λ/4, comporta-se como um circuito RLC
paralelo. Portanto:
Z in(RLC paralelo) 
Z
R 0
 .
1
1
 2. j..C
R

C
4. 0 .Z 0
L
(4.48)
1
 0 2 .C
(Ressonânci a)
Assim:
Q   0 .R.C 
4.3.3 Linha aberta de λ/2



4. . 2.
(4.49)
Este circuito é bastante utilizado em ressonadores em “microstrip line” . Este tipo de
ressonador terá o comportamento de um circuito ressonante em paralelo.
Para uma LT de comprimento ℓ terminada em aberto, a impedância de entrada é dada por:
Z in  Z 0 .coth   j. .  Z 0 .
1  j. tan  . . tanh  . 
tanh  .   j. tan  . 
(4.50)
Considerando-se uma freqüência ω, tal que   0   com  pequeno, tem-se que:
 .   
 .
0
(4.51)

 .   .

tan  .   tan   
 0 
0

Considerando-se baixas perdas, tem-se que tanh .  . . Assim, substituindo-se esses
valores na equação (4.50), tem-se que:
Z in 
Z0
 .
 .  j.
 0
(4.52)



Por comparação, observa-se que LT aberta de λ/4 apresenta o comportamento de um
circuito RLC paralelo, tal que:
1
Z in(RLC paralelo) 
R
Z0
 .
1
 2. j..C
R
C

2. 0 .Z 0
L
(4.53)
1
 0 2 .C
(Ressonânci a)
E o fator de qualidade fica calculado como:
Q   0 .R.C 



2. . 2.
(4.54)
4.4 Cavidades Ressonantes
São constituídas quando o guia de ondas é fechado por paredes metálicas nas suas duas
extremidades.
Figura 41 – Cavidade ressonante retangular
Neste caso, tem-se que:

p.
d
(4.55)
Para o modo TE10, tem-se que:
  .x   p. .z 
E y  E0 . sin 
. sin 

 a   d 
j.E0  0    .x 
 p. .z 
Hy  
.
. sin 
. cos

  2.d   a 
 d 
Hz 
(4.56)
j.E0  0 
  .x   p. .z 
.
. cos
. sin 

  2.a 
 a   d 
Nas equações anteriores (4.55) e (4.56) o índice p indica o número de meias senóides ao
longo do guia.
4.4.1 Modos de ressonância

Modos TEm,n,p em guias retangulares
j. .k y . f
Ex 
.H 0 . cosk x .x . sin k y . y . sin k z .z 
kc . f c
Ey  
j. .k x . f
.H 0 . sin k x .x . cosk y . y . sin k z .z 
kc . f c
Hx  
k x .k z
Hy  
k y .k z
kc
kc
2
2
.H 0 . sin k x .x . cosk y . y . cosk z .z 
.H 0 . cosk x .x . sin k y . y . cosk z .z 
H z  H 0 . cosk x .x . cosk y . y . sin k z .z 
Nas equações (4.57), tem-se que k x 

Modos TEm,n,p em cavidades circulares:
m.
n.
p.
, ky 
e kz 
.
a
b
d
(4.57)
Er 
j.n. . f
.H 0 .J n k c .r . sin n. . sin k z .z 
k c .r. f c
E 
j. . f
'
.H 0 .J n k c .r . cosn. . sin k z .z 
fc
Hr 
kz
.H 0 .J n ' k c .r . cosn. . cosk z .z 
kc
n.k z
H  
2
k c .r
(4.58)
.H 0 .J n k c .r . sin n. . cosk z .z 
H z  H 0 .J n k c .r . cosn. . sin k z .z 
p' n
, que são as raízes ℓ ésimas da derivada da
a
função de Bessel ordinária de primeira espécie de ordem n. (n=0,1,2,3,....) e (ℓ=1,2,3,....).
Nas equações (4.58), tem-se que k c 

Modos TMm,n,p em guias retangulares
Ex  
k x .k z
Ey  
k y .k z
Hx 
2
kc
kc
2
.E 0 . cosk x .x . sin k y . y . sin k z .z 
.E 0 . sin k x .x . cosk y . y . sin k z .z 
j.. .k y
kc
Hy  
2
.E 0 . sin k x .x . cosk y . y . cosk z .z 
j.. .k x
kc
2
(4.59)
.E 0 . cosk x .x . sin k y . y . cosk z .z 
E z  E 0 . sin k x .x . sin k y . y . cosk z .z 

Modos TMm,n,p em guias circulares:
Er  
E 
kz
.E 0 .J n ' k c .r . cosn. . sin k z .z 
kc
n.k z
2
k c .r
.E 0 .J n k c .r . sin n. . sin k z .z 
Hr  
j.n. f
.E 0 .J n k c .r . sin n. . cosk z .z 
k c . .r. f c
H  
j. f
.E 0 .J n k c .r . cosn. . cosk z .z 
f c .
(4.60)
E z  E 0 .J n k c .r . cosn. . cosk z .z 
pn
, que são as raízes ℓ ésimas da função de Bessel
a
ordinária de primeira espécie de ordem n. (n=0,1,2,3,....) e (ℓ=1,2,3,....).
Nas equações (4.60), tem-se que k c 
4.5 Determinação das freqüências de ressonância
Como tem-se infinitos modos de ressonância, teoricamente, tem-se infinitas freqüências de
ressonância associadas. Porém, na prática, utilizamos as freqüências mais baixas.
Para determinar-se as freqüências de ressonâncias, utiliza-se o seguinte procedimento:
d  p.
g
2
p = 1,2,3,...
(4.61)
Portanto:
d  p.
0
 
1   0 
 c 
(4.62)
2
Na equação (4.62),  0 é o comprimento de onda ressonante. Assim, tem-se que:
 2.
 0 ..  
 0
2



2
(4.63)
k c   2   0 . .  k 2
2
2
Mas,
 m.   n. 
kc  
 

 a   b 
2. p.


g
d
Portanto:
2
2
2
0 
0 
(4.64)
 m.   n.   p. 
. 
 
 

.  a   b   d 
2
1
2
2
(4.65)
2
2
2
m n  p
     
 a  b d 
2
Esta expressão é válida para quaisquer modos TE ou TM no interior da cavidade. Para
cavidades circulares, tem-se que:
f0 
1
2. .a. .
. pn
2
 p. .a 


 d 
2
para modos TMn,ℓ,p
(4.66)
f0 
1
2. .a. .
 p. .a 

 para modos TEn,ℓ,p
 d 
2
. p' n
2
(4.67)
De acordo com as equações (4.66) e (4.67) podemos identificar a existência de modos
degenerados, ou seja, de mesma freqüência de ressonância, mas diferentes configurações de campos.
Podem ser exemplificados os modos TE e TM em cavidades retangulares cujos índices m, n e p sejam
iguais e em cavidades circulares, podem ser citados os modos TM111 e TE011.
Para cavidades retangulares, considerando b a menor dimensão, o modo TE101 é o
dominante com comprimento de onda ressonante dado por:
0 
2.a.d
(4.68)
a2  d 2
Para cavidades circulares, o modo TE011 é o que apresenta características que o tornam de
grande aplicação em ressoadores e freqüencímetros. O comprimento de onda ressonante é dado por:
0 
2.d
 2d 
1 

 1,64.a 
2
(4.69)
4.6 O Q de uma cavidade ressonante
Conforme definido pela equação (4.10) o fator que de uma qualidade é dado por:
Q  0 .
Warmazenada
Pdissipada
(4.70)
Para o cálculo da potência dissipada, devem ser levada em conta as perdas no condutor, bem
como as perdas no dielétrico, tal que:
1
1
1


Q Qc Qd
(4.71)
Na equação (4.71), Qc é o fator de qualidade levando em conta as perdas no condutor e Qd é
o fator de qualidade levando-se em conta as perdas no dielétrico. Para o cálculo do fator de qualidade
Qc, tem-se que:




Warmazenada  . | E | 2 .dV  . | H | 2 .dV
2V
2 V
E, de acordo com a equação (3.25), podemos escrever que:
(4.72)

Qc 
 0 .
Rs
| H |
| H
.dV Integrado no Volume 
V

.
2
t
| 2 .dS Integrado na Superfície interna da cavidade 
(4.73)
paredes
Exemplo 9 – Calcular o fator de qualidade Q de uma cavidade retangular operando no modo TE101
Solução – A energia armazenada é dada pela equação (4.72), tal que:

 . f
Wm  . | E y | 2 .dV 
2
 fc

  . f .H 0
Wm   .
 fc
2

 abd
 .H 0 2 .    sin 2 k x .x . sin 2 k z .z .dx.dy.dz 
2 0 0a

(4.74)
2
 a.b.d  . 2 a 3 .b.d
2
 .
 2 .
.H 0
8
2


Passemos para o cálculo da Potência dissipada, inicialmente determinando as componentes
tangenciais de campo.


2
Em x = 0 e em x = 0 | H z | 2  H 0 . sin 2 k z .z 


k 
2
| H x | 2   z  .H 0 . sin 2 k x .x . cos 2 k z .z 
Em y = 0 e y = b
k
 x
 2
2
| H z |  H 0 . cos 2 k x .x . sin 2 k z .z 


k 
2
Em z = 0 e z = d | H x |  z  H 0 . sin 2 k x .x 
 kx 
2
2
Assim, a potência dissipada é dada por:
2
 b d

a dk 
2
z
   cos k z .z .dy.dz      sin 2 k x .x . cos 2 k z .z .dx.dz 

0 0
0 0

 kx 
2 
Pd  Rs .H 0 .

2
2
a b k 
 a d  kz 

2
2
2
z
 0 0  k  cos k x .x . sin k z .z .dx.dz  0 0  k  sin k x .x .dx.dy 
 x
 x


Resolvendo-se a integral representada pela equação (4.75), tem-se finalmente que:
Pd 
Rs .a 2
b.b 1  a d 
2  a.b
.H 0 . 2  2  .  
2
2  d a 
a
d
(4.76)
(4.75)
Assim, utilizando-se a equação (4.73), tem-se que o fator de qualidade Q do cavidade é
dado por:
3

Wm
 . 
2.b. a 2  d 2 2
Q  0 .

.
Pd
4.Rs  a.d . a 2  d 2  2.b. a 3  d 3











(4.77)
Para uma cavidade cúbica, tem-se que:
Qcúbica  0,742

Rs
(4.78)
Para o cálculo do Q devido às perdas no dielétrico (Qd) é calculado levando-se em conta que
a energia elétrica média armazenada na cavidade é dada por:
We 
'
4

. | E | 2 .dV
(4.79)
V
A potência dissipada é calculada levando-se em condição a relação entre a condutividade do
dielétrico imperfeito e a parte complexa da permissividade, tal que:
 . ' ' 
1  
Pd  . J .E * .dV  0 . | E | 2 .dV
2V
2 V
(4.80)
O fator de qualidade é portanto é dado por:
Q  0 .
2.We  '
1


Pd
 ' ' tan  
Valores típicos de Q da cavidade variam entre 2000 a 100000.
5. Teoria Circuital para ondas guiadas
5.1 Modos TE/TM:
Guia Retangular (a>b)
(4.81)
y
 0,  0
b
a
x
Figura 42 – Geometria do guia de ondas retangular
Modo dominante TE10
  .x   j .  . z
H z  H 0 . cos
.e
 a 
 j.. 0 .a
  .x   j .  . z
Ey 
.H 0 . sin 
.e

 a 
Hx 
j. .a

(5.1)
  .x   j .  . z
.H 0 . sin 
.e
 a 
Tensão Equivalente
 
V   E.dl
(5.2)

V 
j.. 0 .a
  .x 
.H 0 .sin 
.  dy

 a y
x  0 V  0
a
x   V  Vmáx
2
(5.3)
(5.4)
Potência Complexa:


Et  x, y, z   e x, y . A  .e  j . . z  A  .e j . . z


H t  x, y, z   h  x, y . A  .e  j . . z  A  .e j . . z


(5.5)


e  x, y    j .  . z
Et  x, y , z  
.V .e
 V  .e j . . z 
C1


h  x, y    j .  . z
H t  x, y , z  
.I .e
 I  .e j . . z 
C2
(5.6)


Tensão e Corrente:
Na equação (5.6), C1 e C2 são constantes de proporcionalidade.
Uma vez que:


zˆ  e x, y 
ht x, y  
Z

(5.7)
Impedância de Onda
do modo no guia
Da teoria circuital:
V ( z )  V  .e  j . . z  V  .e  j . . z
I ( z )  I  .e  j . . z  I  .e  j . . z
Z0

Impedância
da linha

(5.8)
V V
 
I
I


Comparando-se as expressões para Et x, y, z  e H t x, y, z  , vem:
V V

A A
I
I
C2    
A
A
(5.9)
1 
Pin  . S .zˆ.dS
2S
(5.10)
C1 
Potência complexa incidente
onde:


  * 
S  Et  H t  e x, y . A  .e  j . . z  h x, y . A  .e  j . . z
| A |2   *
 Pin 
. e  h .zˆ.dS
2 S



*

Utilizando as equações (4.9), podemos reescrever a equação (5.11), tal que:


 *
V  .I 
Pin 
.
e
 h .zˆ.dS
*
2.C1.C2 S
Mas, da teoria circuital, tem-se que:
*
V  .I 
Pin 
2
(5.12)
*
(5.13)
Portanto, comparando-se as equações (5.12) e (5.13), tem-se que:
(5.11)


 
*
C1 .C2   e  h * .zˆ.dS
(5.14)
S
Linha de transmissão equivalente
V  C1 . A  C1 V 
Z0   


I
C2 . A C2 I 
(5.15)
C
Z0  1
C2
A impedância Z0 da linha de transmissão equivalente deve ser igual a impedância Zw do modo guiado,
ou seja:
Z0  Zw 
C1
C2
(5.16)
Exemplo 10:Determinar as expressões para as ondas de tensão e de corrente equivalentes para o modo
TE10:
Solução - As expressões para os campos são:
  .x   j .  . z
E y  A  .sin 
.e
 a 
Ey
A
  .x   j .  . z
Hx  

.sin 
.e
Z TE10
Z TE10
 a 
Potencia:
b
a
1 
1 | A  |2
  .x 
Pin  . S .zˆ.dS  .
. dy. sin 2 
.dx
2
2 ZTE10 0 0
 a 
 Pin 
| A |2 .b.a
4.Z TE10
Por outro lado
Ey 
V
  .x   j .  . z
. sin 
.e
C1
 a 
  .x 
sin 

I
a   j . . z

Hx 
.
.e
C2
Z TE10

Neste caso:
1 V  .I 
dy
  .x 
Pin  .
.
. sin 2 
.dx
* 
2 C1 .C2 0 Z TE10 0
 a 
*
b
a
Logo:
b
C1 .C 2  
*
0
C1 .C 2 
*
dy
  .x 
. sin 2 
.dx
Z TE1 0 0
 a 
a
b.a
2.Z TE1 0
Fazendo Z 0  Z w , tem-se que:
C1
 Z TE10
C2
Resolvendo para C1 e C2
C1 
a.b
2
C2 
1
Z TE10
.
a.b
2
Finalmente:
V   A  .C1  A  .
a.b
2
A
a.b
I  A .C 2 
.
Z TE10
2
Verificação:


V  .I 
| A |2 .a.b
Pin 

2
4.Z TE10
*
V ( z )  V  .e  j . . z  V  .e j . . z
I ( z )  I  .e  j . . z  I  .e j . . z
V V
   Z TE10
I
I
4.2 Matriz Espalhamento
Figura 43 – Junção a n acessos






V1  s11.V1  s12 .V2  s13 .V3  ...  S1n .Vn



V2  s 21.V1  s22 .V2  s23 .V3  ...  S 2 n .Vn

.
.
.
(5.17)




V3  sn1 .V1  s n 2 .V2  sn 3 .V3  ...  S nn .Vn

Ou matricialmente
V   S .V 


(5.18)
Pela definição tem-se que:
S11 
V1
V1





V2 V3 ... Vn 0


(5.19)
colocar carga casada nesses acessos
Propriedades
a) Reciprocidade
A matriz [S] é recíproca se [S]=[S]t
b) Sem perdas:
S . S *  I 
c) Recíproca e sem perdas
S . S *  I 
Exemplo 11: Uma junção a dois acessos é caracterizada pela seguinte matriz espalhamento:
0,3
0,790
0,2 
0,790
S   
Verifique se essa junção é recíproca e/ou sem perdas
Solução:
0,3
0,7  90
0,2 
0,7  90
0,3
0,790
 S  (Recíproca)
0,2 
0,790
S *  
S t  
0,3
0,790  0,3
0,7  90 
0,09  0,49
0,2190  0,14  90
.



  I 
0,2  0,7  90
0,2  0,21  90  0,1490
0,09  0,04
0,790

S . S *  
É recíproca, porém não é sem perdas.
Se colocarmos um curto na saída (acesso 2), qual será o coeficiente de reflexão?
Solução:
Figura 44 – Curto no término da saída de uma linha de transmissão.


V1  s11 .V1  s12 .V2



V2  s 21 .V1  s 22 .V2

Para o caso de curto, tem-se que:

V2  V2






 V2  s 21 .V1  s 22 .V 2  s 22 .V2  V2   s 21 .V1
V2



s .V
  21 1
1  s 22
s .s 




 
V1  s11 .V1  s12 .V2  V1  V1 . s11  12 21  
s 22  1 

 1 
V1
V1



s .s 
  s11  12 21  Para o caso 1  0,71 (não é um pois há perdas)
s 22  1 

Referências utilizadas:
1) Diniz, Aroldo B.; Freire, Gabriel F. O; “Ondas Eletromagnéticas”, LTC, 1973.
2) Pozar, David M. , “Microwave engineering”, 2nd edition, John Wiley , 1998.