Aula 31 - Funções Hiperbólicas

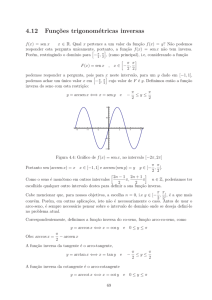
2. Função seno hiperbólico
UNIVERSIDADE DO ESTADO DE MATO GROSSO
CAMPUS UNIVERSITÁRIO DE SINOP
FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS
CURSO DE ENGENHARIA CIVIL
DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I
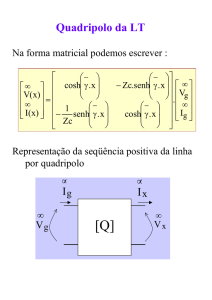
A função seno hiperbólico é definida por
senh x =
Funções Hiperbólicas
ex − e− x
2
O domínio e a imagem são o conjunto de todos
os números reais, cujo gráfico apresenta-se a seguir.
Prof.: Rogério Dias Dalla Riva
4
Funções hiperbólicas
2. Função seno hiperbólico
1.Introdução
senh x
2.Função seno hiperbólico
4
3.Função cosseno hiperbólico
3
4.Função tangente hiperbólica
2
5.Função cotangente hiperbólica
1
0
6.Função secante hiperbólica
-4
-3
-2
-1
0
1
2
3
4
-1
7.Função cossecante hiperbólica
-2
8.Outras funções hiperbólicas
-3
9.Identidades
-4
5
1. Introdução
3. Função cosseno hiperbólico
Certas combinações das funções exponenciais
A função cosseno hiperbólico é definida por
ex e e-x surgem frequentemente em matemática e
suas aplicações e, por isso, merecem nomes especiais.
Elas são análogas de muitas formas às funções
trigonométricas e possuem a mesma relação com a
hipérbole que as funções trigonométricas têm com o
círculo. Por essa razão são chamadas funções
hiperbólicas, particularmente seno hiperbólico,
cosseno hiperbólico e assim por diante.
O domínio é o conjunto de todos os números
reais e a imagem é o conjunto de todos os números no
intervalo [1, +∞), cujo gráfico apresenta-se a seguir.
3
6
cosh x =
ex + e− x
2
1
3. Função cosseno hiperbólico
5. Função cotangente hiperbólica
cosh x
A função cotangente hiperbólica é definida
4
por
3
cotgh x =
cosh x
e x + e−x
== x
senh x
e − e− x
2
O domínio é o conjunto ℜ - {0} e a imagem é o
conjunto de todos os números no intervalo
]-∞, -1[ U ]1, ∞[, cujo gráfico apresenta-se a seguir.
1
0
-4
-3
-2
-1
0
1
2
3
4
7
4. Função tangente hiperbólica
10
5. Função cotangente hiperbólica
cotgh x
A função tangente hiperbólica é definida por
tgh x =
8
6
−x
senh x e − e
=
cosh x e x + e − x
x
4
2
O domínio é o conjunto de todos os números
reais e a imagem é o conjunto de todos os números no
intervalo ]-1, 1[, cujo gráfico apresenta-se a seguir.
0
-3
-2
-1
0
1
2
3
-2
-4
-6
-8
8
4. Função tangente hiperbólica
6. Função secante hiperbólica
tgh x
A função secante hiperbólica é definida por
2
sech x =
1
-3
-2
-1
0
1
2
3
1
2
=
cosh x e x + e − x
O domínio é o conjunto dos números reais e a
imagem é o conjunto de todos os números no intervalo
]0, 1], cujo gráfico apresenta-se a seguir.
0
-4
11
4
-1
-2
9
12
2
6. Função secante hiperbólica
8. Outras funções hiperbólicas
sech x
As funções hiperbólicas também podem ser
reescritas em função de ex e e-x, como segue:
2,0
1,5
e x − e− x
e x + e− x
2
sech x = x
e + e− x
0,5
0,0
-4
-3
-2
-1
e x + e− x
e x − e− x
2
cossech x = x
e − e− x
tgh x =
1,0
0
1
2
3
4
-0,5
cotgh x =
-1,0
-1,5
-2,0
13
7. Função cossecante hiperbólica
16
9. Identidades
A função cossecante hiperbólica é definida
por
cossech x =
1
2
=
senh x e x − e − x
Existem identidades satisfeitas pelas funções
hiperbólicas que são similares àquelas satisfeitas
pelas funções trigonométricas, cujas demonstrações
encontram-se a seguir.
tgh x =
O domínio é o conjunto ℜ - {0} e a imagem é o
conjunto ℜ - {0}, cujo gráfico apresenta-se a seguir.
1
cotgh x
cosh2 x − senh2 x = 1
1 − tgh2 x = sech2 x
1 − cotgh2 x = −cossech2 x
14
7. Função cossecante hiperbólica
17
9. Identidades
cossech x
Como
5
tgh x =
4
3
senh x
cosh x
e cotgh x =
cosh x
senh x
2
decorre que
1
0
-4
-3
-2
-1
0
1
2
3
4
-1
tgh x =
1
cotg x
-2
-3
-4
-5
15
18
3
9. Identidades
9. Identidades
Em
Empregando as seguintes relações, obtidas das
definições de seno hiperbólico e cosseno hiperbólico
cosh2 x − senh2 x = 1
cosh x + senh x = e x
provamos a identidade substituindo pelas definições
de cosh x e senh x.
2
cosh x − senh x = e − x
pode-se provar as seguintes identidades:
senh( x + y ) = senh x ⋅ cosh y + cosh x ⋅ senh y
cosh( x + y ) = cosh x ⋅ cosh y + senh x ⋅ senh y
2
 e x + e− x   e x − e − x 
 e 2 x + 2e x e − x + e −2 x   e2 x − 2e x e − x + e −2 x 

 −
 =
−
=
2
2
4
4

 


 

e 2 x + 2e x e − x + e −2 x − e 2x + 2e x e − x − e −2 x
2e x e − x + 2e x e − x 2 + 2
=
=
=1
4
4
4
19
9. Identidades
22
9. Identidades
Em
Partindo
hiperbólico
1 − tgh x = sech x
2
2
da
definição
senh x =
provamos a identidade substituindo tgh x pela sua
definição em função de cosh x e senh x.
1−
função
e x − e− x
2
e x + y − e −( x + y ) 1 x y
= e ⋅ e − e− x ⋅ e− y
2
2
(
20
9. Identidades
seno
obtemos
senh ( x + y ) =
senh2 x cosh2 x − senh2 x
1
=
=
= sech2 x
cosh2 x
cosh2 x
cosh2 x
da
)
23
9. Identidades
Em
Entretanto
cosh x + senh x = e x
1 − cotgh x = −cossech x
2
2
cosh x − senh x = e − x
provamos a identidade substituindo cotgh x pela sua
definição em função de cosh x e senh x.
cosh2 x senh2 x − cosh2 x
cosh2 x − senh2 x
1−
=
=−
=
2
2
senh x
senh x
senh2 x
1
=−
= −cossech2 x
senh2 x
Assim sendo:
senh ( x + y ) =
senh ( x + y ) =
21
1 ( cosh x + senh x ) ⋅ ( cosh y + senh y ) − 


2 ( cosh x − senh x ) ⋅ ( cosh y − senh y ) 
1  cosh x ⋅ cosh y + cosh x ⋅ senh y + senh x ⋅ cosh y + senh x ⋅ senh y − 


2  cosh x ⋅ cosh y + cosh x ⋅ senh y + senh x ⋅ cosh y − senh x ⋅ senh y 


1
senh ( x + y ) = [2 ⋅ cosh x ⋅ senh y + 2 ⋅ senh x ⋅ cosh y ]
2
24
senh ( x + y ) = senh x ⋅ cosh y + cosh x ⋅ senh y
4
9. Identidades
Partindo
hiperbólico
da definição da função
cosh x =
cosseno
e x + e− x
2
obtemos
cosh ( x + y ) =
e x + y + e −( x + y ) 1 x y
= e ⋅ e + e − x ⋅ e− y
2
2
(
)
25
9. Identidades
Entretanto
cosh x + senh x = e x
cosh x − senh x = e − x
Assim sendo:
cosh ( x + y ) =
cosh ( x + y ) =
1 ( cosh x + senh x ) ⋅ ( cosh y + senh y ) + 


2 ( cosh x − senh x ) ⋅ ( cosh y − senh y ) 
1  cosh x ⋅ cosh y + cosh x ⋅ senh y + senh x ⋅ cosh y + senh x ⋅ senh y

2  cosh x ⋅ cosh y − cosh x ⋅ senh y − senh x ⋅ cosh y + senh x ⋅ senh y

1
cosh ( x + y ) = [ 2 ⋅ cosh x ⋅ cosh y + 2 ⋅ senh x ⋅ senh y ]
2
26
cosh ( x + y ) = cosh x ⋅ cosh y + senh x ⋅ senh y
+


5