x - Rei da Derivada

Lista 03
Teoria desta lista: funções
trigonométricas
inversas,
logaritmo, derivada logarítmica, funções exponenciais e
hiperbólicas.
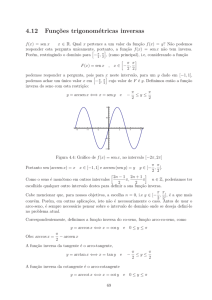
1.1. As funções trigonométricas inversas abaixo
foram obtidas considerando uma região do domínio
da função original. Indique qual a região adotada em
cada caso e calcule a derivada utilizando a seguinte
propriedade das funções inversas: y’(x)=1/x’(y).
Informe em qual domínio de x a derivada é válida:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
(ii)
y = x 2 ln x
(iii)
(iv)
(vi)
y = e 2 sen x
(vii)
y = ln sen x − e − x
(
)
(x)
y=
5
ln (ln ( x ))
1
+ 2−3 2+
3
3
1.3. Derive as funções abaixo utilizando a derivada
logarítmica (faça as considerações de domínio
que forem necessárias para aplicação do
logaritmo).
(ii)
y = 3x
(iii)
y = 2 sen x
(iv)
y = xx
cosseno
e x − e−x
e x + e−x
e cosh x =
.
2
2
senh x
cosh x
, cotgh x =
,
cosh x
senh x
1
1
sech x =
e cosech x =
cosh x
senh x
ln x
y = ln x ⋅ x + 1 + e 2−3 x
y = 3x
e
tgh x =
)
(ix)
(i)
sen x + x ln x + e − x
Calcule as derivadas dessas funções escrevendo o
resultado em termos de funções hiperbólicas.
y = xe x
(
x
Por conseqüência, são obtidas as outras funções
hiperbólicas:
(v)
e
y=x
senh x =
y = x 3 ln x 2
5
y=
ln (2 x − 1)
(viii) y = ln x + e
(vi)
2
seno hiperbólico
hiperbólico de x como sendo
1.2. Derive em relação a x:
y = x ln x
y = x sen
1.4. Define-se
y = arcsen x
y = arccos x
y = arctg x
y = arc cotg x
y = arcsec x
y = arc csc x
(i)
(v)
x
x
1