Quadripolo da LT

Quadripolo da LT
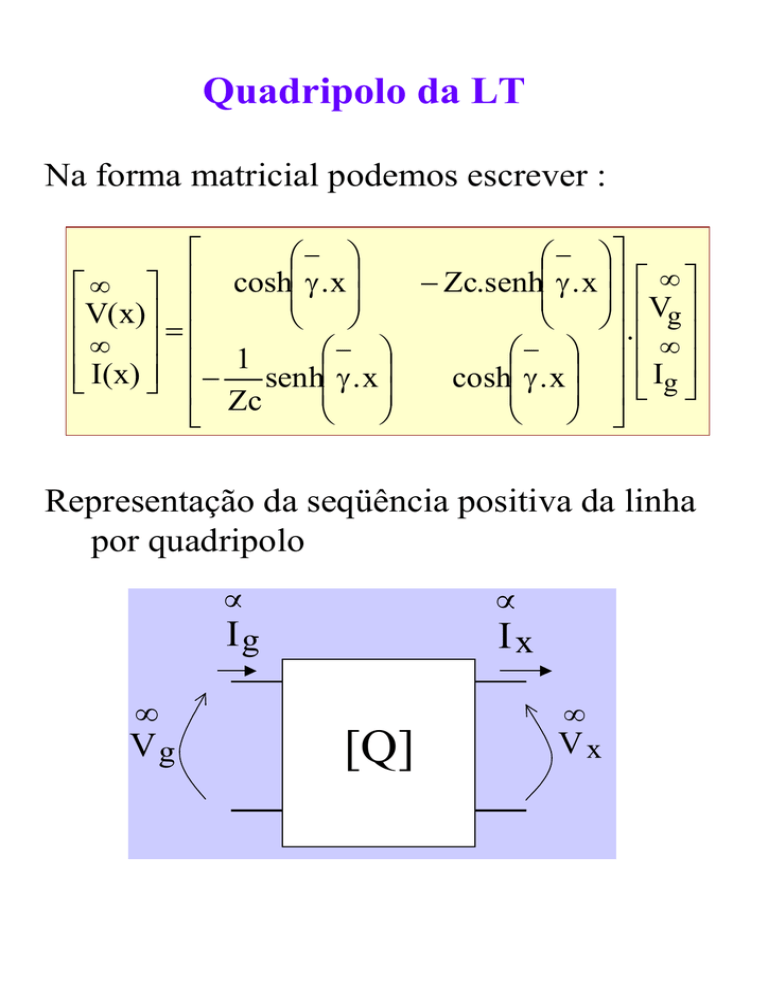
Na forma matricial podemos escrever :

− 
 − 
− Zc.senh γ . x   • 
 •   cosh γ . x 
  V 

V
(
x
)

=
 
  . g
•   1
− 
−  • 


 I(x)  − senh γ . x 
cosh γ . x    Ig 
 Zc
 
  
  
 

Representação da seqüência positiva da linha
por quadripolo
•
Vg
•
•
Ig
Ix
[Q]
•
Vx
Quadripolo em função das grandezas
na recepção

− 
 − 
 •   cosh γ .l0  Zc.senh γ .l0   • 




Vg  



 . Vrec
=
• 
 • 
−
−




 I   1 senh γ .l  cosh γ .l    Irec 
 g   Zc
 0
 0 

 



Modelo de quadripolo equivalente da
seqüência positiva da linha de transmissão,
definido pelas constantes A, B , C , D.
•
 • 
Vg  A B Vrec
. • 
 • =
 I  C D  Irec 
 g
Curto-Circuito na recepção
Para a linha em curto-circuito junto a recepção
podemos analisar as constantes ABCD do
quadripolo da linha.
•
Vrec = 0
•
•
−  •
Vg = B. Irec = Zc.senh γ .l0 . Irec




•
− 
Ig
= D = cosh γ .l0 
•


Irec


Esta relação é MUITO IMPORTANTE, pois
representa o ganho de corrente da linha em
curto (carga pesada).
Circuito aberto na recepção
Para a linha em vazio na recepção podemos
analisar as constantes ABCD do quadripolo
da linha.
•
Irec = 0
•
Vrec
1
=
•
− 
Vg
cosh γ .l0 




Esta relação é MUITO IMPORTANTE, pois
representa o ganho de tensão da linha em
vazio. Este aumento da tensão é conhecido
como EFEITO FERRANTI e o
analisaremos novamente mais adiante.
Aula 13
Modelo π equivalente
Normalmente representamos uma linha longa
através de um modelo formado por uma
impedância série e duas admitâncias
transversais.
Esta representação é utilizada para linhas
longas, mas pode ser aplicado a linha com
qualquer comprimento.
Os parâmetros são calculados para uma
determinada freqüência, sendo conhecido
como modelo π exato ou representação por
parâmetro distribuído.
Comparando π com o quadripolo
Vamos mostrar a seguir que o π exato é
equivalente à representação através de
quadripolo.
•
Ze
Ig (t )
•
I r (t)
•
•
V g (t)
Ye/2
Ye/2
V r (t )
equivalentes

− 
 − 
 •   cosh γ .l0  Zc.senh γ .l0   • 



 V
Vg  



 . r 
=
• 
•
−
−




 I   1 senh γ .l  cosh γ .l    I 
 g   Zc
 0
 0   r 



 

•
Ig (t )
I12
Ze=Z
•
I r (t)
I12
•
•
V g (t)
Ye/2=Ys
Ye/2
V r (t
hh
•
• − •
Ig = I12 + Y Vg
 •
• − •
• − •
 I12 = Ig − Y Vg = Ir + Y Vr

•
• −• −− •
•
• − •

Ir = I12 − Y Vr
 Vg = Vr + Z Ir + Z Y Vr
 •  − − • − •
•
• − •
 Vg = 1 + Z Y  Vr + Z Ir
Vg = Vr + Z I12






• • − • − − −  • − − •
Ig = Ir + Y Vr + Y1 + Z Y  Vr + Y Z Ir




• −
− − • 
− − •
Ig = Y 2 + Z Y  Vr + 1 + Y Z Ir








Quadripolo representativo da propagação:

− 
 − 
 •   cosh γ .l0  Zc.senh γ .l0   • 



 V
Vg  



 . r 
=
• 
•
−
−




 I   1 senh γ .l  cosh γ .l    I 
 g   Zc
 0
 0   r 



 

Quadripolo do π equivalente:
•
(
)
1
+
ZY
V

g
 =
 I•  Y (2 + ZY )
 g
•

Z  Vr 


.
•

(1+ ZY )  I 
 r
Comparando as duas matrizes e tendo em
conta a identidade:
γ l0
cosh γ l0 − 1
tanh
=
2
senh γ l0
Primeira identidade:
− 
Z = Zc.senh γ .l0 


Z=
1
2
1
2
1
2
1
2
z' z' l0
y' z' l0
− 
senh γ .l0 


Z = z ' l0 .
− 
 γ .l0 


− 
.senh γ .l0 


Segunda identidade:
(1+ ZY ) = cosh(γ l0 )
Substituido Z:
cosh(γ l0 ) −1
Y=
senh(γ l0 )
'
z l0
γ l0
γ l0 cosh(γ l0 ) −1
Y= '
z l0 senh(γ l0 )
γ l0
cosh γ l0 − 1
tanh
=
2
senh γ l0
Com:
1
'2
1
'2
1
'2
γ =z y
1
'2
1
'2
y z l0
γ l0 Y = y l0 tanh(γ l0 )
Y= '
tanh( )
1
2
z l0
2
z ' 2 l0
Y=
1
'2
1
'2
y y l0
1 1
'2 '2
y z l0
γ l0
Y = y l0
tanh(
'
γ l0
2
)
γ l0
tanh(
2
×
y
y
1
2
1
2
)

γ l0 
 tanh( ) 
Y y ' l0 
2 
Ysh = =
2
2  γ l0 


2


Modelo π hiperbólico – linha longa
•
Ze
I ger ( t )
•
I rec ( t )
•
•
V g (t)
Ye/2
Ye/2
V r (t )
Onde:
Ze – impedância série da
linha
Ye – admitância
transversal da linha
− 
senh γ l 
 
−
− 
 
Ze = Zcsenh γ l  = z' l
−
 
 
γl
− 
 γl 
l – comprimento da linha
tanh 
−
−
 
2


z’- impedância
Ye 1
γl
y' l
 
= tanh  =
−
longitudinal unitária
2 Zc
2 2
γl
 
y’- admitância
2
transversal unitária
Linhas médias
Os fatores
− 
senh γ l 
 
 
−
γl
e
− 
 γl 
tanh 
2
 
corrigem o
−
γl
2
circuito π da linha para incluir o efeito da
distância (propagação de onda). Quando estes
fatores são pequenos (tendem para unidade) a
linha pode ser representada somente como um
π nominal, ou seja, quando o tempo de trânsito
da onda for muito pequeno.
Esta representação é válida para linhas médias,
o que para a freqüência de 50- 60 Hz significa
na faixa de 80 a 240 km.
π nominal - Linha média
Para as linhas médias (80 a 240 km) deve ser
representada a impedância longitudinal e a
impedância transversal da linha sem a
correção do π hiperbólico.
•
z’ l
I ger ( t )
•
I rec ( t )
•
•
V g (t)
y’l/2
y’l/2
V r (t )
Linha curta
Para linhas com comprimento inferior a 80 km
a 60 Hz é razoável desprezar a admitância
transversal, representando somente a
impedância longitudinal.
•
I ger ( t )
z’ l
•
I rec ( t )
•
•
V g (t)
V r (t )
Modelo T nominal
Este modelo é aplicado para linhas médias,
mas não é muito utilizado.
•
I ger ( t )
•
V g (t)
z’ l/2
z’ l/2
y’ l
•
I rec ( t )
•
V r (t )
Associação em cascata de quadripolos
•
Ig
•
Vg
 A1
C
 1
B1 
D1 
•
•
I
Ir
•
V
A 2

 C2
B2 

D2 
•
Vr
Para o primeiro quadripolo
 •   − −  • 
Vg  A1 B1  V
 •  =  − −  • 
 I  C D   I 
1
 g  1
Para o segundo quadripolo
−  • 
•  −
V = A2 B2  Vr 
−  • 
•  −
 I  C2 D2   Ir 
O quadripolo total (produto dos quadripolos)
• − −  −
−  •
Vg  A1 B1  A2 B2  Vr 
×
 •  =  − − × −
−  •
 I  C D  C D   I 
1  2
2  r 
 g  1
Quadripolo de elemento em série
Em sistema de potência encontramos
elementos série como bancos de capacitores
série em linhas de alta tensão.
O modelo do quadripolo é idêntico ao da linha
curta, como apresentado a seguir.
•
I1
•
•
I2
−
Zs
•
V1
•
V2
•
  
 

V
V
1
Zs
1
• =
  •2 
 I  0 1   I 
 1
 2
−
Onde Zs corresponde à impedância do
elemento.
Quadripolo de elemento em derivação
Estes elementos podem representar cargas e
bancos de reatores e de capacitores para a
terra.
O modelo do quadripolo é semelhante ao do
modelo T, como apresentado a seguir.
•
I1
•
V1
•
I2
−
Yd
•
V2
•
•
V1 =  1− 0 V2 
 •  Yd 1  • 
  I 
 I1  
 2
Onde Yd corresponde à admitância do
elemento.
Efeito Ferranti
Elevação de tensão sustentada (regime
permanente) na extremidade aberta
de uma linha de transmissão, ou
seja, tensão na recepção em vazio
superior à tensão na geração.
Seja uma linha longa descrita pelo
quadripolo abaixo.

− 
 − 
 •   cosh γ .l0  Zc.senh γ .l0   • 



 V
Vg  

 . r 


=
• 
•
−
−




 I   1 senh γ .l  cosh γ .l    I 
 g   Zc
 0
 0   r 



 

Ganho de tensão da linha
No caso de linha aberta temos:
•
Ir
=0
•
−
•
Vg = Vr
cosh (γ l )
•
Vr
•
Vg
=
1
−
cosh (γ l )
EXERCÍCIO 1: Calcular os parâmetros
da LT e o modelo π – longo e nominal
(a) π longo da linha 400 km
(b) π nominal 400 km
(7.51, 36,00)
3.60 m
0.2 m
(9.27, 24,04)
0.2 m
•Linha Araraquara - Bauru; Jupiá - Ilha
Solteira (altura médias).
•Tensão base de 440 kV
•Linha transposta
Dados da LT
•Condutor de fase : cabo Grosbeak
–raio externo : 12,57 mm
–raio interno : 4,635 mm
–resistência CC : 0,089898 Ω/km
–temperatura : 75 °C
•cabos pára-raios : EHS 3/8″
–raio externo : 4,572 mm
–resistência CC : 4,188 Ω/km
–temperatura : 45 °C
•resistividade do solo : 2000 Ω.m
•comprimento da linha : 350 km
•flecha a meio vão
–fase : 13,43 m
–pára-raios : 6,4 m
•Freqüência : 60 Hz
Rint = Rcc = 0,089898 Ω / km
Z1 = Rint + j X1ext
µ0  DMG
1
Xext = ω ln

2 π  RMG
DMG = 3 dab .dac .dcb (distânciasaos centrosdos feixes)
DMG = 3 9,94.9,94.18,54 = 12,2357
RMG = 4 (R1. FC).da1a 2 .da1a3 .da1a 4
RMG = 4 (0,01257.0,952175).0,4.(0,4. 2 ).0,4
RMG = 0,181421
X1ext = 0,317524
Z1 = 0,0224745 + j 0,317524 Ω / km
 DMG
1
Y = jω2 π ε0 ln

RMG


−1
Y = j 4,99234µS/km
1
DMG = 3 dab .dac .dcb (distânciasaos centrosdos feixes)
DMG = 3 9,94.9,94.18,54 = 12,2357
RMG = 4 R1.da1a 2 .da1a3 .da1a 4 (dist. sub − condutores)
RMG = 4 0,01257.0,4.(0,4. 2 ).0,4
RMG = 0,183657
Calculando γ e Zc
−
γ=
−
γ=
− −
Z1 . Y1
(0,0224745 + j 0,317524)10−3. j 4,99234.10-9
−
γ = 4,453 .10−5 + 1,25983 10−3 [km-1]
Zc =
−
Z1
−
Y1
−
(0,0224745 + j 0,317524)10−3
−
Zc =
−
j 4,99234.10-9
Zc = 252,35 - 8,92 Ω ≈ 252 Ω
Pc = 768 MVA
Modulo π nominal
z ' = 0,022475 + j0,317524
y ' = j 4,9923
µS
Ω
km
km
Z c = 252,35 − j8.9197 ≈ 252 Ω
γ = 4,4530.10 −5 + j1,2598.10 −3 km −1
−
Zπnominal = z'l = 8,9898+ j127,01 Ω
−
−
Y y'l
Ysh = =
= j9,984.10−4 S
2 2
Modulo π longo
− 
senh γ l 
−
  = 8,2441+ j121,734 Ω
Z π −longo = z' l
−
γl
− 
γl

tanh 
2
−
y' l
  = j1,0201.10−3 S
Y sh _ π −longo =
−
2
γl
2
Exercício: Calcular Ganho de tensão
para a linha anterior em vazio
• L= 400 km
• Calcular ganho usando quadripolo para pi
longo;
• Calcular ganho usando o quadripolo do π
Ganhos de tensão para a linha
anterior em vazio

− 
 − 
 •   cosh γ .l0  Zc.senh γ .l0   • 



 V
Vg  



 . r 
=
• 
•
−
−




 I   1 senh γ .l  cosh γ .l    I 
 g   Zc
 0
 0   r 



 

•
gπ −longo =
Vr
•
Vg
=
1
−
cosh (γ l )
•
(
)
1
+
ZY
V

g
 =
 I•  Y (2 + ZY )
 g
= 1,1417
•

Z  Vr 


.
•

(1+ ZY )  I 
 r
•
g π − nominal =
Vr
•
Vg
1
1
= =
= 1,1452
A (1 + Z πno min alYπno min al )
Resultados 60 Hz
Transmissão em meio comprimento
de onda
Não há necessidade de compensação de
reativo
Ganho de tensão – 60 Hz
Comprimento
da linha [km]
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
Ganho
V2
V1
1,008262
1,033743
1,078675
1,147335
1,247122
1,390806
1,601388
1,923779
2,457539
3,472606
6,011501
17,03002
9,181355
4,368813
2,858087
Comprimento
da linha [km]
1600
1700
1800
1900
2000
2100
2200
2300
2400
2500
2600
2700
2800
2900
3000
Ganho
V2
V1
2,144737
1,737749
1,480409
1,307822
1,188521
1,105621
1,049479
1,014461
0,997392
0,996807
1,01263
1,046151
1,100293
1,180256
1,294836
Corrigindo o Efeito Ferranti
•
Ze
I ger ( t )
•
I rec ( t )
•
•
V g (t)
Ye/2
− 
senh γ l 
 
−
 
Ze = z' l
−
γl
Ye/2
V r (t )
− 
 γl 
tanh 
−
2
Ye y' l
 
=
−
2
2
γl
2
• Adicionar compensação reativa para
“consumir” os reativos “gerados” pela LT
em vazio.
• Objetivo => reduzir o comprimento elétrico
da linha (linha convencional).
EXERCÍCIO: Calcular
• Quadripolos da LT anterior para os dois
modelos
• Calcular o montante de reativo para
compensar 70 % da admitância transversal
• Calcular o Quadripolo da compensação
derivação
• Calcular Quadripolo total para os dois
modelos
• Ganhos de tensão após compensação
Quadripolos dos modelos Pi
Pi – longo:

− 
 − 


•
   cosh γ .l0
Zc.senh γ .l0   • 



 V
Vg  



 . r 
 • =
− 
−  •


1
 I   senh γ .l  cosh γ .l    I 
 g   Zc
 0
 0   r 




 
•
•
-3




V
0,876
+
j8,601.10
8.244
+
121,734
V
r
 g =

.
 •
 I•  
j1,913.10-3
0,874+ j8,601.10-3   I 
 r
 g
Pi – nominal:
•
Vg  =  (1 + ZY )
 I•  Y (2 + ZY )
 g
•

Z  Vr 
. • 

(1+ ZY )  I 
 r
•
•
-3




V
0,873
+
j8,976.10
8,9898
+
j1.27,020
Vr 
 g =

.
•
-3
-3 
 I•  
j1,870.10
0,873+ j8,976.10   I 
 r
 g
Quadripolo da compensação
Cálculo da compensação em derivação
A admitância do quadripolo de compensação é calculada sabendo
a porcentagem de compensação (pc). Normalmente a
compensação shunt é feita nos extremos da LT (metade da
compensação total para cada lado):
pc
Yc = −(
) ( jYsh )
100
Pi – longo:
− 
γl
tanh 
2
 pc  y' l
 
Yc = − j

−
 100  2
γl
2
Quadripolo pi - longo
1
0

QCπ−longo = 

-4
j7,141.10
1


Quadripolo pi - nominal
 pc  y' l
Yc = − j

 100  2
1
0

QCπ−nominal = 

-4
j7,1408.10
1


Quadripolo total e ganhos
Pi – longo:
[QT
π−longo
] = [QC
π−longo
][Q
π−longo
][QC
π−longo
]
0,962+ j 2,580.10-3 8,244+ j121,734 
QTπ−longo = 
-4
-3 
0,962+ j 2,580.10 
 - j6,007i.10
Ganhoπ−longo = 1,03868870339832
Pi - nominal
0,962+ j 2,416.10-3 8,989+ j127,001 
QTπ−nominal = 
-4
-3 
0,962+ j 2,416.10 
 - j5,5849i.10
Ganhoπ−nominal = 1,03748059467647
Admitância transversal e
compensação em derivação
Comprimento
[km]
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
1600
1700
1800
1900
2000
2100
2200
2300
2400
2500
2600
2700
2800
2900
3000
Y [µS]
Linha
curta
456,547
913,094
1369,641
1826,188
2282,735
2739,282
3195,829
3652,376
4108,923
4565,47
5022,017
5478,564
5935,111
6391,658
6848,205
7304,752
7761,299
8217,846
8674,393
9130,94
9587,487
10044,03
10500,58
10957,13
11413,68
11870,22
12326,77
12783,32
13239,86
13696,41
Y [µS]
Linha
longa
459,0609
933,6103
1441,29
2004,715
2655,998
3445,131
4457,42
5854,535
7987,36
11781,29
20521,97
35382,4
-27943,7
-14561,6
-9345,65
-6669,98
-5015,02
-3862,48
-2990,35
-2287,62
-1691,98
-1165,01
-680,832
-220,295
232,3671
691,7835
1173,35
1695,308
2281,591
2966,388
Reativo
Reativo
derivação derivação
[Mvar]
[Mvar]
Linha
Linha
curta
longa
88,3875 88,87419
176,775
180,747
265,1625 279,0338
353,55 388,1128
441,9375 514,2012
530,325 666,9774
618,7125 862,9566
707,1 1133,438
795,4875 1546,353
883,875 2280,857
972,2625 3973,054
1060,65 6850,032
1149,037 -5409,91
1237,425 -2819,13
1325,812 -1809,32
1414,2 -1291,31
1502,587 -970,908
1590,975 -747,775
1679,362 -578,932
1767,75 -442,883
1856,137 -327,566
1944,525 -225,546
2032,912 -131,809
2121,3 -42,6491
2209,687 44,98628
2298,075 133,9293
2386,462 227,1606
2474,85 328,2115
2563,237 441,7159
2651,625 574,2927
Ganho para compensação em
derivação
Comprimento
Ganho
Ganho
Ganho
Ganho
Ganho
[km]
LT sem comp. Comp. 70 % Comp. 80 % Comp. 90 % Comp. 100 %
100
1,008262
1,002464
1,001642
1,00082
1
150
1,01875
1,005552
1,003695
1,001844
1
200
1,033743
1,009889
1,006571
1,003274
0,999999
250
1,053567
1,015489
1,010273
1,005109
0,999998
300
1,078675
1,02237
1,014802
1,007345
0,999996
350
1,109668
1,030555
1,020163
1,009977
0,999993
400
1,147335
1,040068
1,026357
1,013001
0,999989
450
1,192703
1,05094
1,033388
1,016411
0,999982
500
1,247122
1,063204
1,041259
1,020199
0,999973
550
1,312366
1,076898
1,049972
1,024358
0,999961
600
1,390806
1,092063
1,059531
1,028878
0,999946
650
1,485661
1,108744
1,069937
1,03375
0,999927
700
1,601388
1,126988
1,081189
1,038961
0,999903
750
1,744326
1,146845
1,093287
1,044499
0,999874
800
1,923779
1,16837
1,106227
1,05035
0,999839
850
2,15394
1,191615
1,120004
1,056499
0,999799
900
2,457539
1,216638
1,13461
1,062927
0,999752
950
2,873289
1,243495
1,150032
1,069617
0,999698
1000
3,472606
1,272239
1,166256
1,076547
0,999637
1050
4,402186
1,302923
1,183259
1,083697
0,999568
1100
6,011501
1,335595
1,201017
1,091041
0,999492
1150
9,312455
1,370295
1,219497
1,098554
0,999407
1200
17,03002
1,407054
1,238659
1,106208
0,999315
Efeito Ferranti Linha
compensada
Reativo Total
Comprimento Reator 70 % Reator 80 % Reator 90 % Reator 100 %
[km]
[Mvar]
[Mvar]
[Mvar]
[Mvar]
100
61,956
70,80686
79,65772
88,50857
150
93,0935
106,3926
119,6916
132,9907
200
124,4239
142,1987
159,9735
177,7484
250
156,0139
178,3016
200,5892
222,8769
300
187,9324
214,7799
241,6274
268,4749
350
220,2513
251,7158
283,1803
314,6447
400
253,0457
289,1951
325,3445
361,4939
450
286,3951
327,3086
368,2222
409,1358
500
320,3837
366,1528
411,9219
457,691
550
355,102
405,8309
456,5598
507,2886
600
390,6473
446,454
502,2608
558,0676
650
427,1249
488,1427
549,1606
610,1784
700
464,6497
531,0283
597,4068
663,7853
750
503,3478
575,2546
647,1615
719,0683
800
543,358
620,9805
698,6031
776,2256
850
584,8341
668,3819
751,9296
835,4773
900
627,9479
717,6548
807,3616
897,0685
950
672,8916
769,019
865,1463
961,2737
1000
719,8817
822,722
925,5622
1028,402
1050
769,1638
879,0443
988,9248
1098,805
1100
821,0172
938,3054
1055,594
1172,882
1150
875,7623
1000,871
1125,98
1251,089
1200
933,7683
1067,164
1200,559
1333,955
Impedância Longitudinal e
compensação série
Comprimento
X [Ω]
[km]
Linha curta
35,9458
100
200
71,8916
300 107,8374
400 143,7832
500
179,729
600 215,6748
700 251,6206
800 287,5664
900 323,5122
1000
359,458
1100 395,4038
1200 431,3496
1300 467,2954
1400 503,2412
1500
539,187
1600 575,1328
1700 611,0786
1800 647,0244
1900 682,9702
2000
718,916
2100 754,8618
2200 790,8076
2300 826,7534
2400 862,6992
2500
898,645
2600 934,5908
2700 970,5366
2800 1006,482
2900 1042,428
3000 1078,374
Reativo série Reativo série
[Mvar]
[Mvar]
X [Ω]
Linha longa Linha curta
Linha longa
35,84796
71,11077
105,2128
137,5973
167,7354
195,1348
897,6478
992,1345
219,3478
769,4124
882,6166
239,9783
673,2358
806,7395
256,6888
598,4318
754,2208
269,2052
538,5887
719,1541
277,3219
489,626
698,1057
280,9049
448,8239
689,2012
279,894
414,299
691,6904
274,3037
384,7062
705,7869
264,2234
359,0591
732,7134
249,8153
336,6179
774,9725
231,3126
316,8169
836,9627
209,0151
299,2159
926,2491
183,2846
283,4677
1056,281
154,5393
269,2943
1252,756
123,2465
256,4708
1570,836
89,91552
244,813
2153,132
55,08916
234,169
3514,303
19,33501
224,4119
10012,92
-16,7638
215,4355
-11548,7
-52,618
207,1495
-3679,35
-87,6418
199,4773
-2208,99
-121,263
192,3531
-1596,53
-152,93
185,7202
-1265,94
-182,125
179,5296
-1063,01
Exercício 2 – LT 345 kV
12,5 m
4
1
8,50 m
0,457 m
2
8,50 m
3,44 m 3,7 m
5
3
30,5 m
2,2 m
0,45 m
Calcule o montante de reativo a instalar para
compensar 80 % da admitância transversal
da linha. Calcule o ganho da tensão sem e
com a compensação. Comprimento da linha:
320 km. Instale a compensação junto aos
extremos da linha.
Dados
Dados cabos fase
Dados cabo PR
Diâmetro
0,02959 m
externo Diâmetro
0,009144 m
Diâmetro
0,00739 m
interno Rcc – 4,188 Ω/km
Rcc – 0,0509 Ω/km
µr – 1
externo
µr - 70
Flecha PR - 6,4 m
Flecha φ − 13,43 m
Dados do solo
Resistividade – 2000 Ω.m
Cálculo do quadripolo LT
RMG = 0,08223 m
DMG = 10,7093 m
z ' = 0,02545 + j0,367
y ' = j 4,3002
µS
Ω
km
km
Z c = 292,37 - j10,1212 ≈ 292 Ω
γ = 4,352.10 −5 + j1,2573.10 −3 km −1
Pi – longo:

− 
 − 


•
   cosh γ .l0
Zc.senh γ .l0   • 



 V
Vg  



 . r 
 • =
− 
−  •


1
 I   senh γ .l  cosh γ .l    I 
 g   Zc
 0
 0   r 




 
•
•
-3




V
0,9202
+
j5,453.10
7,7104
+
j114,3604
V
r
 g =

.
 •
 I•  
j1,3392.10-3
0,9202+ j5,453.10-3   I 
 r
 g
ganho= 1,08664926597490
Cálculo do quadripolo LT +
compensação
Quadripolo do compensador:
1
0

QCπ−longo = 

-4
j6,488217
1


− 
γl
tanh 
2
 pc  y' l
 
Yc = − j

−
 100 2
γl
2
Quadripolo total:
0,97607+ j1,636.10-3

7,7104+ j114,36

-4
-3 
j4,13466.10
0,97652+ j0,97607+ j1,636.10 

ganho= 1,02451189396227
Exemplo 3 – LT 765 kV
Calcule o montante de reativo a instalar para
compensar 70 % da admitância transversal
da linha e 45 % da impedância
longitudinal da linha. Calcule o ganho da
tensão antes e depois da compensação.
Comprimento da linha : 500 km. Instale a
compensação série no meio da linha e a
compensação em derivação junto aos
extremos da linha e junto da compensação
série.
Dados cabos fase
Raio externo – 0,016 m
Raio interno – 0,004 m
Rcc – 0,0509 Ω/km
µr - 1
Dados cabo PR
Raio externo – 4,572 mm
Rcc – 4,188 Ω/km
µr - 70
Dados do solo
Resistividade – 2000 Ω.m
Silhueta
28,0 m
a
b
Altura média =altura torre – 2/3 flecha
hPRmédio – 55,8 m
0,457 m
14,34 m
hφmédio – 42,34 m
0,457 m
14,34 m
c
Aula 14
Fluxo de potência em
linhas de transmissão
trifásicas equilibradas
SISTEMAS DE ENERGIA
ELÉTRICA I
• Bibliografia
– Introdução a Sistema de Energia
Elétrica – Alcir Monticelli e
Ariovaldo Garcia
– Power System Analysis – Hadi
Saadat
– Elementos de Análise de Sistema
de Potência – Willian Stevenson
– Fundamentos de Sistemas
Elétricos de Potência - Luiz Cera
Zanetta Junior
– http://www.dsee.fee.unicamp.br/
%7Eccastro/cursos/et720/et720.ht
ml
Matriz admitância do modelo π
A matriz de admitância associada à
representação de quadripolo utilizada para a
linha de transmissão é diferente. Na matriz de
admitância as correntes nos terminais entram
na linha.
•
•
Yse
Ig (t )
I r (t)
•
•
V g (t)
Yder
V r (t )
Yder
As equações que descrevem o modelo são :
•
−
•
−
•
•
−
•
−
•
•
I r = Y der . V r + Y se .[ V r − V g ]
•
I g = Y der . V g + Yse .[ V g − V r ]
Na forma matricial temos:
−
•   −
 I r  = Y der + Yse
−
•  
 I g   − Yse
 • 
− Yse   V r 
.
−
−  • 
Y der + Yse  V g 
−
Onde a matriz de coeficientes é chamada de
matriz admitância da linha.
É importante lembrar que esta matriz de
admitância é formada pela impedância
longitudinal (hiperbólica) de seqüência
positiva da linha e pela admitância transversal
(hiperbólica) de seqüência positiva da linha.
Montagem da matriz:
•Termo diagonal : soma das admitâncias que
chegam ao nó.
•Termo entre nós i e k: negativo da admitância
entre os nós nós i e k.
Matriz admitância de uma rede
Vamos generalizar e obter a matriz de
admitância de uma rede formada somente por
linhas de transmissão.
3
1
I34
I43
2
4
Descrevendo a linha de transmissão 3-4 temos
−
−

•   34
34
Y
+
Y
se
 I34  =  der
•  
−
 I 43   − Y34
se

−
 •

34  
− Yse
 .  V3 
−
−  • 
34
34   V 4 
Yder + Yse 
Matriz admitância de uma linha
Genericamente temos :
−
−

•   km
km
Y
+
Y
se
 I km  =  der
−
•  
 I mk   − Y km
se

−
 •

km  
− Yse
 .  Vk 
−
−  • 
km
km   V m 
Yder
+ Yse

Aplicando a lei dos nós à rede temos :
•
•
•
I1 = I12 + I13
•
•
•
I 2 = I 21 + I 24
•
•
•
I3 = I31 + I34
•
•
•
I 4 = I 42 + I 43
Como as linha têm admitância para a terra não
nula, então :
• •
• •
I1 + I 2 + I3 + I 4 ≠ 0
Ou seja, as equações nodais acima são
independentes.
Substituindo as correntes dadas pelos modelos
πs das linhas temos :
−  •
− •
−  •
− •
 −
 −
•
 12
 13
12 
12
13 
13
I1 =  Yder
+ Yse
.
V
−
Y
.
V
+
Y
+
Y
.
V
−
Y
1
2
1
se
se 
se . V 3

 der








−  •
− •
−  •
− •
 −
 −
•
 12
 24
12 
12
24 
24
I 2 =  Yder
+ Yse
.
V
−
Y
.
V
+
Y
+
Y
.
V
−
Y
2
1
2
se
se 
se . V 4

 der








−  •
− •
−  •
− •
 −
 −
 13
 34
13 
13
34 
34
I3 =  Yder
+ Yse
.
V
−
Y
.
V
+
Y
+
Y
.
V
−
Y
3
1
3
se
se 
se . V 4

 der








−  •
− •
−  •
− •
 −
 −
•
 24
 34
24 
24
34 
34
I 4 =  Yder
+ Yse
.
V
−
Y
.
V
+
Y
+
Y
.
V
−
Y
4
2
4
se
se 
se . V 3

 der








•
Na forma matricial
•   −   • 
 I  = Y  . V 
     
Sendo a matriz de admitância de uma rede
dada por
−
−
−
−
12
12
13
13
Yder + Yse + Yder + Yse
−
12
− Yse
−
13
− Yse
0
−
12
− Yse
−
−
−
−
12
12
24
24
Yder + Yse + Yder + Yse
0
−
24
− Yse
−
13
− Yse
0
−
−
−
−
13
13
34
34
Yder + Yse + Yder + Yse
−
34
− Yse
0
−
24
− Yse
−
34
− Yse
−
−
−
−
24
24
34
34
Yder + Yse + Yder + Yse
Novamente temos - Montagem da matriz:
•Termo diagonal : soma das admitâncias que
chegam ao nó.
•Termo entre nós i e k : negativo da
admitância entre os nós nós i e k.
Atenção
Se os elementos em derivação forem nulos a
matriz de admitância passa a ser singular, pois
• •
• •
I1 + I 2 + I3 + I 4 = 0
Reparem também que a matriz admitância é
uma matriz com vários elementos nulos, o que
chamamos de alta esparsidade.
Define-se por grau de esparsidade a relação
entre o número de elementos nulos da matriz
pelo número total de elementos de uma matriz,
ou seja :
N elemento − nulo
G esparcidade =
N total − elemento
Os programas computacionais aproveitam esta
características para reduzir o espaço de
armazenamento das matrizes e manipular
matrizes menores.
Exemplo esparcidade
Considerando que em média uma rede possui
duas linhas ligadas a cada barra, calcule o grau
de esparsidade de uma matriz admitância de
uma rede com 1000 barras.
Temos matriz 1000 X 1000 com cada barra
com 2 linhas.
Elementos não nulos :
diagonal −1000
fora diagonal − 2 . 1000
total − 3000
Grau de esparsidade :
(1000 . 1000) − 3000
G=
100 = 99,7 %
1000 . 1000
Fluxo de potência em uma linha
Seja o diagrama simplificado da linha com a
convenção de sinais adotada apresentado a
seguir :
k
Ek
Em
Pkm
Pmk
Qkm
Qmk
m
O modelo π para deduzir as expressões dos
fluxos de potência ativa e reativa da linha é :
Ek
k
rkm + j xkm
Em
Ikm
j ykm
j ykm
m
Potência ativa e reativa da linha
Vamos obter as potências ativa e reativa da
linha em função das tensões das barras
terminais (fasor => amplitude e ângulo).
A impedância série é dada por :
rkm + j x km
Ou, escrevendo através de admitância série :
km
= g km + j bkm
y ser
onde
g km
rkm
= 2
2
rkm + x km
− xkm
bkm = 2
rkm + x 2km
A admitância transversal é dada por :
km
Yder
km
km
j yder = j b der = j
2
Sejam as tensões complexas nas barras
terminais dadas por :
•
E k = Vk e
•
jθ k
E m = Vm e
jθ m
A corrente injetada no terminal k tem duas
componentes e é descrito por :
•der •se
•
•
• 
der
se 
I km = I km + I km = jb km . E k + Ykm E k − E m 


•

ou seja
•
•
•
• 



(
)
I km = jb der
.
E
+
g
+
jb
E
−
E
k
k
m
km
km 
km




A potência complexa injetada no nó k é dada
por :
•*
Skm = Pk + j Q k = E k . I km
−
•
Logo
•
Pkm − j Q km = Vk e − jθ k I km
Lembrando que
π

π

cos − θ  = sen θ e sen  − θ  = cos θ
2

2

Chegamos a
Pkm = Vk2g km − Vk Vm g km cos θkm − Vk Vm b km sen θkm
(
)
Q km = − Vk2 b de
km + b km − Vk Vm g km sen θkm + Vk Vm b km cos θkm
Potência que entra no outro terminal
2g
Pmk = Vm
km − Vk Vm g km cos θ km + Vk Vm b km sen θ km
(
)
2 de
Q mk = − Vm
b km + b km + Vk Vm g km sen θkm + Vk Vm b km cos θkm
Perdas ativa e reativa na linha
As perdas ativas na linha são dadas por :
(
2
Pkm + Pmk = g km Vk2 + Vm
− 2Vk Vm cos θkm
ou
•
)
2
•
Pkm + Pmk = g km . E k − E m
Perda somente na resistência série.
E as perdas reativas por :
(
)
(
)
(
2 de
2
Q km + Q mk = − Vk2 + Vm
b km − b km Vk2 + Vm
− 2Vk Vm cos θkm
ou
•
•
2
2 b de − b
Q km + Q mk = − Vk2 + Vm
km . E k − E m
km
Perda reativa na reatância série e na
admitância transversal.
Lembrando que
cos A cos B + sen A sen B = cos( A − B)
)
Analisando a perda reativa na
linha
Reparem que a perda reativa na linha tem uma
parcela devido à perda no elemento
longitudinal e outra devido ao elemento
transversal.
Quando estas parcelas são próximas o
consumo de reativo da linha tende a zero.
Quando compensamos somente a admitância
transversal a linha continua consumindo
reativo devido à reatância longitudinal.
Exercício
Um gerador é conectado a uma carga por uma
linha de transmissão com um condutor por
fase. Os parâmetros de seqüência positiva da
linha são: C = 2,91x10-8 F/km, L = 1,72x10-8
H/km. A linha tem comprimento total de
100km. As tensões trifásicas na carga são
equilibradas com tensões de linha 230 kVef. A
potência consumida pela carga é 50 MVA
com fator de potência 0,8 atrasado. Determine
corrente e tensões no terminal gerador e as
perdas na linha de transmissão.
Cálculo da corrente e tensão na
carga e no gerador
Dados da linha:
z = 9.10 −2 + j0,648 Ω y = j1,097.10-5 S
L
= 243,12 Ω
C
γ ⋅ l = 1,841.10 − 2 + j0,2664-3
Zc =
Na Carga:
S21 = 50∠36,87° = 40 + j37,5 MVA
S21-1φ = 16,67∠36,87° MVA
Assumindo Tensão nominal na Carga:
230
V2 ft = VR =
∠0° = 137,79 kV
3
*
 S21−1φ 
 = 125,51∠ - 36,87° A
I 21 = I R = 
V 
 2-1φ 
Cálculo da tensão e correntes no Gerador:

− 
 − 
 •   cosh γ .l0  Zc.senh γ .l0   • 



 V
Vg  



 . r 
=
• 
•
−
−




 I   1 senh γ .l  cosh γ .l    I 
 g   Zc
 0
 0   r 



 

Tensão e corrente no gerador
•
• 
−3



V
+
+
0
,
9648
j
4
,
3186
.
10
4
,
3186
j
64
,
016
V
g
 =
.  •r 
•
−3
−3 
I  
j1,083.10
0,9648+ j 4,3186.10   I 
g
 r
 
 •  138359,96∠2,80°

Vg  = 
 I•   124,07∠38,40° 
 g
Tensão de linha no Gerador:
•
Vg linha = 239,61∠2,80 V
Potências e perdas na linha:
•
•
S12-3φ = 3 ⋅ V g ⋅ I12 = 41,87 − j29,98 MVA
*
Pperdas = 1,87 MW
Q perdas = 7,52 MW
Exercício
Uma linha trifásica de 100 km dada a seguir
pode ser considerada transposta. Esta linha
alimenta uma carga trifásica equilibrada de
200 MVA fp 0,8 atrasado. A tensão nominal
da linha é 345 kV. Freqüência do sistema : 60
Hz
•Determine a potência consumida na linha e a
tensão de linha junto a fonte.
2,2 m
12,5 m
4
8,50 m
2
8,50 m
3,44 m 3,7 m
5
3
30,5 m
1
0,45 m
LT 345 kV
0,457 m
Dados cabos fase
Dados cabo PR
Diâmetro externo 0,02959 m Diâmetro externo 0,009144 m
Diâmetro interno 0,00739 m Rcc – 4,188 Ω/km
Rcc – 0,0594 Ω/km
µr – 1
Flecha φ − 13,43 m
µr - 70
Flecha PR - 6,4 m
Dados do solo
Resistividade – 2000 Ω.m
Parâmetros unitários de seqüência
positiva
−
µ0  DMG 
Z1 = R int + jω
ln 
2 π  RMG 
−
3 8,5.8,5.17

0,0594
µ0 

Z1 =
+ jω
ln 
2
2 π  0,077709 . 0,014795. 0,457 
−
Z1 = 0,0297 + j 0,371344 [Ω/km]
−
 DMG 
Y1 = jω 2 πε0 ln 

RMG


−
−1
 3 8,5.8,5.17 

Y1 = jω 2 πε0 ln 
 0,014795. 0,457 
−
Y1 = j 4,30507 [µS/km]
−1
Calculando γ e Zc
−
γ=
−
γ=
− −
Z1 . Y1
(0,0297 + j 0,371344).10−3. j 4,30507.10−9
−
γ = 5,0522 .10−5 + j 0,00126539 [km-1]
α = 5,0522 10−5 Np/km
β = 1,26539 10−3 rad/km
Zc =
−
Z1
−
Y1
−
(0,0297 + j 0,371344)10−3
−
Zc =
−
j 4,30507 10−9
Zc = 293,93 - 11,7 Ω ≈ 293 Ω
Modelo π da linha
O modelo π da linha é dado por :
Ek
k
rkm + j xkm
Em
m
Ikm
j ykm
rkm + jx km = Z1' L
j ykm
senh(γL)
γL
= (0,0297 + j 0,371344)100
(
)
senh( 5,0522 .10−5 + j 0,00126539 100)
(5,0522 .10−5 + j0,00126539)100
rkm + jx km = 2,95419 + j 37,0362Ω
L tanh( γ L 2)
y km = Y1
2
γL
2
−
= j 4,30507 .50
−
(
)
tanh( 5,0522 .10−5 + j 0,00126539 50)
(5,0522 .10−5 + j0,00126539)50
y km = j 215,541µS
Modelo da carga – cálculo do
fluxo
O modelo π da linha é dado por :
Ek
k
rkm + j xkm
Em
m
Ikm
j ykm
rkm + jx km = Z1' L
j ykm
senh(γL)
γL
= (0,0297 + j 0,371344)100
(
)
senh( 5,0522 .10−5 + j 0,00126539 100)
(5,0522 .10−5 + j0,00126539)100
rkm + jx km = 2,95419 + j 37,0362Ω
L
tanh(
γ
)
L
2
y km = Y1
2 γγ L
2
−
= j 4,30507 .50
−
(
)
tanh( 5,0522 .10−5 + j 0,00126539 50)
(5,0522 .10−5 + j0,00126539)50
y km = j 215,541µS
Cálculo da corrente e tensão na
carga e no gerador
Carga:
S21 = 200∠36,87° = 160 + j150MVA
200
S21-1φ =
∠36,87° = 53,33 + j50MVA
3
Assumindo Tensão nominal na Carga:
345
V2 ft = VR =
∠0° V
3
*
 S21−1φ 
 = 334,695∠ - 36,87° A
I 21 = I R = 
V 
 2-1φ 
Cálculo da tensão e correntes no Gerador:

− 
 − 
 •   cosh γ .l0  Zc.senh γ .l0   • 



 V
Vg  



 . r 
=
• 
•
−
−




 I   1 senh γ .l  cosh γ .l    I 
 g   Zc
 0
 0   r 



 

Tensão e corrente no gerador
•
•
−4




V
0
,
9920
j
6
,
3760
.
10
1
,
4685
j
36
,
98
+
+
V
 g = 
 •r 
.

•
I  
j 4,3073.10−4
0,9920+ j 6,3760.10−4   I 
 r
 g
 •  126423,13∠ − 4,39

Vg  = 
 I•   305,81∠ − 28,88 
 g
Tensão de linha no Gerador:
•
Vg linha = 3 ⋅126423,13∠ − 4,39 V
•
Vg linha = 218,93∠ − 4,39 V
Potências e perdas na linha:
•
•
S12-1φ = V g ⋅ I12 = 35,2 + j16,03 MVA
*
Pperdas = 3 ⋅ 53,3 − 35,2 = 54,30MW
Q perdas = 3 ⋅ 33,99 = 101,97MVAr
Exercício
Considere a linha do exercício anterior
alimentando uma carga trifásica equilibrada de
200 MVA fp 0,8 atrasado. A tensão nominal
de linha é 345 kV no terminal gerador.
Freqüência do sistema: 60 Hz
•Determine a potência consumida na linha e a
tensão de linha junto a carga.