Dinâmica dos Fluidos

Dinâmica dos Fluidos
(* Preparado por C.A. Bertulani para o projeto de Ensino de Física a Distância)
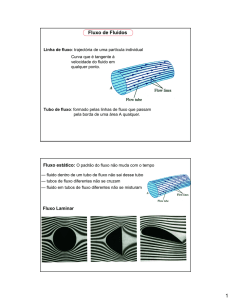
Equação de continuidade
Considere uma caixa de água conectada a pedaços de tubos com diâmetros
diversos, ao longo do caminho em que a água escoa. Suponha também que
exista uma bomba de água no circuito. Um circuito muito simples é mostrado
na figura abaixo
Fazendo a bomba de água funcionar por uns instantes irá acelerar a água e
começar o escoamento. A bomba cria um gradiente de pressão. Se
observarmos um dado volume de água em uma seção reta do tubo, a pressão no
lado 1 desse volume será diferente da pressão no lado 2. Isto leva a uma força
resultante no volume de água naquela seção, e ela irá se acelerar. Se a pressão
fosse a mesma em ambos os lados, a força resultante seria nula, e o volume de
água continuaria seu movimento com velocidade constante. Depois que a água
estiver fluindo a uma certa velocidade, a bomba tem que realizar um trabalho
muito menor. Ela sómente terá que trabalhar contra as forças de atrito.
A água em diferentes seções do circuito terá diferentes energias potenciais por
unidade de volume (por exemplo, por cm3). Ela também deve ter energias
cinéticas diferentes por unidade de volume. Nas seções mais estreitas ela deve
fluir mais rápido do que nas seções mais largas, já que a mesma quantidade de
água deve fluir através de cada seção transversal do tubo na mesma quantidade
de tempo.
Na figura abaixo mostramos o fluxo de massa (ou vazão) que passa por uma
seção transversal de um tubo. Ele é dado por m/ t, onde m é a quantidade de
massa que passa pela seção transversal A, por unidade de tempo t.
A quantidade de volume de fluido que passa pela área A é, V = A l . Mas,
como l = vt , temos que m = V = Av t.
Logo,
Mas, e se a área A muda de uma seção para a outra? A figura abaixo mostra os
novos parâmetros entram em nosso cálculo.
Temos que no ponto 1 , m1= 1 A 1 v1 t , e no no ponto 2, m2= 2 A 2 v2 t .
Não estamos criando nem destruindo massa. Logo, a massa m1 que flui para
uma região deve ser igual à massa m2 que sai da região.
Isto é, m1= m2
Ou seja, 1 A 1v1 t = 2 A 2 v2 t , ou
1 A 1v1 = 2 A 2 v2 ,[2.3]
ou
 A v = constante .
No caso em que a densidade do fluido é constante, a equação de continuidade
será dada por
A v = constante .
Equação de Bernoulli
A energia potencial da água muda enquanto ela se move. Enquanto que a água
se move, a mudança na energia potencial é a mesma que aquela de um volume
V que se movimentou da posição 1 para a posição 2. A energia potencial da
água no resto do tubo é a mesma que a energia potencial da água antes do
movimento. Logo, temos que:
mudança na energia potencial = massa da água em V  g  mudança na
altitude
= densidade  V  g  (h2 � h1) =  V g (h2 � h1).
A energia cinética da água também muda. Novamente, só precisamos achar a
mudança na energia cinética em um pequeno volume V, como se a água na
posição 1 fosse substituida pela água na posição 2 (veja a figura acima). A
energia cinética da água no resto do tubo é a mesma que a energia cinética
antes do movimento. Logo, temos que
mudança na energia potencial = ½ m v22 � ½ m v12 = ½  V v22 � ½  V v12
.
Se a força sobre a água na posição 1 é diferente do que a força da água na
posição 2, existe um trabalho sobre a água à medida que ela se move. A
quantidade de trabalho é W = F1 l1 � F2 l2. Mas, força = pressão vezes área,
de modo que W = p1 A1 l1 � p2 A2 l2 = p1 V - p2 V .
O trabalho deve ser igual à mudança na energia. Logo,
p1 V - p2 V =  V g (h2 � h1) + ½  V v22 � ½  V v12
ou
p1 V +  V g h1+ ½  V v12 = p2 V +  V g h2 + ½  V v22.
Dividindo por V, temos que
p1 +  g h1+ ½  v12 = p2 +  g h2 + ½  v22
ou
p +  g h+ ½  v2= constante.
[1.5]
Esta é a equação de Bernoulli. Ela implica que, se um fluido estiver escoando
em um estado de fluxo contínuo, então a pressão depende da velocidade do
fluido. Quanto mais rápido o fluido estiver se movimentando, tanto menor será
a pressão à mesma altura no fluido.
Aplicações da equação de Bernoulli
Aviões: A asa de um avião é mais curva na parte de cima. Isto faz com que o
ar passe mais rápido na parte de cima do que na de baixo. De acordo com a
equação de Bernoulli, a pressão do ar em cima da asa será menor do que na
parte de baixo, criando uma força de empuxo que sustenta o avião no ar.
Vaporizadores: Uma bomba de ar faz com que o ar seja empurrado
paralelamente ao extremo de um tubo que está imerso em um líquido. A
pressão nesse ponto diminui, e a diferença de pressão com o outro extremo do
tubo empurra o fluido para cima. O ar rápido também divide o fluido em
pequenas gotas, que são empurradas para frente.
Chaminé: O movimento de ar do lado de fora de uma casa ajuda a criar uma
diferença de pressão que expulsa o ar quente da lareira para cima, através da
chaminé.
Medidores de velocidade de um fluido: Na figura (a) abaixo, se existir ar em
movimento no interior do tubo, a pressão P é menor do que P0, e aparecerá
uma diferença na coluna de fluido do medidor. Conhecendo a densidade do
fluido do medidor, a diferença de pressão, P-P0 é determinada. Da equação de
Bernoulli, a velocidade do fluido dentro do tubo, v, pode ser determinada.
O medidor da figura (b) acima pode determinar a diferença de velocidade entre
dois pontos de um fluido pelo mesmo princípio.
Os medidores abaixo também são baseados no mesmo princípio. Todos esses
tipos de medidores são conhecidos como medidores de Venturi.