equação de bernoulli

ESTV | DEMad
Operações de Transferência
EQUAÇÃO DE BERNOULLI
relação fundamental da mecânica dos fluidos;
expressão que relaciona a pressão com a velocidade do fluido e a altura do tubo;
“princípio de Bernoulli” – quando a velocidade do escoamento aumenta, a pressão do fluido
diminui;
o resultado da equação é consequência da conservação da energia aplicada ao fluido;
deduz-se a partir do teorema do trabalho-energia: o trabalho realizado pela resultante das forças
que actuam num sistema é igual à variação da energia cinética do sistema:
W = ∆K + ∆U = ∆EC + ∆E P
(1)
W é o trabalho realizado sobre o sistema pelas forças de pressão
∆K, ∆EC é a variação da energia cinética
∆U, ∆EP é a variação da energia potencial
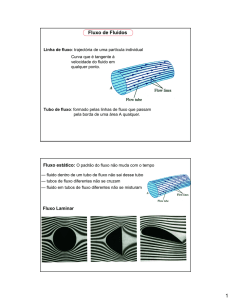
Figura 1 – Uma quantidade de fluido move-se ao longo de uma conduta, desde a posição indicada em (a)
até à posição representada em (b).
Equação Bernoulli | 1/5
ESTV | DEMad
Operações de Transferência
Figura 1 > determinar o trabalho – W – realizado pela força resultante sobre o sistema:
o W realizado sobre o sistema pela força de pressão p1A1: p1A1∆l1
o W realizado sobre o sistema pela força de pressão p2A2: -p2A2∆l2 (é negativo – o sistema
realiza um trabalho positivo)
∆V
o W= p1A1∆l1 - p2A2∆l2= (p1 - p2)∆
(2)
durante ∆t, um volume de fluido ∆V= A1∆l1 com massa ∆m=ρ
ρ∆V entra no tubo através da secção
A1, trazendo uma energia cinética
1 2 1
mv1 = ρ∆Vv12 . Analogamente, durante este intervalo, igual
2
2
massa de fluido deixa o tubo pela secção A2, levando consigo uma energia cinética
variação da enercia cinética - v∆
∆EC =
1
ρ∆V (v22 − v12 )
2
1
ρ∆Vv22 :
2
(3)
a energia potencial da massa que entra em A1, no tempo ∆t, é ∆mgy1==ρ∆Vgy1 e a energia
potencial da massa que sai em A2, é ∆mgy2=ρ∆Vgy2:
variação da energia potencial - ∆EP = ρ∆Vg(y2-y1)
(4)
Combinando as equações 2, 3 e 4 no teorema do trabalho-energia – eq. 1, obtém-se
( p1 − p2 )∆V =
1
ρ∆V (v22 − v12 ) + ρ∆Vg ( y 2 − y1 )
2
ou
( p1 − p2 ) =
1
ρ (v22 − v12 ) + ρg ( y2 − y1 )
2
ou
Equação Bernoulli | 2/5
ESTV | DEMad
p1 +
Operações de Transferência
1 2
1
ρv1 + ρgy1 = p2 + ρv22 + ρgy2
2
2
ou seja
p+
1 2
ρv + ρgy = constante
2
Equação Bernoulli para um fluido: - não viscoso; - incompressivel; - estado estacionário
p+
1 2
ρv + ρgz = constante
2
p1 +
ou
1 2
1
ρv1 + ρgz1 = p2 + ρv22 + ρgz2
2
2
(I)
a soma da pressão (p), da energia cinética por unidade de volume (
1 2
ρv ) e da energia potencial
2
por unidade de volume ( ρgz ) tem o mesmo valor em todos os pontos de uma linha de corrente;
esta forma é conveniente para o escoamento de gases, já que as variações de cota são
frequentemente sem importância, desaparecendo ( ρgz ); cada termo é dado em metro-newtons por
metro-cúbico; a lei de variação de pressão com a altura num fluido em repouso está incluída na
equação de Bernoulli como caso especial: com o fluido em repouso v1=v2=0, e então
p1 − p2 = ρg ( z2 − z1 )
LEI HIDROSTÀTICA
Se dividirmos a equação I por ρ, obtemos
p1 v12
p2 v22
+ + gz1 =
+ + gz2
ρ 2
ρ 2
(II)
em que cada parcela representa energia por unidade de massa
p
- energia de pressão / unidade de massa
ρ
v2
- energia cinética / unidade de massa
2
Equação Bernoulli | 3/5
ESTV | DEMad
Operações de Transferência
gz - energia potencial / unidade de massa
Equação Bernoulli | 4/5
ESTV | DEMad
Operações de Transferência
Se dividirmos esta equação (II) pela aceleração da gravidade obtemos:
p1 v12
p
v2
+
+ z1 = 2 + 2 + z2
ρg 2 g
ρg 2 g
(III)
em que cada parcela interpreta-se como energia por unidade de peso (metro-newtons por newton),
ou seja cada parcela representa a carga (metro):
p
- carga de pressão (m)
ρ
v2
- carga cinética (m)
2
gz - carga potencial (m)
esta forma é particulermente conveniente para tratar problemas de liquídos com superfícies livres.
Se no percurso do fluido em movimento se perder energia entre o ponto 1 e 2, há perda de carga e a
equação III escreve-se
p1 v12
p2 v22
+
+ z1 =
+
+ z2 + Perda de Carga
ρg 2 g
ρg 2 g
Equação Bernoulli | 5/5