Distribuição de z Áreas sob a curva normal padrão. Para

FACULDADE VÉRTICE UNIVÉRTIX
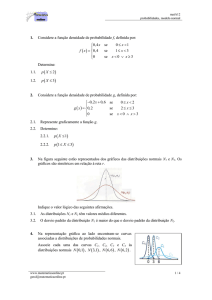
Credenciada junto ao MEC: Portaria 1.084/2007
DISCIPLINA: Estatística e Probabilidade
PROFa: Irlane Bastos Costa
TURMA: Engenharia Civil 4o período
DISTRIBUIÇÕES DE PROBABILIDADE
Setembro, 2012
1. DISTRIBUIÇÕES DE PROBABILIDADE
1.1 INTRODUÇÃO
As distribuições de frequências de amostras foram tratadas no item estatística
descritiva. Neste capítulo, são apresentadas as distribuições de probabilidade de
populações. A distribuição de frequências de uma amostra é uma estimativa da
distribuição de probabilidade da população correspondente. Se o tamanho da amostra for
grande, podemos esperar que a distribuição de frequências da amostra seja uma boa
aproximação da distribuição de probabilidade da população.
Na condução de pesquisas empíricas, bem como na busca de soluções para um
grande número de problemas práticos, estudos das características de amostras,
distribuições de frequências, gráficos, medidas de posição, dispersão etc. são de
fundamental importância. Todavia, quando pretendemos estudar, teórica e praticamente,
variáveis de uma população, as distribuições de probabilidade são mais adequadas. As
análises das distribuições de probabilidades possibilitam a construção de modelos que
nos auxiliam no entendimento de fenômenos do mundo real.
Intuitivamente pode-se definir probabilidade como:
número de casos favoráveis a A
p(A) = ---------------------------------------------número total de casos possíveis
Ao conjunto desses casos possíveis dá-se o nome de espaço amostral (S). E ao
conjunto desses casos favoráveis a A dá-se o nome de evento A.
Exemplo 1) Probabilidade de se obter um número par como resultado de um
lançamento de um dado:
S = {1,2,3,4,5,6} e A = {2,4,6}, então p = 3/6 = 1/2 = 0,5 ou 50 %
Exemplo 2) Probabilidade de se obter o número 4 como resultado do lançamento
de um dado:
S = {1,2,3,4,5,6} e A = {4}, então p = 1/6 = 0,167 ou 16,7 %
Exemplo 3) Probabilidade de se obter um número diferente de 4 no lançamento de
um dado:
S = {1,2,3,4,5,6} e A = {1,2,3,5,6}, então p = 5/6 = 0,833 ou 83,3 %
1.2 Eventos Complementares
O evento do exemplo 3 é denominado de complementar do evento do exemplo 2.
Ou seja, se p é a probabilidade de um evento ocorrer e q é a probabilidade de que ele não
ocorra, então:
p + q = 1 => q = 1 - p
1.3 Eventos Independentes
Dois eventos são independentes quando a realização de um não afeta a
probabilidade da realização do outro. Portanto a probabilidade de que dois eventos
independentes se realizem simultaneamente é definido por:
p = pA x pB
Também conhecida como regra do "e"
Exemplo 1) No lançamento de dois dados, simultaneamente, qual a Probabilidade
de se obter o número 1 e o número 5?
p = p1 x p5 = 1/6 x 1/6 = 1/36 = 0,028 = 2,8%
Exemplo 2) No lançamento de dois dados, simultaneamente, qual a Probabilidade
de se obter um número par e um número impar?
p = ppar x pimpar = 3/6 x 3/6 = 9/36 = 0,25 = 25%
1.4 Eventos Mutuamente Exclusivos
Dois eventos são mutuamente exclusivos quando a realização de um exclui a
realização do outro. Nesse caso a probabilidade de que um ou o outro se realize é:
p = pA + pB
Também conhecida como regra do "ou"
Deve-se observar que se tivermos A ∩ B = ∅, então p(A ∪ B) = p(A) + P(B). Mas,
se A ∩ B ≠ ∅, então p(A ∪ B) = p(A) + P(B) – p(A∩B)
Exemplo 1) A probabilidade de se obter 1 ou 5 em um lançamento de dado é:
P = p1 + p5 = 1/6 + 1/6 = 2/6 = 1/3 = 0,333 = 33,3%
Exercícios Propostos
1) Determine a probabilidade de cada evento:
a) Uma carta de ouros aparecer ao se extrair uma carta de um baralho de 52 cartas
Resp: a) p = 1/4
2) Em um lote de 12 peças, 4 são defeituosas. Sendo retiradas aleatoriamente 2
peças, calcule:
a) a probabilidade de ambas serem defeituosas;
b) a probabilidade de ambas não serem defeituosas;
c) a probabilidade de ao menos uma ser defeituosa.
Resp: a) p = 12/132 b) p = 56/132 c) p = 76/132
3) Um casal planeja ter 3 filhos. Determine a probabilidade de nascerem:
a) três homens;
b) dois homens e uma mulher.
Resp: a) p = 1/8 b) p = 3/8
4) Um baralho de 52 cartas é subdividido em 4 naipes: copas, espadas, ouros e
paus:
a) Retirando-se uma carta ao acaso, qual a probabilidade de que ela seja de ouros
ou de copas?
b) Retirando-se duas cartas ao acaso com reposição da primeira carta, qual a
probabilidade de ser a primeira de ouros e a segunda de copas?
c) Recalcular a probabilidade anterior se não houver reposição da primeira carta.
Resp: a) p = 26/52 b) p = 169/2704 c) p = 169/2652
5) Uma urna contém 20 bolas numeradas de 1 a 20. Seja o experimento: retirada
de uma bola. Calcular as probabilidades dos eventos:
A ) A= {retirar um múltiplo de 2};
B) A = {retirar um múltiplo de 5};
C) A = {retirar o número 1};
D) A = {retirar um número ímpar}
6) Considerando a urna do exercício anterior e o experimento retirar duas bolas,
sem reposição da primeira. Calcular as probabilidades dos eventos:
A) A = {retirar o numero 1 e o numero 2};
B) A = {retirar apenas números pares};
C) A = {retirar apenas números impares};
2. DISTRIBUIÇÕES DE PROBABILIDADES DE VARIÁVEIS ALEATÓRIAS DISCRETAS
Relembrando:
Variável é o conjunto de resultados possíveis de um fenômeno. A variável pode ser
qualitativa, quando seus valores são expressos por atributos (ex: sexo, cor), ou pode ser
quantitativa, quando seus valores são expressos em números.
A variável quantitativa pode ser contínua, quando assume qualquer valor entre dois
limites (ex: peso, altura, medições), ou pode ser discreta, quando só pode assumir valores
pertencentes a um conjunto enumerável (ex: número de filhos, contagens em geral).
Seja a seguinte distribuição de frequência:
Número de Acidentes Frequências
Por dia em 1 mês
0
22
1
5
2
2
3
1
Total
30
Através dos dados apresentados pode-se calcular a probabilidade de em um dia:
não ocorrer nenhum acidente: P = 22/30 = 0,73
ocorrer 1 acidente: P = 5/30 = 0,17
ocorrer 2 acidentes: P = 2/30 = 0,07
ocorrer 3 acidentes: P = 1/30 = 0,03
Podemos então elaborar uma tabela denominada distribuição de probabilidade:
Número de Acidentes
Por dia em 1 mês
0
1
2
3
Total
Probabilidade
0,73
0,17
0,07
0,03
1,00
EXEMPLO 1: Vamos encontrar a distribuição de probabilidade da variável número de
caras encontradas no lançamento de três moedas.
Logo, o espaço amostral (S) é formado pelas possíveis combinações das faces das
três moedas lançadas simultaneamente
S = {ccc, cck, ckk, ckc, kck, kcc, kkc, kkk};
E a variável aleatória discreta é X = número de caras
x = O - kkk
x = 1 – kkc, kck, ckk
x = 2 - cck, ckc, kcc
x = 3- ccc
Eis a distribuição de probabilidade expressa por uma tabela:
xi
0
1
2
3
P(xi) 1/8 3/8 3/8 1/8
2.1 DISTRIBUIÇÃO BINOMIAL
Trata-se de um modelo que dá a probabilidade do número de sucessos quando são
realizadas n provas do mesmo tipo - o experimento é repetido n vezes. Cada experimento
admite dois resultados - sucesso ou fracasso - com probabilidade p de sucesso e 1 - P =
de fracasso, constantes em cada uma das provas. São muitas as variáveis aleatórias
discretas que possuem tais características. A mais familiar, provavelmente, é o
lançamento de uma moeda n vezes, por exemplo: n = 20. Cada prova, ou experimento,
admite apenas dois resultados: cara ou coroa. Sem prejuízo para o cálculo, pode-se
admitir que sucesso, por exemplo, é dar coroa, enquanto o fracasso é verificado quando o
resultado for cara. Se a moeda é honesta, as probabilidades p = ½ de sucesso e q = 1 –
½ de fracasso são constantes em cada um dos lançamentos. O modelo de distribuição
de probabilidade binomial possibilitará o cálculo das probabilidades da variável Y: número
de sucessos. Y poderá ser 0 (Nenhuma coroa aparece quando se joga a moeda 20
vezes), 1 (uma coroa aparece), 2, 3, ... , 20.
Veja outros exemplos
• Respostas de um teste com diversas questões do tipo F ou V
• Escolher entre um produto bom ou defeituoso
• Sexo das crianças nascidas em determinada maternidade
• Atirar em um alvo , atingindo-o ou não
• Fumantes ou não fumantes em um grupo de adultos
• Alunos de uma escola vacinados ou não vacinados
Experimentos com resultados múltiplos podem ser tratados como binomiais,
quando se consideram apenas dois resultados. Por exemplo: jogar um dado e verificar o
resultado da face que se apoia na superfície não é uma prova binomial, porem se
considerarmos sucesso sair o 6, e fracasso outro resultado diferente de 6, teremos um
experimento adequado ao modelo binomial.
Para utilizarmos a distribuição binomial, as seguintes hipóteses devem ser
atendidas:
• São realizadas n provas do mesmo tipo (idênticas).
• Cada prova admite dois resultados possíveis, um chamado sucesso e o outro
fracasso.
• As probabilidades p, de sucesso, e 1 - P = q, de fracasso, permanecem
constantes em todas as provas.
• Os resultados das provas são independentes, ou seja, o resultado de uma não
afeta o resultado da outra.
A fórmula do cálculo da probabilidade de certo número y de sucessos em n provas
é dada por:
n
P(Y  y )  p y q n y  
 y
onde:
n = número de provas ou repetições do experimento
y = número de sucessos
n - y = número de fracassos
p = a probabilidade de sucesso em cada prova
q = 1 - P é a probabilidade de fracasso em cada prova
n
  = o número de combinações de n elementos, tomados y a y.
 y
n
n!
  
 y  n!n  y !
Exemplo 1) Uma moeda é lançada 5 vezes seguidas e independentes. Calcule a
probabilidade de serem obtidas 3 caras nessa prova.
n=5
y=3
p = 1/2
q = 1-p = 1-1/2 = ½
n  1   1 
5! 1 1
5
        
   20 
8
 y   2   2  3!2! 8 4
3
P(Y  y)  p q
y
n y
2
Exemplo 2) Dois times de futebol, A e B, jogam entre si 6 vezes. Encontre a
probabilidade do time A ganhar 4 jogos. (p = 1/3)
n=6
y=4
p = 1/2
q = 1-p = 1-1/2 = 1/2
n  1   1 
6!
1 1
15
        
  15 
64
 y   2   2  4!2! 16 4
4
P(Y  y)  p q
y
n y
2
Exemplo 3) Admite-se que uma válvula eletrônica, instalada em determinado circuito,
tenha probabilidade 0,3 de funcionar mais de 600 horas. Se ensaiarmos 10 válvulas, qual
será a probabilidade de que:
A) Nenhuma funcione mais de 600 h?
B) Todas funcionem mais de 600h?
C) Apenas uma funcione mais de 600h?
Temos:
Y = variável aleatória: número de sucessos nos 10 ensaios. Assim, y = O, 1,2, ...,
10.
P = 0,3 probabilidade de sucesso de cada válvula (funcionar mais de 600 h)
q = 1 - 0,3 = 0,7 probabilidade de fracasso de cada válvula (funcionar menos de
600 h)
n = 10 ensaios
Então:
p(Y  y )  0,3  0,7 
10  y
y
10 
  
 y
Logo:
10 
    0,0282
0
10 
1
101
B) p(Y  1)  0,3  0,7      0,1211
1
10
1010 10 
    0,000056
C) p(Y  10)  0,3  0,7 
10 
A) p(Y  0)  0,3  0,7 
0
10 0
MEDIDAS DE POSIÇAO E DISPERSAO
Média:
 y  E y   np
Variância:
 y2  var y  npq
Desvio Padrão:
 y   y2  npq
Moda: O valor mais provável da moda de uma distribuição binomial é o numero
inteiro compreendido entre np + p e n. A moda toma um valor próximo da media np.
Observações importantes
1. Uma distribuição binomial fica caracterizada pelos parâmetros n e p.
2. Se n for pequeno, os cálculos serão relativamente fáceis. Contudo, se n for
relativamente grande, os cálculos tornam-se cansativos. Felizmente, dispomos de
calculadoras, tabelas apropriadas.
3. Para qualquer n, a distribuição binomial será simétrica, se p = q = 0,5; será
assimétrica à direita, se p > q, e assimétrica à esquerda, se p < q.
EXERCÍCIOS PROPOSTOS
1) Uma moeda é jogada 10 vezes. Calcule as seguintes probabilidades:
a) de ocorrer seis caras;
b) de dar pelo menos 8 caras;
c) de não ocorrer nenhuma coroa;
2) Admitindo que os nascimentos de meninos e meninas sejam iguais, calcular a
probabilidade de um casal com seis filhos ter quatro filhos homens e duas mulheres.
3) Se 5% das lâmpadas de certa marca são defeituosas, ache a probabilidade de que,
numa amostra de 100 lâmpadas, escolhidas ao acaso, tenhamos:
a) nenhuma defeituosa
b) três defeituosas
4) Jogando-se um dado três vezes, determine a probabilidade de se obter um múltiplo de
3 duas vezes.
Resp: p = 2/9
5) Seis parafusos são escolhidos ao acaso da produção de uma certa máquina, que
apresenta 10% de peças defeituosas. Qual a probabilidade de serem defeituosos dois
deles ?
Resp: p = 0,0984
6) Dos estudantes de um colégio, 41 % fumam cigarro. Escolhem-se seis ao acaso para
darem uma opinião sobre o fumo. Determine a probabilidade de:
a) nenhum dos seis ser fumante
b) todos os seis fumarem
c) ao menos a metade dos seis ser fumante
Resp: a) p = 4,22% b) p = 0,48% c) 47,65%
7) 12% dos que reservam lugar num vôo faltam ao embarque. O avião comporta 15
passageiros.
a) Determine a probabilidade de que todos os 15 que reservaram lugar compareçam ao
embarque.
b) Se houve 16 pedidos de reserva, determine a probabilidade de uma pessoa ficar de
fora.
Resp: a) p = 14,70% b) p = 12,93%
2.2 DISTRIBUIÇÃO DE POISSON
A distribuição de Poisson representa um modelo probabilístico adequado para o
estudo de um grande número de fenômenos observáveis. Eis alguns exemplos:
• Chamadas telefônicas por unidade de tempo.
• Defeitos por unidade de área.
• Acidentes por unidade de tempo.
• Chegada de clientes a um supermercado por unidade de tempo.
• Número de glóbulos sanguíneos visíveis ao microscópio por unidade dê área.
• Número de partículas emitidas por uma fonte de material radioativo por unidade
de tempo.
Seja X uma variável aleatória igual ao número de ocorrências (sucessos).
Quando se realizam (ou se observam) resultados de fenômenos semelhantes aos
dos exemplos anteriores, X poderá assumir os valores: O, 1, 2, ...
Ao aplicar o modelo de Poisson, o interesse poderá ser, por exemplo, calcular a
probabilidade de receber cinco chamadas telefônicas, em três minutos, em dado
aparelho: P(X = 5chamadas/3 min).
De início, poderíamos pensar no uso do modelo binomial, porém não sabemos qual
o número de provas (n = ?), nem a quantidade de fracassos: quantos chamadas não
ocorreram?
Se adotamos algumas hipóteses quanto à taxa de freqüência (λ) dessas
ocorrências por uma pequena unidade de tempo: (Δt), ou, conforme o caso: (Δs) =
unidade de área ... , e algumas outras premissas, enunciadas a seguir, obtemos o modelo
de Poisson como limite da distribuição binomial, quando n tende ao infinito.
Hipóteses do modelo de Poisson
H1 - A probabilidade de uma ocorrência em um intervalo Δt (ou Δs, ou ... ) é
constante e proporcional ao tamanho do intervalo. Isto é: P(X = 1, Δt) = λΔt.
H2 - A probabilidade de mais de uma ocorrência em um intervalo Δt (ou Δs, ou ... )
é igual a zero. Isto é: P(X > 1, Δt) = O.
H3 - O número de ocorrências constitui variáveis aleatórias independentes.
A expressão que dá a probabilidade de x sucessos em um intervalo t (tempo, área
... ) é:
(t ) x .e  t
p ( X  x, t ) 
x!
onde:
λ = coeficiente de proporcionalidade, ou taxa de frequência por unidade de tempo,
área,
t = tempo, área,
e = base dos logaritmos naturais (2,71828)
x = número de ocorrências (sucessos)
Considerando que a média da distribuição é dada por λt, ou seja, μ = λt, temos:
p( X  x / t ) 
 x .e  
x!
A variância da distribuição também é dada por λt, ou seja:
 2  t .
A moda corresponde ao maior inteiro contido em λt. Se λt for inteiro, então haverá
duas modas nos pontos: x = λt e x – 1 = λt – 1.
Os valores de e   são encontrados em tabelas próprias.
EXEMPLO 4: Experiências passadas indicam que, em média, há duas chamadas
por hora em certo telefone. Vamos calcular as probabilidades de, em uma hora, o telefone
receber: nenhuma chamada; uma; duas; três; ...
Solução: sabe-se que μ = λt, logo 2 = λ1 :. λ = 2, ou ainda μ = 2.
Nenhuma chamada
Uma chamada
p( X  0 / 1h) 
 x .e  
x!
2 0.e 2

 0,1353
0!
21.e 2
p( X  1 / 1h) 
 0,2706
1!
Duas chamadas
Três chamadas
2 2.e 2
p( X  2 / 1h) 
 0,2706
2!
2 3.e 2
p( X  3 / 1h) 
 0,1804
3!
.
.
.
Nove chamadas
2 9.e 2
p( X  9 / 1t ) 
 0,0002
9!
A tabela de distribuição de probabilidade da variável X, número de chamadas
telefônicas, será:
xi
P(xi)
0
1
2
3
4
0,1353 0,2706 0,2706 0,1804 0,0902
Observe:
5
6
7
0,0361 0,0120 0,0034
8
9
0,0009 0,0002
 p( x )  0,9997  1 Esse resultado é explicado, pois x, número de
i
sucesssos, teoricamente, tende ao infinito. Nesse caso, o infinito foi x = 9.
Quanto às medidas de posição:
Média: λt = 2, inteiro, temos duas modas: M01 = 2 e M02 = 1
Quanto às medidas de dispersão:
Variância:
 2  t  2
Desvio padrão:
  t  2  1,4142
Coeficiente de variação:
C.V . 
1,4142
 100  70,71%
2
EXERCÍCIO DE FIXAÇÃO: O pessoal de inspeção de qualidade afirma que os
rolos de fita isolante apresentam, em média, uma emenda a cada 50 metros. Admitindo
que a distribuição do número de emendas é dada pela Poisson, vamos callcular as
probabilidades:
a) de nenhuma emenda em um rolo de 125 metros:
b) de ocorrerem no máximo duas emendas em um rolo de 125 metros
c) de ocorrer pelo menos urna emenda em um rolo de 100 metros
EXERCÍCIOS PROPOSTOS
1. Admitindo que X tem distribuição de probabilidade de Poisson, encontrar as
probabilidades:
a) P(X = 5) quando μ = 3,0;
b) P(X ≤ 2) quando μ = 5,5;
c) P(X ≥ 4) quando μ = 7,5;
d) P(X = 8) quando μ = 4,0.
2. Uma amostra aleatória de 230 pessoas é selecionada. Cada indivíduo da
amostra responde se prefere comprar um PC ou um VCR. Assumindo que 3%
do público prefere um PC, determinar, aproximadamente, a probabilidade de um
grupo de 10 pessoas preferir PC.
3. Uma fábrica de pneus verificou que, ao testar seus pneus nas pistas, havia em
média um estouro de pneu a cada 5.000 km.
a) Qual a probabilidade de que num teste de 3.000 km haja no máximo um pneu
estourado?
b) Qual a probabilidade de que um carro ande 8.000 km sem estourar nenhum
pneu?
4. Certo posto de bombeiros recebe em média três chamadas por dia. Calcular a
probabilidade de:
a) receber quatro chamadas num dia;
b) receber três ou mais chamadas num dia.
5. A média de chamadas telefônicas numa hora é três. Qual a probabilidade de:
a) receber exatamente três chamadas numa hora?
b) receber quatro ou mais chamadas em 90 minutos?
6. Na pintura de paredes, aparecem defeitos em média na proporção de um
defeito por metro quadrado. Qual a probabilidade de aparecerem três defeitos
numa parede de 2 x 2 cm?
7. Uma loja atende em média a dois clientes por hora. Calcular a probabilidade de
em uma hora:
a) atender exatamente a dois clientes;
b) atender a três clientes.
8. Suponha 400 erros de impressão distribuídos aleatoriamente em um livro de
500 páginas. Encontre a probabilidade de que dada página contenha:
a) nenhum erro;
b) exatamente dois erros.
3. DISTRIBUIÇÃO DE PROBABILIDADE DE VARIÁVEIS CONTÍNUAS
Entre as distribuições teóricas de variável contínua, a mais empregada é a
distribuição normal.
A equação da curva é a seguinte:
f ( x) 
1
2
e 0,5 x    /  
2
Esta é A função de densidade da probabilidade da distribuição normal.
Se uma variável aleatória x tem distribuição normal com média  e variância  2 ,
diz-se que x ~ N(  ,  2 )
Analise Gráfica
A figura a seguir mostra uma curva normal típica, com seus parâmetros descritos
graficamente. A média é o centro da curva. A distribuição de valores maiores que a média
e a dos valores menores que a média é perfeitamente simétrica, ou seja, se passarmos
uma linha exatamente pelo centro da curva teremos duas metades, sendo que cada uma
delas é a imagem especular da outra.
As extremidades da curva se estendem de forma indefinida ao longo de sua base
(o eixo das abcissas) sem jamais tocá-la. Portanto, o campo de variação da distribuição
normal se estende de - infinito a + infinito.
Assim sendo, a curva apresenta uma área central em torno da média, onde se
localizam os pontos de maior frequência e também possui áreas menores,
progressivamente mais próximas de ambas as extremidades, em que são encontrados
valores muito baixos de x (à esquerda) ou escores muito altos (à direita), ambos
presentes em baixas frequências.
Como em qualquer função de densidade de probabilidade a área sob a curva
normal é 1, sendo a frequência total igual a 100%. Assim, a curva normal é uma
distribuição que possibilita determinar probabilidades associadas a todos os pontos da
linha de base.
Portanto, tomando-se quaisquer dois valores pode-se determinar a proporção de
área sob a curva entre esses valores. E essa área é a própria frequência da característica
que ela determina.
É muito importante entender como a curva é afetada pelos valores da média e do
desvio padrão.
Note-se que, se diferentes amostras apresentarem o mesmo valor de média e
diferentes valores de desvios padrão, a distribuição que tiver o maior desvio padrão se
apresentará mais achatada (c), com maior dispersão em torno da média. Aquela que tiver
o menor desvio padrão (a) apresentará o maior valor de frequência e acentuada
concentração de indivíduos em valores próximos à média (a).
Já, distribuições normais com valores de médias diferentes e o mesmo valor de
desvio padrão possuem a mesma dispersão, mas diferem quanto à localização no eixo
dos X.
PADRONIZANDO A DISTRIBUIÇÃO NORMAL
Todas as curvas normais representativas de distribuições de frequências podem
ser transformadas em uma curva normal padrão. A Distribuição Normal Padrão é
caracterizada por ter média (  ) igual a zero e desvio padrão (  2 ) igual a 1.
Utilizando a formula de transformação, qualquer variável aleatória normal X é
convertida em uma variável normal padronizada Z.
Z
X 

onde:
σ e o desvio padrão
μ e a media aritmética
A figura mostra que o desvio-padrão controla o grau para o qual a distribuição se
"espalha" para ambos os lados da curva. Percebe-se que aproximadamente toda a
probabilidade está dentro de ± 3σ a partir da média.
A equação da curva de z é:
Assim, a variável x cuja distribuição é N(  ,  2 ) é transformada na forma padronizada z
cuja distribuição é N(0,1). Essa é a distribuição normal padrão, que já está tabelada, pois
os parâmetros da população (desvio padrão e média) são conhecidos.
Então, se forem tomados dois valores específicos, pode-se determinar a proporção
de área sob a curva entre esses dois valores.
Para a distribuição Normal, a proporção de valores caindo dentro de um, dois, ou
três desvios padrão da média são:.
entre
é igual a
 ± 1
68,26% (1)
 ± 2
95,44% (2)
 ± 3
99,74% (3)
Z - DADOS TABELADOS
Como se chegou a esses valores?
Para responder essa pergunta é necessário conhecer a distribuição de z, que já
está tabelada. Note-se que a Tabela de z determina a área a partir do número de desviospadrão, os quais são lidos assim:
O valor de z será encontrado na intersecção entre a coluna e a linha, sendo
adimensional.
Verificando a tabela, percebe-se que para os valores negativos de z as áreas são
obtidas por simetria, ou seja, existe o mesmo conjunto de valores, com sinal negativo,
para o lado esquerdo da média, pois a tabela é especular.
Os valores de z permitem delimitar a área sob a curva, pois, como no eixo Y do
gráfico está a frequência da variável, a área sob a curva tem o mesmo valor da
probabilidade de ocorrência daquela característica.
Exemplo 1: Qual é a área sob a curva normal contida entre z = 0 e z = 1?
Procura-se o valor 1 na primeira coluna da tabela e o valor da coluna 0,00. O valor
da intersecção é de 0,3413, ou seja 34,13%.
Entretanto, lembrando que a curva normal é simétrica, sabe-se que a área sob a
curva normal contida entre z = 0 e z = -1 também é 34,13%. Portanto, a área referente a
-1 < z < 1 vale a soma de ambas, ou seja, 68,26%.
Recordando que o valor central corresponde a média, pode-se traçar o seguinte
gráfico, em que se percebe que, excetuando-se os valores centrais, sobram apenas
15,87% para cada lado da curva.
Exemplo 2: Assim sendo, considerando a área sob a curva normal, qual é a área
correspondente a exatos 95% da curva?
z = 95% = 0, 95
0, 95 / 2 = 0,4750
Procurando esse valor (0,4750) na tabela de z chega-se a 1,96.
Portanto, como o valor da área é o mesmo valor da probabilidade, se uma variável
x tem distribuição normal, com média  e desvio padrão σ, a probabilidade de se sortear
da população de valores de x um valor contido no intervalo  ± 1,96σ é igual a 95%
(47,5% para cada lado da curva ) e a probabilidade de se sortear da população de valores
de x um valor não contido no intervalo  ± 1,96σ é igual a 5% ( 2,5% em cada extremo da
curva ).
EXERCÍCIOS PROPOSTOS
o
1) Seja um teste de inteligência aplicado a um grupo de 50 adolescentes do 3 ano
colegial. Obteve-se uma distribuição normal com média 50 e desvio padrão 6. Perguntase qual a proporção de alunos com notas superiores a 60?
2) Com os dados do problema anterior, averiguar o número de alunos com notas
entre 35 e 45.
3) Com os dados do problema anterior, qual é a nota abaixo da qual estão 75% dos
alunos ?
4) Achar a probabilidade de um valor escolhido ao acaso seja superior a 50 em
uma distribuição normal de média 35 e desvio padrão 8.
Resp: 0,0304 ou 3,04 %
5) Seja a distribuição normal de média 6,74 e desvio padrão de 2,3. Qual a
probabilidade de encontrar um valor inferior a 3,4 ?
Resp: 0,0735 ou 7,35 %
6) Um teste padronizado de escolaridade tem distribuição normal com média 100 e
desvio padrão 25. Determine a probabilidade de um indivíduo submetido ao teste ter nota:
a) maior que 120
b) entre 75 e 125
c) entre 115 e 125
d) qual é a nota abaixo da qual estão 70% dos alunos
Resp: a) p = 21,19 % b) p = 68,26% c) p = 11,55% d) 113
7) Os salários dos funcionários de uma escola têm distribuição normal com média
de R$ 1500,00, e desvio padrão de R$ 200,00. Qual a proporção de funcionários que
ganham:
a) entre R$ 1400 e R$ 1600 ?
b) acima de R$ 1500 ?
c) acima de R$ 1400 ?
d) abaixo de R$ 1400 ?
e) acima de R$ 1650 ?
Resp: a) p = 38,3 % b) p = 50% c) p = 69,15% d) p = 30,85% e) p = 22,66%
Distribuição de z
Áreas sob a curva normal padrão. Para os valores negativos de z são obtidas por simetria.
z
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,0 0,0000 0,0040 0,0080 0,0120 0,0160 0,0199 0,0239 0,0279 0,0319 0,0359
0,1 0,0398 0,0438 0,0478 0,0517 0,0557 0,0596 0,0636 0,0675 0,0714 0,0753
0,2 0,0793 0,0832 0,0871 0,0910 0,0948 0,0987 0,1026 0,1064 0,1103 0,1141
0,3 0,1179 0,1217 0,1255 0,1293 0,1331 0,1368 0,1406 0,1443 0,1480 0,1517
0,4 0,1554 0,1591 0,1628 0,1664 0,1700 0,1736 0,1772 0,1808 0,1844 0,1879
0,5 0,1915 0,1950 0,1985 0,2019 0,2054 0,2088 0,2123 0,2157 0,2190 0,2224
0,6 0,2257 0,2291 0,2324 0,2357 0,2389 0,2422 0,2454 0,2486 0,2517 0,2549
0,7 0,2580 0,2611 0,2642 0,2673 0,2703 0,2734 0,2764 0,2794 0,2823 0,2852
0,8 0,2881 0,2910 0,2939 0,2967 0,2995 0,3023 0,3051 0,3078 0,3106 0,3133
0,9 0,3159 0,3186 0,3212 0,3238 0,3264 0,3289 0,3315 0,3340 0,3365 0,3389
1,0 0,3413 0,3438 0,3461 0,3485 0,3508 0,3531 0,3554 0,3577 0,3599 0,3621
1,1 0,3643 0,3665 0,3686 0,3708 0,3729 0,3749 0,3770 0,3790 0,3810 0,3830
1,2 0,3849 0,3869 0,3888 0,3907 0,3925 0,3944 0,3962 0,3980 0,3997 0,4015
1,3 0,4032 0,4049 0,4066 0,4082 0,4099 0,4115 0,4131 0,4147 0,4162 0,4177
1,4 0,4192 0,4207 0,4222 0,4236 0,4251 0,4265 0,4279 0,4292 0,4306 0,4319
1,5 0,4332 0,4345 0,4357 0,4370 0,4382 0,4394 0,4406 0,4418 0,4429 0,4441
1,6 0,4452 0,4463 0,4474 0,4484 0,4495 0,4505 0,4515 0,4525 0,4535 0,4545
1,7 0,4554 0,4564 0,4573 0,4582 0,4591 0,4599 0,4608 0,4616 0,4625 0,4633
1,8 0,4641 0,4649 0,4656 0,4664 0,4671 0,4678 0,4686 0,4693 0,4699 0,4706
1,9 0,4713 0,4719 0,4726 0,4732 0,4738 0,4744 0,4750 0,4756 0,4761 0,4767
2,0 0,4772 0,4778 0,4783 0,4788 0,4793 0,4798 0,4803 0,4808 0,4812 0,4817
2,1 0,4821 0,4826 0,4830 0,4834 0,4838 0,4842 0,4846 0,4850 0,4854 0,4857
2,2 0,4861 0,4864 0,4868 0,4871 0,4875 0,4878 0,4881 0,4884 0,4887 0,4890
2,3 0,4893 0,4896 0,4898 0,4901 0,4904 0,4906 0,4909 0,4911 0,4913 0,4916
2,4 0,4918 0,4920 0,4922 0,4925 0,4927 0,4929 0,4931 0,4932 0,4934 0,4936
2,5 0,4938 0,4940 0,4941 0,4943 0,4945 0,4946 0,4948 0,4949 0,4951 0,4952
2,6 0,4953 0,4955 0,4956 0,4957 0,4959 0,4960 0,4961 0,4962 0,4963 0,4964
2,7 0,4965 0,4965 0,4967 0,4968 0,4969 0,4970 0,4971 0,4972 0,4973 0,4974
2,8 0,4974 0,4975 0,4976 0,4977 0,4977 0,4978 0,4979 0,4979 0,4980 0,4981
2,9 0,4981 0,4982 0,4982 0,4983 0,4983 0,4984 0,4985 0,4985 0,4986 0,4986
3,0 0,4987 0,4987 0,4987 0,4988 0,4988 0,4989 0,4989 0,4989 0,4990 0,4990
3,1 0,4990 0,4991 0,4991 0,4991 0,4992 0,4992 0,4992 0,4992 0,4993 0,4993
3,2 0,4993 0,4993 0,4994 0,4994 0,4994 0,4994 0,4994 0,4995 0,4995 0,4995
3,3 0,4995 0,4995 0,4995 0,4996 0,4996 0,4996 0,4996 0,4996 0,4996 0,4997
3,49 0,4997 0,4997 0,4997 0,4997 0,4997 0,4997 0,4997 0,4997 0,4997 0,4998
3,6 0,4998 0,4998 0,4999 0,4999 0,4999 0,4999 0,4999 0,4999 0,4999 0,4999
3,9 0,500