Oscilação () Tamanho do arquivo

Halliday
Fundamentos de Física
Volume 2
www.grupogen.com.br
http://gen-io.grupogen.com.br
O GEN | Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica,
LTC, Forense, Método, E.P.U. e Forense Universitária
O GEN-IO | GEN – Informação Online é o repositório de material suplementar dos livros dessas editoras
www.grupogen.com.br
http://gen-io.grupogen.com.br
Capítulo 15
Oscilações
15.1 Movimento oscilatório
Movimento oscilatório é um movimento periódico no
tempo, ou seja, um movimento que se repete a
intervalos regulares.
Exemplos:
• Uma linha de transmissão começa a oscilar quando
é fustigada pelo vento.
• As oscilações causadas por terremotos podem fazer
edifícios balançarem.
Às vezes as oscilações são tão fortes que provocam o
colapso de sistemas.
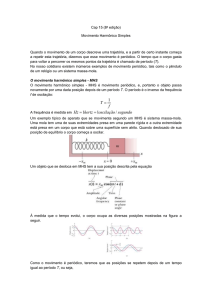
15.2 Movimento Harmônico Simples
A figura mostra uma sequência de
instantâneos de um sistema oscilatório
simples. Uma partícula se move
repetidamente para um lado e para outro
em relação ao ponto x = 0.
O tempo necessário para completar uma
oscilação é o período T. Em um intervalo
de tempo T, o sistema passa de x = +xm
para x = –xm e volta à posição inicial
x = xm.
O comprimento da seta do vetor
velocidade é proporcional à velocidade
escalar do sistema em cada ponto da
oscilação. Em x = ±xm, a velocidade é
zero.
15.2 Movimento Harmônico Simples
A frequência de uma oscilação é o número de oscilações por
segundo.
O símbolo de frequência é f e a unidade de frequência do SI é o
hertz (Hz).
A frequência está relacionada ao período através da equação
1
T=
f
15.2 Movimento Harmônico Simples
Todo movimento que se repete a intervalos regulares é
chamado de movimento periódico ou movimento harmônico.
Se o movimento é uma função senoidal do tempo, é chamado
de movimento harmônico simples (MHS).
O MHS pode ser descrito pela função
x (t ) = x m cos(ωt + φ )
onde
• xm é a amplitude (deslocamento máximo do sistema)
• t é o tempo
• ω é a frequência angular
• φ é a constante de fase ou ângulo de fase
15.2 Movimento Harmônico Simples
A figura (a) mostra o deslocamento de
dois sistemas em MHS com amplitudes
diferentes e períodos iguais.
A figura (b) mostra o deslocamento de
dois sistemas em MHS com amplitudes
iguais e períodos diferentes.
O valor da constante de fase φ depende
dos valores do deslocamento e da
velocidade do sistema no instante t = 0.
A figura (c) mostra o deslocamento de
dois sistemas em MHS com amplitudes e
períodos iguais e fases diferentes.
15.2 Movimento Harmônico Simples
No caso de um movimento oscilatório de período T,
x (t ) = x (t + T )
Como a função cosseno se repete quando o argumento
aumenta de 2π,
ω (t + T ) = ωt + 2π
→ ωT = 2π
2π
→ω =
= 2πf
T
no qualω é a frequência angular, cuja unidade no SI é o
radiano por segundo (rad/s).
15.2 Movimento Harmônico Simples
A velocidade do MHS é dada por
O valor máximo (amplitude) da velocidade é
ωxm. A velocidade está defasada de π/2 em
relação ao deslocamento.
A aceleração do MHS é dada por
A amplitude da aceleração é ω2xm.
A aceleração é proporcional ao deslocamento, mas tem o sinal
oposto.
15.3 A Lei do MHS
De acordo com a 2a lei de Newton,
F = ma = −(mω ) x = −kx
2
O MHS é o movimento executado por um sistema
submetido a uma força proporcional ao deslocamento
do sistema, com o sinal oposto ao do deslocamento.
15.3 A Lei do MHS
O sistema bloco-mola mostrado
na figura constitui um oscilador
linear que descreve um MHS.
A constante elástica da mola, k,
está relacionada à frequência
angular ω e ao período T do
oscilador por meio das equações
Exemplo: Lei do MHS
Exemplo: Lei do MHS (continuação)
Exemplo: Lei do MHS (continuação)
Exemplo: Lei do MHS (continuação)
Exemplo: Lei do MHS (continuação)
Exemplo: Lei do MHS (continuação)
15.4: A Energia do MHS
A energia potencial de um oscilador
linear está associada à mola.
A energia cinética de um oscilador
linear está associada à velocidade
do bloco.
A energia total é a soma das duas
energias.
Exemplo: Amortecedores de massa
Exemplo: Amortecedores de massa (continuação)
15.4: Um Oscilador Harmônico Angular
A figura mostra um exemplo de oscilador
harmônico angular, o chamado pêndulo de
torção, formado por um disco que gira em
um plano horizontal sustentado por um fio.
O torque associado a um deslocamento
angularθ é dado por
τ = −κθ
na qual κ é a constante de torção, que
depende do comprimento, diâmetro
e material do fio.
O período T das oscilações é dado por
T = 2π
I
κ
, na qual I é o momento de inércia do
disco.
Exemplo: Oscilador angular
15.6: Pêndulos
Em um pêndulo simples, uma partícula
de massa m está suspensa por uma das
extremidades de um fio de comprimento
L, cuja outra extremidade está fixa.
O torque associado a um deslocamento
angular θ é dado por
τ = − L( Fg sen θ ) = Iα
em que α é a aceleração angular da
partícula. Assim,
mgL
α =−
I
θ
L
T = 2π
g
Essas equações valem apenas para pequenos deslocamentos.
15.6: Pêndulos
Um pêndulo físico pode ter uma
distribuição complicada de massa. Se o
centro de massa C está a uma distância h
do ponto fixo, como na figura, temos, para
pequenas amplitudes de oscilação, um
movimento harmônico simples.
O período T das oscilações é dado por
I
T = 2π
mgh
sendo que I é o momento de inércia do pêndulo em relação
ao ponto O.
15.6: Pêndulos
A aproximação usada para calcular a aceleração angular do
pêndulo simples consiste em supor que sen θ ≅ θ. Vamos
investigar até que valor de θ essa aproximação é razoável.
θ (graus)
θ (radianos)
sen θ
5
0,087
0,087 (erro < 1%)
10
0,174
0,174 (erro < 1%
15
0,262
0,259 (erro ≈ 1%)
20
0,349
0,342 (erro ≈ 2%)
Conclusão: O erro é menor que 1% para θ < 10°.
Exemplo: Pêndulo
Exemplo: Pêndulo (continuação)
15.7: MHS e movimento circular uniforme
Considere um ponto P' que descreve um
movimento circular uniforme com velocidade
angular ω.
A projeção do ponto P' no eixo x é um ponto
P cujo movimento pode ser descrito pela
equação
x(t ) = xm cos(ωt + ϕ ),
que é a equação do MHS.
O MHS é, portanto, a projeção do
movimento circular uniforme no diâmetro
da circunferência na qual acontece o
movimento circular.
15.8: MHS Amortecido
Em uma oscilação amortecida, o
movimento do oscilador é reduzido
por uma força externa.
Exemplo: Um bloco de massa m
oscila verticalmente preso a uma
mola de constante elástica, k. Uma
barra liga o bloco a uma placa
imersa em um líquido. O líquido
exerce uma força de arrasto sobre a
placa e, portanto, sobre todo o
sistema.
15.8: MHS Amortecido
A força de amortecimento, Fa, é muitas
vezes proporcional à velocidade v, ou
seja,
Fa = − bv
De acordo com a 2a lei de Newton, temos:
dx
d 2x
m 2 +b
+ kx = 0
dt
dt
cuja solução é
x (t ) = x m e
− bt
2m
cos(ω ' t + φ )
onde ω’ é a frequência angular, dada por
k
b2
ω' =
−
m 4m 2
15.8: MHS Amortecido
x (t ) = x m e
− bt
2m
cos(ω ' t + φ )
A figura mostra a função
deslocamento x(t) de um
oscilador amortecido. A
amplitude das oscilações
diminui exponencialmente
com o tempo.
Exemplo: MHS amortecido
Exemplo: MHS amortecido (continuação)
Exemplo: MHS amortecido (continuação)
15.9: Oscilações forçadas e ressonância
Quando um oscilador é submetido a uma força externa que
é periódica, passa a apresentar oscilações forçadas.
Exemplo: Um balanço empurrado por uma força periódica
de frequência angular ωe.
O comportamento de um oscilador submetido a oscilações
forçadas envolve duas frequências:
Ι. ω, a frequência angular natural do oscilador;
ΙΙ. ωe, a frequência angular da força aplicada.
15.9: Oscilações forçadas e ressonância
A ressonância acontece quando a
frequência das oscilações forçadas,
ωe, é igual à frequência natural ω.
Essa é a situação na qual a amplitude
da velocidade é máxima e também,
aproximadamente, a amplitude para a
qual o deslocamento é máximo. A figura
ao lado mostra a amplitude do
deslocamento em função da razão
entre as duas frequências.
Exemplo: Em setembro de 1985, muitos edifícios da Cidade do
México desabaram quando a cidade foi sacudida por um
terremoto. Isso aconteceu porque a frequência natural desses
edifícios estava próxima da frequência das ondas sísmicas.