LISTA DE EXERCÍCIOS – REVISÃO – FRENTE 3 – 1º TRI/17

LISTA DE EXERCÍCIOS – REVISÃO – FRENTE 3 – 1º TRI/17
1. (G1 1996) Um feixe de 4 paralelas determina sobre uma transversal três segmentos
consecutivos que medem 5 cm, 6 cm, 9 cm. Calcule os comprimentos do segmentos
determinados pelo feixe noutra transversal, sabendo que o segmento desta, compreendido
entre a primeira e a quarta paralela é 60 cm.
2. (G1 1996) O triângulo ABC da figura tem CM como bissetriz. Determine os lados do
triângulo.
3. (G1 1996) No ∆ da figura a seguir, DE//BC nessas condições determine:
a) a medida x
b) o perímetro do ∆ ABC
4. (G1 1996) Na figura a seguir, temos o segmento AD que é idêntico a CD e AB que é
idêntico a BC. Prove que o ângulo A é idêntico ao ângulo C.
5. (Cefet MG 2014) A figura abaixo tem as seguintes características:
- o ângulo Ê é reto;
- o segmento de reta AE é paralelo ao segmento BD;
- os segmentos AE, BD e DE, medem, respectivamente, 5, 4 e 3.
O segmento AC, em unidades de comprimento, mede
a) 8.
b) 12.
c) 13.
d) 61.
e) 5 10.
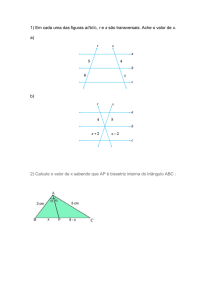
6. (G1 1996) Na figura a seguir, o valor de x é:
a) 18 cm
b) 20 cm
c) 22 cm
d) 24 cm
7. (G1 1996) Na figura a seguir, o valor de x é:
a) 6
b) 7
c) 8
d) 9
8. (G1 1996) Na figura a seguir, BA ll CD . Então x e y valem, respectivamente:
a) 25 cm e 13 cm
b)
16
4
e
3
3
c) 20 cm e 12 cm
d) 40 cm e 24 cm
9. (Fgv 2015) A figura representa um triângulo ABC, com E e D sendo pontos sobre AC.
ˆ mede 39.
Sabe-se ainda que AB  AD, CB  CE e que EBD
Nas condições dadas, a medida de ABC é
a) 102
b) 108
c) 111
d) 115
e) 117
10. (G1 - cftmg 2015) O perímetro do triângulo ABC vale 120 cm e a bissetriz do ângulo Â
divide o lado oposto em dois segmentos de 18 e 22cm, conforme a figura.
A medida do maior lado desse triângulo, em cm, é
a) 22
b) 36
c) 44
d) 52
11. (Uece 2014) No triângulo OYZ, os lados OY e OZ têm medidas iguais. Se W é um ponto do lado
OZ tal que os segmentos YW, WO e YZ têm a mesma medida, então, a medida do ângulo YÔZ é
a) 46°.
b) 42°.
c) 36°.
d) 30°.
12. (G1 - utfpr 2013) Um triângulo isósceles tem dois lados congruentes (de medidas iguais) e
o outro lado é chamado de base. Se em um triângulo isósceles o ângulo externo relativo ao
vértice oposto da base mede 130°, então os ângulos internos deste triângulo medem:
a) 10°, 40° e 130°.
b) 25°, 25° e 130°.
c) 50°, 60° e 70°.
d) 60°, 60° e 60°.
e) 50°, 65° e 65°.
13. (G1 - ifpe 2012) Júlia começou a estudar Geometria na sua escola. Com dúvida em um
exercício passado pelo professor de matemática, ela pediu ajuda ao seu tio. O enunciado era:
“As retas r e s são paralelas; as retas u e t, duas transversais. Encontre o valor do ângulo x na
figura abaixo”. Portanto, o valor de x é:
a) 120º
b) 125º
c) 130º
d) 135º
e) 140º
14. (Pucrj 2012) Considere um triângulo ABC retângulo em A, onde AB  21 e AC  20. BD
ˆ Quanto mede AD ?
é a bissetriz do ângulo ABC.
42
5
21
b)
20
20
c)
21
d) 9
e) 8
a)
15. (Uece 2010) No retângulo PQRS as medidas dos lados PQ e PS são, respectivamente, 15
m e 10 m. Pelo ponto médio, F, do lado PS traça-se o segmento FR dividindo o retângulo em
duas partes. Se E é o ponto do lado PQ tal que a medida do segmento EQ é 5 m, traça-se por
E uma perpendicular a FR determinando o ponto G em FR. Nestas condições, a medida da
área, em metros quadrados, do quadrilátero PFGE é
a) 50,25.
b) 53,25.
c) 56,25.
d) 59,25.
Gabarito:
Resposta da questão 1:
x = 15; y = 18; y = 27
Resposta da questão 2:
11, 11, 12
Resposta da questão 3:
a) 5
b) 35
Resposta da questão 4:
AB ≈ BD
AC ≈ CD
BC é comum
então (LLL):
∆ ABC ≈ ∆ DBC
logo  ≈ Ĉ
Resposta da questão 5:
[E]
Desde que os triângulos ACE e BCD são semelhantes por AA, vem
CD
CE

BD
AE

CD
CD  3

4
5
 CD  12.
Portanto, aplicando o Teorema de Pitágoras no triângulo ACE, encontramos
2
2
2
2
AC  AE  CE  AC  52  152
 AC  5 10.
Resposta da questão 6:
[D]
Resposta da questão 7:
[B]
Resposta da questão 8:
[D]
Resposta da questão 9:
[A]
Seja CBD  x. Logo, dado que CB  CE, vem CEB  x  39. Em consequência, usando o fato
de que a soma dos ângulos internos do triângulo BED é igual a 180, obtemos EDB  102  x.
Além disso, como AB  AD, segue que ABE  63  x. Portanto, a resposta é 102.
Resposta da questão 10:
[C]
a  b  40  120  a  b  80
Aplicando o Teorema da bissetriz interna, temos:
c
b
bc
c
b




 2  c  36 e b  44
18 22 18  22
18 22
Portanto, a medida do maior lado do triângulo é de 44cm.
Resposta da questão 11:
[C]
No ΔYWO : x  2  q (ângulo externo)
No ΔOYZ : q 2x  180  5  q  180  q  36
Logo,
YÔZ : 36 .
Resposta da questão 12:
[E]
Na figura y = 180° – 130° = 50°
130 = 2x  x = 65°
Portanto os ângulos internos do triângulo medem 50°, 65° e 65°.
Resposta da questão 13:
[E]
Traça-se u // r // s
y = 20° (correspondentes)
x = 120° + y (alternos internos)
x = 120° + 20°
x = 140°
Resposta da questão 14:
[A]
Admitindo AD  x.
BC2  202  212  BC  29
Utilizando o teorema da bissetriz interna, temos:
21
29
42

x
x
20  x
5
Logo, AD 
42
.
5
Resposta da questão 15:
[C]
PEF  QRE (l. A.L)
PEF  QRE ( H .C.)
1
. APFQR
2
1 (10 5).15
A .
2
2
A  56,25
log o
A