números complexos

UNIDADE X I
números complexos
31 Estudando números
CA P Í T U LO
Banco de questões
complexos
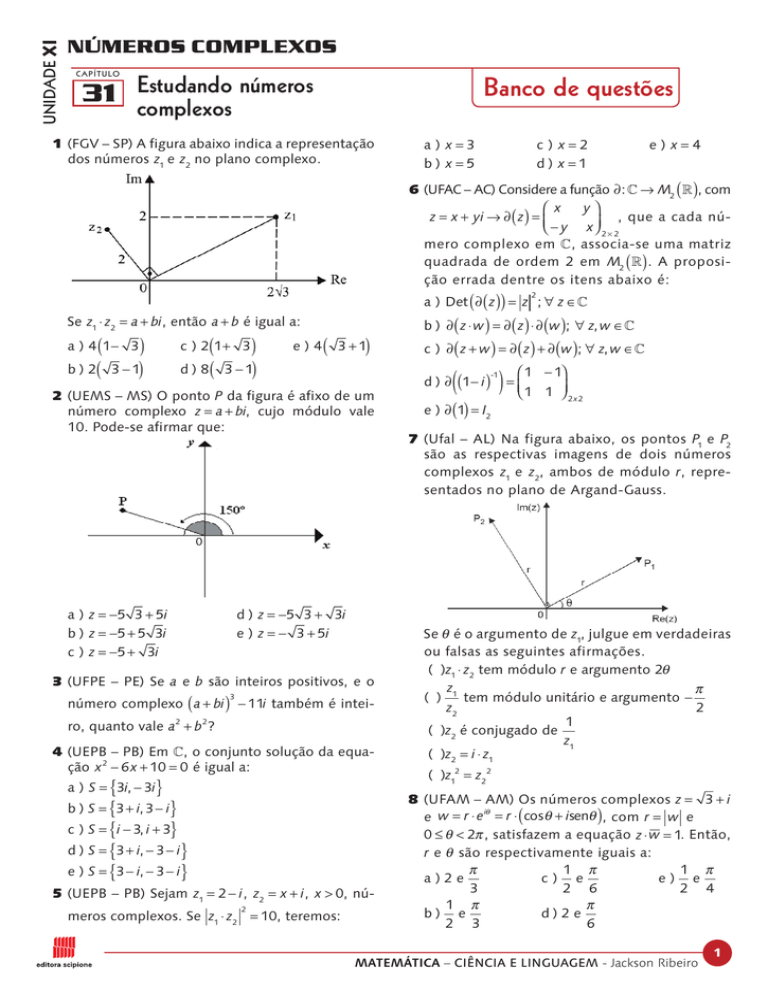
1(FGV – SP) A figura abaixo indica a representação
dos números z1 e z2 no plano complexo.
a)x = 3
b)x = 5
c)x = 2
d)x = 1
e)x = 4
6(UFAC – AC) Considere a função ∂ :  → M2 (  ), com
 x
y
z = x + yi → ∂ ( z ) = 
, que a cada nú − y x 
2× 2
mero complexo em , associa-se uma matriz
quadrada de ordem 2 em M2 (  ) . A proposição errada dentre os itens abaixo é:
a)Det ( ∂ ( z )) = z ; ∀ z ∈
2
Se z1 ⋅ z2 = a + bi, então a + b é igual a:
(
b)2(
)
3 − 1)
a)4 1− 3
(
d)8 (
)
3 − 1)
c)2 1+ 3
e)4
(
b) ∂ ( z ⋅ w ) = ∂ ( z ) ⋅ ∂ (w ); ∀ z, w ∈
)
c) ∂ ( z + w ) = ∂ ( z ) + ∂ (w ); ∀ z, w ∈
3 +1
2(UEMS – MS) O ponto P da figura é afixo de um
número complexo z = a + bi, cujo módulo vale
10. Pode-se afirmar que:
(
d)∂ (1− i )
-1
e)∂ (1) = I2
) =  11
− 1
1 
2x2
7(Ufal – AL) Na figura abaixo, os pontos P1 e P2
são as respectivas imagens de dois números
complexos z1 e z2, ambos de módulo r, representados no plano de Argand-Gauss.
0
a)z = −5 3 + 5i
b)z = −5 + 5 3i
c)z = −5 + 3i
d)z = −5 3 + 3i
e)z = − 3 + 5i
3(UFPE – PE) Se a e b são inteiros positivos, e o
número complexo ( a + bi ) − 11i também é intei3
ro, quanto vale a2 + b2 ?
4(UEPB – PB) Em , o conjunto solução da equação x 2 − 6 x + 10 = 0 é igual a:
a)S = {3i, − 3i}
b)S = {3 + i, 3 − i}
c)S = {i − 3, i + 3}
d)S = {3 + i, − 3 − i}
e)S = {3 − i, − 3 − i}
5(UEPB – PB) Sejam z1 = 2 − i , z2 = x + i , x > 0, nú2
meros complexos. Se z1 ⋅ z2 = 10, teremos:
Se θ é o argumento de z1, julgue em verdadeiras
ou falsas as seguintes afirmações.
( )z1 ⋅ z2 tem módulo r e argumento 2θ
z
π
( ) 1 tem módulo unitário e argumento −
2
z2
1
( )z2 é conjugado de
z1
( )z2 = i ⋅ z1
( )z12 = z22
8(UFAM – AM) Os números complexos z = 3 + i
iθ
e w = r ⋅ e = r ⋅ ( cosθ + isenθ ), com r = w e 0 ≤ θ < 2π , satisfazem a equação z ⋅ w = 1. Então,
r e θ são respectivamente iguais a:
π
1 π
1 π
c) e
e) e
a)2 e
3
2 6
2 4
1 π
π
b) e
d)2 e
2 3
6
MATEMÁTICA – CIÊNCIA E LINGUAGEM - Jackson Ribeiro
9(UFBA – BA) Na figura, tem-se uma circunferência de centro na origem dos eixos coordenados
e raio igual a 2 u.c. O comprimento do menor
arco de origem em A e extremidade em P1 é igual
π
a
u.c. Considere os pontos P1, P2 e P3 vértices
3
de um triângulo eqüilátero inscrito na circunferência e representados, nessa ordem, no sentido
anti-horário.
Sendo P1, P2 e P3, respectivamente, afixos dos números complexos z1, z2 e z3, calcule z1 + z25 + z3 .
10(UFC – CE) Ao dividir 1− 3i por −1+ i, obtém-se
um complexo de argumento igual a:
π
a)
4
5π
b)
12
7π
c)
12
3π
d)
4
11π
e)
12
11(UFMG – MG) Seja S o conjunto de números
complexos z, tais que z − ( 2 + 4 i ) = 2.
a)No plano complexo a seguir, faça o esboço de
S, sendo z = x + yi, com x e y números reais.
12(UFMT – MT) Dados os números complexos nãonulos z = a + bi e w = i ⋅ z. Sendo α e β os argumentos, respectivamente, de z e w, com 0 ≤ α < 2π e
0 ≤ β < 2π , pode-se afirmar que β − α é igual a:
π
2
π
b)
4
c)π
a)
3π
2
3π
e)
4
d)
13(UFRJ – RJ) Considere a equação
x 3 + 3x 2 + 9 x + 9 = 0 .
a)Fazendo x = y − 1, obtenha uma equação equivalente tendo y como incógnita. Em seguida,
2
faça y = z − e obtenha uma nova equação
z
em z.
b)Calcule todas as soluções para a equação em
z obtida no item a.
14(UFS – SE) Considere os números complexos u = i
e v = 1+ i para julgar em verdadeiras ou falsas as
seguintes afirmações.
( )Se m e n são números naturais distintos entre
si e tais que um = un, então m − n é múltiplo de
4.
( )O argumento principal do número complexo
u
é igual ao argumento principal de v.
v
( )Se z é um número complexo, tal que z + v = 3 2, então o menor valor de z é
igual a 2 2.
( )No plano de Argand-Gauss, as imagens dos
números complexos z, tais que z − u = z + v ,
pertencem a uma reta que contém a origem.
( )A diferença entre o conjugado de u e o conjugado de v é um número real positivo.
15(Ufscar – SP) Considere a equação algébrica
− x 4 + kx 3 − kx 2 + kx − 4 = 0, na variável x, com
k ∈.
a)Determine k = a + bi, com a e b reais, para que
o número complexo 2i seja uma das raízes da
equação.
b)Determine todas as raízes da equação quando k = 5.
b)Determine o ponto de S mais próximo da origem.
16(UFV – MG) A área do polígono cujos vértices
4
são as raízes complexas da equação ( z − 2) = −4
é igual a:
a)9
d)6
b)8
e)4
c)2
MATEMÁTICA – CIÊNCIA E LINGUAGEM - Jackson Ribeiro
17(Unesp – SP) Considere os números complexos
w = 4 + 2i e z = 3a + 4 ai, em que a é um número
real positivo e i indica a unidade imaginária. Se,
em centímetros, a altura de um triângulo é z e a
base é a parte real de z ⋅ w, determine a de modo
que a área do triângulo seja 90 cm2.
18(Unifor – CE) Seja o número complexo z = x + 3i,
em que x é um número real negativo. Se z = 6,
então a forma trigonométrica de z é:

2π
2π 
a)6  cos
+ i ⋅ sen 

3
3

5π
5π 
b)6  cos
+ i ⋅ sen 

6
6

4π
4π 
c)6  cos
+ i ⋅ sen 

3
3 

5π
5π 
d)6  cos
+ i ⋅ sen 

3
3

11π
11π 
e)6  cos
+ i ⋅ sen

6
6 
19(UESC – BA) Na forma trigonométrica, o número
2
1− i )
(
é representado por:
complexo z =
1+ i

π
π
a) 2  cos − i ⋅ sen 

4
4

π
π
b) 2  cos + i ⋅ sen 

4
4

5π
5π 
c) 2  cos
+ i ⋅ sen 

4
4

3π
3π 
d) 2  cos
+ i ⋅ sen 

4
4

7π
7π 
e) 2  cos
+ i ⋅ sen 

4
4
MATEMÁTICA – CIÊNCIA E LINGUAGEM - Jackson Ribeiro
Respostas do capítulo 31
1a
2a
35
4b
5d
6d
7F, V, F, V, F
8c
932
10e
11a )
 5
5
b ) z = 2 5 − 2 
+ 2i
5 
 5
(
)
12a
13a ) y 3 + 6 y + 2 = 0 e z 3 + 2 −
8
=0
z3
 1
 1
3 
3 
b)z = 3 2, z = 3 2  − +
i , z = 3 2  − −
i ,
 2 2 
 2 2 
1
1
3 
3 
z = − 3 4, z = 3 4  +
i e z = 3 4  −
i
2 2 
 2 2 
14V, V, V, F, F
20 30
+
i
13 13
b)S = {− i, i, 1, 4}
15a ) k =
16e
17 a = 3 cm
18b
19c
MATEMÁTICA – CIÊNCIA E LINGUAGEM - Jackson Ribeiro