pH e Soluções-tampão

pH e Soluções-tampão
Universidade Federal do Ceará
Centro de Ciências
Departamento de Bioquímica e Biologia Molecular
Disciplina de Biofísica
pH e soluções-tampão
1. Lei de Ação das Massas – Equilíbrio Químico
2. Dissociação da água
3. pH
4. Ácidos e Bases Fracas
5. Soluções-tampão
6. Equação de Henderson-Hasselbalch
7. Curvas de Titulação
8. Importância do pH nos sistemas biológicos
pH e Soluções-tampão
pH e Soluções-tampão
1. Lei de Ação das Massas – Equilíbrio Químico
Enunciado:
“A velocidade de uma reação é proporcional ao produto de concentração
ativa das substâncias que reagem”
Então:
V ∝ [C1 ].[C2 ].[C3 ]...[Cn ]
Adicionando uma constante, teremos:
V = K [C1 ].[C2 ].[C3 ]...[Cn ]
Tomando como exemplo a seguinte reação:
V1
A+B
C+D
V2
No ponto de equilíbrio:
• As velocidades de ida e volta são iguais e constantes;
• As massas de A, B, C e D ficam constantes, mas não necessariamente
iguais.
Então:
V1 = K1 [ A].[ B]
e
V2 = K 2 [C ].[ D]
Portanto, no equilíbrio:
V1 = V2
Então:
K1 [ A].[ B] = K 2 [C ].[ D]
Rearranjando a equação, teremos:
pH e Soluções-tampão
K eq. =
K1 [ A].[ B]
=
K 2 [C ].[ D]
Então temos que a constante de equilíbrio:
K eq. =
[ produtos]
[reagentes]
2. Dissociação da Água
As moléculas de água têm uma leve tendência a sofrer ionização reversível
para produzir íon hidrogênio e a hidróxido, dando o equilíbrio:
H2O
H+ + OH-
[ H + ][OH − ]
K eq. =
[ H 2O]
• Água Pura, 25 oC → [H2O] = 55,5 M → Constante
K eq.
[ H + ][OH − ]
=
55,5 M
(55,5) ⋅ K eq. = [ H + ] ⋅ [OH − ] = K w
Kw → Produto Iônico da Água
• Na água pura, a Keq. Foi mensurada por condutividade elétrica:
o 1,8 . 10-16 M 25 oC
• Portanto:
(55,5M ) ⋅ K eq. = [ H + ] ⋅ [OH − ]
55,5M ⋅ (1,8 ⋅ 10−16 M ) = [ H + ] ⋅ [OH − ]
99,9 ⋅ 10−16 M 2 = 1 ⋅ 10−14 M 2 = [ H + ] ⋅ [OH − ]
Como na água pura a [H+] = [OH-]:
[ H + ] = K w ⇔ [ H + ] = [OH − ] = 10−7 M
3. pH
• O produto iônico da água é a base para a escala de pH;
pH e Soluções-tampão
• pH (Potencial Hidrogeniônico) é um meio conveniente de designar a [H+]
em qualquer solução aquosa variando entre 1M H+ e 1M de OH-;
• Escala de 1 a 14;
pH = log
1
= − log[H + ]
+
[H ]
• Portanto o pH da água pura é: [H+] = 1 . 10-7 M ⇔ pH 7,0
• Escala de pH:
4. Ácidos e Bases Fracas
• Ácidos e Bases fortes:
o Completamente ionizados em solução aquosa
H+ + A -
HA
e
XOH
X+ + OH-
• Ácidos e Bases Fracas:
o Não se dissociam completamente em solução aquosa
H+ + A -
HA
e
XOH
X+ + OH-
• Conceito de Bröwsted-Lowry:
o Ácido → Qualquer substância que libera prótons H+;
o Base → Qualquer substância que aceita prótons H+.
• Uma substância doadora de prótons e seu aceptor correspondente de
prótons fazem o que se chama de par conjugado ácido-base. Portanto,
para um ácido qualquer:
HA
H+ + A -
Ácido
Base
[ H + ][ A− ]
Kα =
[ HA]
pH e Soluções-tampão
• Para reações de ácido e base, as constantes de equilíbrio são comumente
chamadas de constantes de dissociação, Ka;
• Ácidos fortes possuem alta Ka e ácidos fracos possuem baixa Ka;
• De forma análoga ao pH, pKa é:
pK a = log
1
= − log K a
Ka
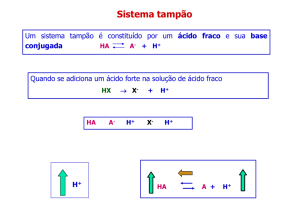
5. Soluções-tampão
• Definição:
“São sistemas aquosos que tendem a resistir mudanças no seu pH quando
pequenas quantidades de ácido (H+) ou base (OH-) são adicionadas”
• Consiste de um ácido fraco e sua base conjugada ou uma base fraca e seu
ácido conjugado;
• O tamponamento resulta do equilíbrio entre duas reações reversíveis
ocorrendo em uma solução com uma concentração de um doador de
prótons e seu aceptor conjugado aproximadamente iguais;
• Sempre que H+ ou OH- são adicionados ao tampão, o resultado é uma
pequena mudança na razão das concentrações relativas do ácido fraco e
seu ânion e portanto uma pequena mudança de pH;
• O decréscimo na concentração de um componente do sistema é
balanceado exatamente por um aumento no outro;
• A soma dos componentes do tampão não muda apenas sua razão.
6. Equação de Henderson-Hasselbalch
• Relação quantitativa entre o pH, a ação tamponante de uma mistura de
um ácido fraco e sua base conjugada e o pKa do ácido fraco:
[ H + ][ A− ]
Kα =
[ HA]
[ H + ] = Kα
[ HA]
[ A− ]
pH e Soluções-tampão
Aplicando logaritmo negativo em ambos os lados, teremos:
− log[H + ] = − log K a − log
pH = pK a − log
[ HA]
[ A− ]
[ HA]
[ A− ]
Invertendo o logaritmo:
[ A− ]
pH = pK a + log
[ HA]
Concluindo, temos que:
pH = pK a + log
[ Aceptor de prótons]
[ Doador de prótons]
• Essa equação possibilita:
o O cálculo do pKa de qualquer ácido a partir da razão molar de
doador e aceptor de prótons em qualquer pH;
o Calcular o pH de um conjugado ácido-base de um pKa conhecido;
o Calcular a razão molar de um doador e aceptor de prótons em
qualquer pH, dado o pKa do ácido fraco.
• Extremamente útil nos cálculos para preparo de tampões;
• Faixa de tamponamento mais efetiva: pH = pKa ± 1.
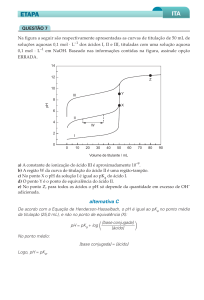
7. Curvas de Titulação
• Ácido Fraco;
• Aminoácido.
8. Importância do pH nos Sistemas Biológicos