2, a partir do ponto O.

9º
Geometria
Júnior
Aval. Trimestral
04/07/12
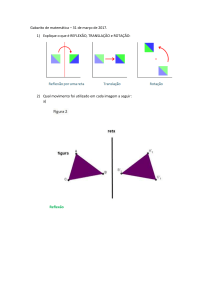
1. Homotetia
Transformação por homotetia.
Homotetia é a ampliação ou a redução de distâncias e
áreas a partir de um ponto fixo. Uma homotetia é definida
pelo seu centro O e pela razão k de homotetia e é a
aplicação afim tal que a cada ponto P faz corresponder o
ponto P' tal que:
O termo é devido ao matemático francês Michel Chasles,
em 1827, derivado do grego como composto de homo
(similar) e tetia (posição).
Uma homotetia preserva:

os ângulos,

as razões entre os segmentos de reta e

o paralelismo.
obs.: Duas figuras homotéticas possuem a mesma forma e seus lados correspondentes
(homologos) são paralelos dois a dois . Embora as figuras possuam a mesma forma , seus lados
não possuem necessariamente a mesma medida , mas, como houve uma redução ou ampliação
numa mesma razão , eles são proporcionais .
Baseado no texto acima construa duas figuras homotéticas à figura dada nas
razões k = 3/2 e k = -2, a partir do ponto O.

o
2. Assinale V (verdadeira) ou F (falsa) para as sentenças. Se necessário, faça
desenhos para representar as situações dadas.
(
) Dois quadrados são sempre semelhantes.
(
) Dois triângulos são sempre semelhantes.
(
) Dois triângulos isósceles são sempre semelhantes.
(
) Dois triângulos equiláteros são sempre semelhantes.
(
) Duas circunferências são sempre semelhantes.
(
) Dois paralelepípedos são sempre semelhantes.
(
) Dois cubos são sempre semelhantes.
(
) Dois retângulos são sempre semelhantes.
3. Existe o caso de semelhança LLL? Ou seja, se dois triângulos possuírem os
lados respectivamente proporcionais, seus ângulos correspondentes serão
congruentes, garantindo a semelhança entre os dois triângulos?
Construa com compasso os pares de triângulos indicados e com auxílio do
transferidor, meça os ângulos correspondentes e verifique se são congruentes.
a) 2 cm , 3 cm e 4 cm
b) 4 cm , 6 cm e 8 cm
4. Justifique por que dois triângulos isósceles são semelhantes.
5. Segurando verticalmente, à sua frente, uma régua de 30 cm de comprimento,
você verifica que é possível alinhar a extremidade superior da régua com o topo
da cabeça e a extremidade inferior da régua com a ponta dos pés de uma amiga
a 2,70 m de distância.
Se a distância entre a régua e seus olhos é de 50 cm, qual é a altura de sua
amiga?
6. No triângulo ABC, C é um ângulo reto e CD é altura relativa à hipotenusa.
Construa esse triângulo e responda as seguintes perguntas:
a) Dê o nome de um ângulo congruente ao ângulo ACB.
b) Dê o nome de um ângulo congruente ao ângulo CBA.
c) Dê o nome de um triângulo semelhante ao triângulo ABC. Descreva a
semelhança entre esses triângulos.
7. São tiradas duas fotocópias de um original, uma do mesmo tamanho do original
e a outra ampliada. Na primeira cópia, um objeto tem largura de 2 cm e altura de
2,4 cm. Na ampliação, o objeto tem largura de 7,5 cm. Qual é sua altura na
ampliação?
8. Um prédio tem sombra, pela luz solar, projetada no solo horizontal com 70 m.
Simultaneamente um poste de 8m de altura localizado nas proximidades deste
prédio também tem sua sombra projetada no solo. Sabendo que neste instante
os raios solares fazem um ângulo de 45° com o solo, calcule a altura do prédio e
a sombra do poste.
9. Calcule o valor de x na figura, sendo r//s//t.
10. Calcule o valor de x na figura, sendo r//s//t.