Exame 20-01-12 com Resolucao

Engenharia do Ambiente
Mecânica dos Fluidos Ambiental (1º semestre, 3º ano)
(Primeiro Exame, 20 de Janeiro de 2011)
Duração 2h30 horas. Justifique todas as respostas.
Problema I (13 valores)
B
A
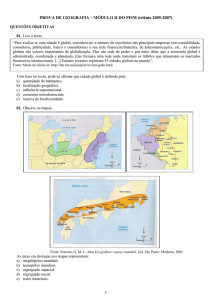
Fig. 1 – Escoamento numa tubeira (contracção seguida de expansão).
A figura - retirada de um livro de Mecânica dos Fluidos - representa um escoamento ar numa contracção
seguida de uma expansão. A linha a tracejado pretende representar a camada limite, que se separa da parede
na expansão, formando duas zonas de recirculação. Na secção do ponto A o diâmetro são 10 cm e na
garganta são 5 cm.
a) Represente esquematicamente as linhas de corrente que passam nos pontos A e B. (1 val)
b) Represente esquematicamente a evolução da pressão entre a secção de entrada e de saída, ao longo da
linha central. Se não tivesse ocorrido separação, a pressão na secção do ponto B seria maior ou menor?
(2 val)
c) Tendo em consideração a forma das linhas de corrente e a evolução de pressão ao longo da linha central,
diga em que pontos é mínima a pressão (1 val)
d) Represente esquematicamente o perfil das tensões de corte na secção do ponto A e na garganta. (1.5 val)
e) Desprezando o efeito da camada limite (admitindo que o escoamento é invíscido em todo o domínio)
calcule o caudal se a pressão em A for 1.2*104Pa e na garganta for 104Pa. (2 val)
f) Calcule a força exercida pelo escoamento sobre a conduta entre as secções do ponto A e a garganta. (se
não resolveu a alínea anterior considere um caudal de 0.1 m3/s) (2 val)
g) Escreva a equação de Navier Stokes para a zona exterior da camada limite e diga como varia o termo
advectivo ao longo do eixo da conduta. (1.5 valores)
h) Escreva a equação de Navier Stokes para o interior da camada limite. (1 val)
i) Efectivamente as linhas que pretendem representar a camada limite estão pouco cuidadas, não sendo
sempre consistentes com a forma dos perfis de velocidades representados. Diga onde são inconsistentes.
(1 val)
Problema II (2 valores)
A resistência ao movimento de um corpo com 20 cm de largura e área frontal de 20 cm2 foi medida em
escoamentos de ar de várias velocidades tendo sido obtidos os resultados seguintes:
Velocidade (m/s)
10
16
21
Força de Resistência (N)
5.0
12.8 22.1
Diga se a solução é independente do nº de Reynolds ou se precisaria de fazer ensaios a Reynolds mais
elevados.
Problema III (5 valores)
A figura mostra esquematicamente um reservatório que despeja água através de um tubo de 5 metros de
comprimento e 3 cm de diâmetro, com rugosidade de 0.2 mm.
a) Calcule o caudal descarregado se a água fosse um fluido ideal. (2 val)
b) Calcule o caudal descarregado considerando atrito no tubo, mas desprezando a perda de energia na
entrada. Admita que o escoamento é completamente turbulento (2val)
c) Indique um algoritmo que lhe permitiria calcular o caudal sem admitir que o escoamento é
completamente turbulento (1 val)
Resolução
NOTA: a figura I que está neste enunciado não é exactamente a mesma que foi impressa. Desconfigurou-se
para a impressão… Apresento esta resolução para ficar para anos subsequentes.
PROBLEMA I
a)
O caudal entre duas linhas de corrente mantém-se constante. Entre a linha a vermelho e a parede tem que se
manter constante porque a parede é uma linha de corrente. A linha aproxima-se da parede até à contracção e
afasta-se da parede na expansão. A espessura da camada limite na figura varia pouco e por isso não parece
que a linha Nesta figura a espessura da camada limite varia pouco e por isso a linha de corrente não deveria
entrar na camada limite. A linha a azul (ponto A do enunciado) está dentro da camada limite e não pode sair.
Depois da separação mantém-se entre a linha que limita a camada limite e a linha de corrente que “nasce” no
ponto de separação. A linha a verde inicia-se entre a linha de que delimita a separação e a parede e tem que
se manter aí.
b)
Este escoamento tem uma zona invíscida, onde podemos aplicar a equação de Bernoulli e uma zona onde os
efeitos viscosos são importantes (camada limite onde não a podemos aplicar), sendo em cada secção a
pressão no interior da camada limite igual à pressão fora da camada limite. A pressão diminui até à garganta,
enquanto a velocidade está a aumentar e diminui na expansão onde a velocidade diminui. Depois da
separação da camada limite a velocidade (na zona invíscida) deixa de baixar e a pressão permanece
aproximadamente constante.
d) A pressão mínima é na garganta, onde a velocidade é máxima. Na garganta a pressão é menor nos
pontos próximos da parede, devido à curvatura das linhas de corrente. Para equilibrar a força
centrífuga, a pressão é menor do lado de dentro da curva.
e) Temos que aplicar os principios da conservação da energia e da conservação da massa (Bernoulli e
equação da continuidade, que neste caso se reduz à constância do caudal em todas as secções).
1
1




2
2
 p  U  gz    p  U  gz 
2
2

A 
B


D 2 
D 2 
U *
  U *

4 A 
4  B

1
1


2
2
 p  U    p  U 
2
2

A 
B
UA UB
UB 
DB2
D A2
 p A  pB 
2
1   DB2  

 1 
2   D A2  



D1
D2
1.2
0.1
0.05
A1
A2
0.00785
0.001963
P1
P2
1.20E+04
1.00E+04
U2
U1
Q
59.62848
14.90712
0.117021
f) A força exercida sobre o escoamento pode é calculada usando o principio da conservação da
quantidade de movimento. Sendo o escoamento estacionário, a variação do fluxo de quantidade de
movimento na contracção é igual ao somatório das forças aplicadas: Designado a Entrada por “E” e a
saída (garganta) por “S”:
 QMS   QME  PAE  PAS  F
DS2
DE2
QV S  QV E  PE 
 PS 
F
4
4
0.12
0.05 2
0.117 * (59.6  14.9)  1.2 *10 4 
 1.0 *10 4 
F
4
4
F  69.3N
g) O escoamento é hirozontal e por isso não existem forças mássicas. No exterior da camada limite não
existem efeitos viscosos. Então a aceleração do fluido é exclusivamente devida à força de pressão.
Como o escoamento é estacionário, a aceleração é exclusivamente convectiva e o termo convectivo é
simétrico do gradiente de pressão. Ao longo da linha central a velocidade só tem componente axial e
a equação reduz-se à terceira equação abaixo. Nas outras linhas de corrente há velocidade
perpendicular ao eixo e por isso a equação tem também termo advectivo segundo x2.

du i
p

dt
xi
u j
u i
p

x j
xi
u1
u1
p

x1
x1
h) h)
No interior da camada limite aplica-se tudo o que se disse atrás, mas temos que juntar o termo difusivo.
du
u
p

 i 

 i
dt
xi x j x j
i) Efectivamente a linha que delimita a camada limite está pouco cuidada na figura. A camada limite
contém o fluido cuja veloicidade foi reduzida pelo atrito devido à parede. No terceito perfil há fluido
com velodidade reduzida que está fora da linha da camada limite. A este argumento poderiam ainda
juntar-se outros que transcendem o que se pretende neste exame, e.g. na contracção a camada limite
tende a diminuir de espessura devido à aceleração promivida pelo gradiente favorável de pressão e na
expansão o crescimento é maior.
PROBLEMA II
Calculando o coeficiente de resistência utilizando as velocidades e as forças, verificamos que é constante,
apesar de o Reynolds ir aumentando com a velocidade. Isso significa que estamos numa zona onde o
Reynolds já não é importante.
V (m/s)
F (N)
Re
10
5.0
0.00002
Cd
13
8.5
16
12.8
19
18.1
21
22.1
L
0.2 m
A
0.02 m2
0.000026 0.000032 0.000038 0.000042
4.166667 4.166666667 4.166667 4.166667 4.166667
PROBLEMA III
a) Não havendo atrito toda a energia potencial do fluido se vai converter em energia cinética. A equação
de Bernoulli terá como única incógnita a velocidade na saída:
1
1




2
2
 p  U  gz    p  U  gz 
2
2

A 
B
U  2 gh  2 *10 * 4  8.8m / s
m/s
Q  U
D2
0.03 2
 8.8 * 3.14 *
 0.006m 3 / s
4
4
b)
No caso de o escoamento ser completamente turbulento, o coeficiente de atrito só depende da rugosidade
relativa. Havendo atrito temos que considerar o termo de perda de carga na equação de Bernoulli. Neste caso
1
1
L 1




2
2
2
 p  U  gz    p  U  gz   4 f * U
2
2
D
2

A 
B
U
2 gh
2 * 10 * 4

 7.2m / s
L 1
5 


1 4 f * 
1   0.032

D 2
0.03 


D2
0.03 2
 28.3 * 3.14 *
 0.005m 3 / s
4
4
c) Neste caso teria que verificar a hipótese de que o escoamento é completamente turbulento. Se
começasse por admitir que é, poderia calcular a velocidade com o na alínea anterior. Sabendo a
Q  U
velocidade poderia calcular o Reynolds e poderia verificar a hipótese de turbulência completa. Se não
fosse calcularia um novo coeficiente de atrito e iniciaria um processo iterativo. Neste caso
Re=2.1*105 e estamos mesmo mo limite da zona completamente turbulenta. Se tivéssemos obtido e.g.
Re=104 teríamos que fazer o tal processo iterativo.