Objectivos Formulário

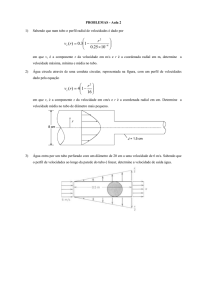
Objectivos
o
Determinar experimentalmente e relacionar entre si a resistência aerodinâmica
de corpos não-fuselados e a distribuição de pressão que actua na sua
superfície;
o
Verificar a vantagem de exprimir os resultados obtidos sob a forma de números
adimensionais e a sua baixa dependência do número de Reynolds, na gama de
valores utilizados nos ensaios efectuados;
o
Relacionar a resistência a distribuição de pressão com a forma dos diversos
corpos e a dimensão da esteira que neles se forma.
Formulário
Cálculo do Número de Reynolds
Re =
ρUL VL Vd
=
=
μ
ν
ν
, em que:
ρ - Densidade do fluido do escoamento [ kg / m 3 ]
U - Velocidade do escoamento [ m / s ]
L - Dimensão característica do corpo [ m ]
μ - Viscosidade dinâmica [ kg /(ms ) ]
ν - Viscosidade cinemática [ m 2 / s ]
Cálculo da Velocidade de Aproximação
Da equação de Bernoulli, obtém-se a seguinte igualdade:
p
1
+ V 2 + gz = Cte , obtendo-se assim:
ρ 2
Pdinâmica =
1
⋅ρ ar ⋅V 2
2
Finalmente, a velocidade pode-se expressar pela seguinte equação:
V =
2
ρ ar
⋅ Pdinâmica
Cálculo da Força de Resistência
O cálculo da força de resistência pode-se fazer através da integração da distribuição
de pressões na superfície do corpo através da expressão:
R
D pressão = 2π ∫ Δp ⋅ r ⋅ dr
0
D pressão
r1
r2
R
⎛
⎡r2 ⎤
⎡r2 ⎤
⎡ r 2 ⎤ ⎞⎟
⎜
= 2π Δp1 ⎢ ⎥ + Δp 2 ⎢ ⎥ + Δp3 ⎢ ⎥
⎜
⎣ 2 ⎦0
⎣ 2 ⎦ r1
⎣ 2 ⎦ r2 ⎟⎠
⎝
, em que r = 0, r 1 e r 2 são os
raios onde as tomadas de pressão foram lidas.
Δpi é a diferença de pressão resultante das medições efectuadas a montante e a
jusante de um corpo, para um mesmo raio, e para uma velocidade definida.
Em alternativa poder-se-á calcular a força de resistência através do balanço do
momento em torno do cutelo através da expressão:
Dmomento =
m ⋅ g ⋅ (L2 − L1 )
H
m - Massa deslocada para equilibrar o sistema [ kg ]
g - Aceleração gravítica [ m / s 2 ]
L1 - Afastamento em equilíbrio, sem jacto [ m ]
L2 - Afastamento, com jacto [ m ]
H - Distância do cutelo ao corpo [ m ]
DESENHOS
Coeficientes de Resistência
O coeficiente de resistência é dado pela expressão:
CD =
D
1
ρV 2 AFrontal
2
, em que o D, ou seja, a força de resistência é o valor
calculado através das duas formas possíveis, acima mencionadas.
D - Força de resistência
ρ - Densidade do fluido do escoamento
V - Velocidade do escoamento
AFrontal - Área frontal do corpo
Coeficientes de Pressão
No ensaio do cilindro 2D é possível exprimir o coeficiente de pressão através da
seguinte expressão:
CP =
p − p∞
1
ρU ∞2
2
, em que p − p ∞ a diferença de pressão entre a tomada e a
pressão atmosférica.
Discussão dos Resultados e Conclusões