Enunciado

Teste 1 Mecânica e Ondas
Licenciatura em Engenharia Mecânica + Naval
Data: 12 -4- 2007
Duração: 1h+30min
I (6 valores)
Duas réguas, cada uma das quais com comprimento próprio L0=50 cm, movem-se
longitudinalmente ao longo do eixo dos XX em sentidos contrários, com uma
velocidade v1=0.8c e outra com velocidade v2=0.9c.
Determine a velocidade da primeira régua no referencial próprio da segunda régua.
Determine o comprimento da primeira régua no referencial próprio da segunda régua.
v V
V
1
x    ( x  Vt )
t    (t  2 x)
v x  x

vV
c
V2
(1  x 2 )
1

c
c2
II (12 valores)
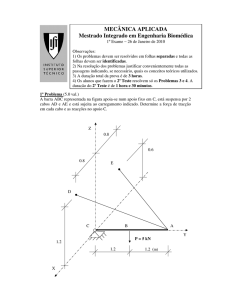
Um bloco de massa mA = 20 kg desliza ao longo duma superfície com atrito, μ=0.2. O
bloco está ligado por um fio de massa desprezável a outro de massa mB =5 kg, como
mostra a figura 1. O bloco vertical cai e as massas partem do repouso.
a) Faça um diagrama de forças do sistema. (1 val)
b) Escreva uma equação que exprime a restrição ao movimento das massas. Utilize as
coordenadas sugeridas na figura 1. (2 val)
c) Com base no diagrama de forças, escreva as equações de Newton para o sistema. (2
val)
d) Determine a aceleração de cada bloco. (1 val)
e) Obtenha uma expressão para a velocidade da massa mB quando esta cai uma distância
Δy. (2 val)
f) Escreva expressões para os diversos trabalhos e energias do sistema. (2 val)
A partir do balanço de energia obtenha a velocidade da massa mB quando esta cai uma
distância Δy. (2 val)
N.B.: As respostas deverão vir expressas em termos de mA, mB, μ, e g.
III (2 valores)
Um bloco de massa m desliza sem atrito sobre uma mesa horizontal. A massa está
constrangida a mover-se dentro de um anel de raio L, fixo à mesa. No instante t=0, o
bloco está a mover-se na tangencial no interior do anel com velocidade v0 como mostra
a figura 2. O coeficiente de atrito entre o bloco e o anel é μ.
Mostre que a velocidade do bloco para qualquer instante t>0 é dada por
 
r  rr

v0
 
x n 1
.(2 val) C. Polares: v  rr  r
;  x n dx 
v(t ) 
n 1
1  (  v 0 t / L)



a  (r  r 2 )r  (r  2r)
Figura 1
Figura 2