FTC 5 lista de variaveis

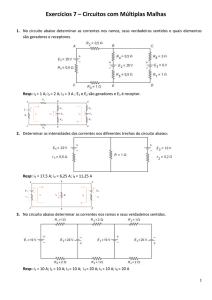
CEFET-BA
CURSOS DE ENGENHARIA – ANÁLISE DE VARIÁVEIS COMPLEXAS
PROFESSORA: EDMARY BARRETO
5a lista de exercícios
1) Encontre  f ( z )dz onde  é o círculo unitário e f(z) =

z2  1
.
( z  2)(2 z  1)2 (2 z  1)
2i
Resp. : 
.
15
2) Determine os resíduos de f ( z ) 
Resp. : 
( z  1) 2 ( z 2  4)
.
14 7  i
.
,
25 25
3) Calcule
Resp. :
z 2  2z
1
e zt 2
dz ao longo do círculo, cuja equação é z  3.
2i C z 2 ( z 2  2 z  2)

t  1 1 t
 e cos t .
2
2
4) Para cada uma das funções seguintes, determine os pólos e os correspondentes resíduos:
a)
2z  1
z z2
2
 z 1
b) 

 z 1
c)
sen( z )
z2
Resp.: z = -1, 2;
2
Resp.: z = 1; 4·
Resp.: 0; 1
1 5
,
3 3
Integrais Reais
2
 f (cos , sin )d
e i  z
d 
0
1
1
cos  ( z  )
2
z
1
dz
iz
sin 
1
1
(z  )
2i
z
2
 f (cos , sin )d  g ( z)dz , onde C é o contorno
0
z  1 e g(z) é a expansão obtida .
c
2

Exercícios: Encontre:
0

 f ( x)dx =

2
2
d
. Resp:
.
3  2 cos 
5
2)
d
 3  2 cos   sen 
Resp: 
0
R
lim
R 
 f ( x)dx
onde F(x) é uma função racional real cujo denominador tem grau no
R
mínimo 2 vezes maior que o numerador e onde o denominador de F(x) é diferente de zero para todo x real.

R
f ( z )dz 

f ( x)dx 
R
C


f ( z )dz
Temos no infinito
 f ( x)dx =2 i (soma dos resíduos de f(z) no meio

C1
plano superior)

Exemplo:
dx
 (1  x

2 3
)
dx 
3
8
Inversão das transformadas de Laplace

A transformada de Laplace de uma função f(t), dada por F(s) =
 f (t ) e
 st
dt tem um inverso f(t) =
0
1
2i
a 1
 F ( s )e
st
ds onde a integral é tomada ao longo de uma linha paralela ao eixo imaginário; s sendo
a i 
complexo. O número real a é escolhido de forma que todas as singularidades de F(s) estejam à
esquerda da linha de integração paralela ao eixo imaginário.
 F ( s )e
st
ds , onde C é o contorno de Bromwich no plano s
C
Exemplo: Seja q(t) a carga em um circuito utilizado para carregar um capacitor. Com a notação usual,
a transformada de Laplace da carga, a saber, Q(s) é dada por Q(s) =
1
2i
a i 

a  i
V0 e st
1
Rs( s 
)
RC
dt
q(t) = V0 C (1  e

t
RC
)
V0
1
{Rs[
 s ]}
RC
q(t) =