Lista_de_Exercícios-Derivadas

DISCIPLINA: Cálculo Diferencial e Integral I.
CURSO:
PROFESSOR:
DATA:
NOME:
TURMA:
L ISTA
DE
/
/
E XERCÍCIOS - D ERIVADAS
(Atualizada em 27 de abril de 2012)
"A ciência humana de maneira nenhuma nega a existência de Deus. Quando considero quantas e quão
maravilhosas coisas o homem compreende, pesquisa e consegue realizar, então reconheço claramente
que o espírito humano é obra de Deus, e a mais notável." Galileu Galilei
Derivadas
Definição
f ′ (x ) =
f (x + ∆x ) − f (x )
f (x ) − f (x0 )
dy
= lim
= lim
.
x
→
x
∆x
→0
dx
∆x
x − x0
0
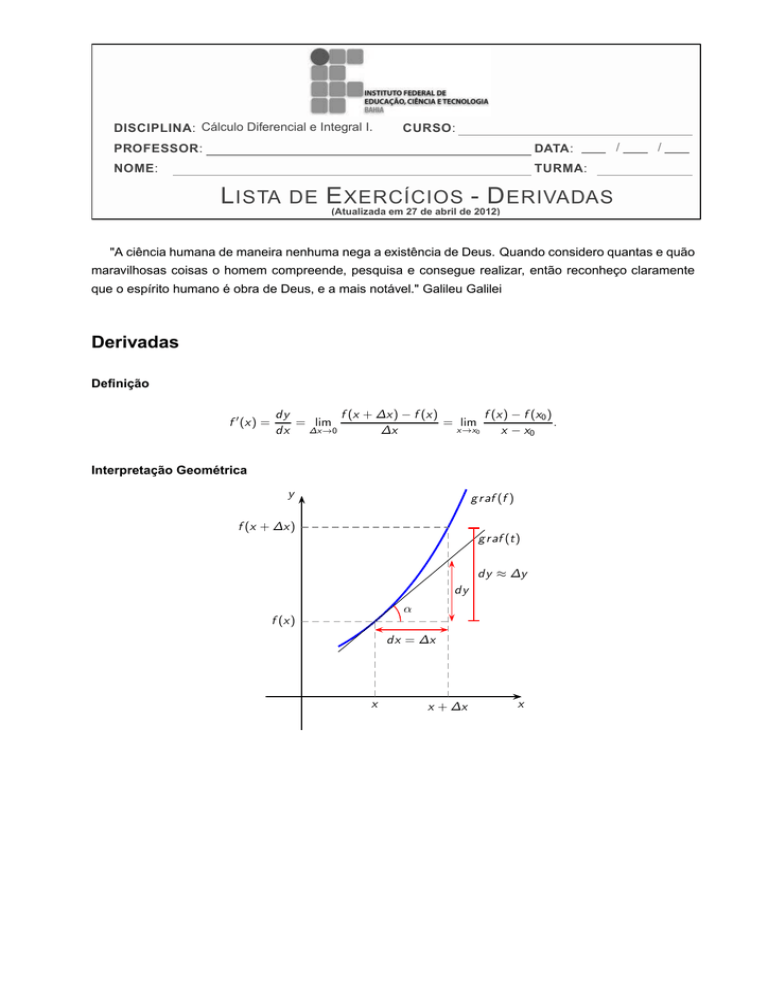
Interpretação Geométrica
y
g r af (f )
f (x + ∆x )
g r af (t )
dy
dy ≈ ∆y
α
f (x )
dx = ∆x
x
x + ∆x
x
http://aluloifbaonquista.webnode.om.br
Derivadas Imediatas
8. (sec(x ))′ = tg(x ) · sec(x );
1. k ′ = 0, ∀ k ∈ C;
9. (cossec(x ))′ = cotg(x ) · cossec(x );
1
10. (loga x )′ =
, ∀x ∈ R∗+ , 0 < a 6= 1,
x · ln(a)
1
em particular, (ln x )′ = ;
x
1
′
11. (arcsen x ) = √
;.
1 − x2
−1
12. (arccos(x ))′ = √
;
1 − x2
1
;
13. (arctg(x ))′ =
1 + x2
2. (x n )′ = nx n−1 ;
3. (ax )′ = ax · ln(a),
em particular, (e x )′ = e x ;
4. (sen(x ))′ = cos(x );
5. (cos(x ))′ = − sen(x );
6. (tg(x ))′ = sec2 x ;
7. (cotg(x ))′ = − cossec2 x ;
Regras da derivação
 ‹
1. d (f ± g ) = df ± dg ;
2. d (f · g ) = f · dg + g · df ;
3. d
f
g
=
g df − f dg
.
g2
Equações das Retas Tangente e Normal
1. Reta TANGENTE: y − f (a) = f ′ (a)(x − a);
2. Reta NORMAL: y − f (a) =
−1
(x − a).
f ′ (a)
Derivada da Função Composta
h(x ) = f (g (x )) ⇒ h′ (x ) = [f (g (x ))]′ · g ′ (x ).
Derivada da função inversa
y −1 =
1
1
⇒ (y −1 )′ = ′
.
f (x )
f (x )
Derivada da função exponencial composta
y = [u (x )v (x ) ] ⇒ y ′ = v · u v −1 · u ′ + u v · v ′ · ln x .
Definição, Interpretação Geométrica e Regras Operacionais
1. Usando a definição, determine a função primeira derivada e as derivadas nos pontos indicados.
(a) f (x ) = x 2 − 1, f ′ (0) e f ′ (1)
L ISTA DE E XERCÍCIOS C ALC 1 #
C ÁLCULO D IFERENCIAL E I NTEGRAL I
2
http://aluloifbaonquista.webnode.om.br
(b) f (x ) = x 2 − 3x + 6, f ′ (−1) e f ′ (2)
 ‹
(c) f (x ) =
1 ′ 1
,f
x
3
e f ′ (3)
(d) f (x ) = sen(x ), f ′ (0), f ′
π 2
e f ′ (π)
2. Usando a definição, verifique se as funções a seguir são deriváveis em a e, em caso afirmativo, determine
f ′ (a).
(a) f (x ) = 2x − 3, a = 1 (b) f (x ) = 2x 2 − 5, a = −1(c) f (x ) =
√
x − 1, a = 1 (d) f (x ) = x 2 · |x | − 1, a = 0
3. Em que ponto da curva y = x 2 + 8 a inclinação da tangente é 16? Escreva a equação dessa reta
tangente.
4. Encontre a equação da reta tangente ao gráfico da função dada no ponto indicado.
(a) f (x ) = 2x 2 − 7 em (2, 1)
(b) f (x ) =
x2 − 1
em (1, 0)
x2 + 1
5. Encontre a derivada de cada uma das funções.
t 3 − 3t 2
(t − 2t )
t 5 − 5t
x3
ex
(f) f (x ) = x + 3
e
x
(g) f (x ) = x 2 sen(x ) − ln(x ) cos(x )
(e) f (t ) =
(a) f (x ) = 2x 4 − 3x 2 + 5x − 2
√
3
2
5
(b) f (x ) =
+ 2x ( x 3 ) − √
2x
x
(c) f (x ) = (3x 5 − 1)(2 − x 4 )
√
(d) f (s ) = 3(s 3 − s 2 )
(h) f (θ) = 2
cotg(θ)
1 − sen(θ)
6. Se f (x ) = e x · g (x ), em que g (0) = 2 e g ′ (0) = 5. É correto dizer que f ′ (0) é:
(a) 7
(b) 2
(c) 5
(d) 10
Derivada da Função Composta
7. Calcule a derivada de:
(a) y =
√
3
3x − 1
(d) f (t ) = ln(sec(x ))
(b) z (x ) = ln(x 2 − 6)
(c) f (t ) = e 4t
3
(e) y = cos[tg(3 − 5x )]
(f) y = sen(x 2 − 2x )
4t 3
(g) f (t ) = e t +4
√
(h) y = −3 − 7x cos(−15x )
”
€√4
√ Š—
(i) y = sec log2
x3 − 2
8. Encontre a derivadas das funções dadas.
(a) f (x ) = (3x 5 − 1)10 (2 − x 4 )
(g) f (θ) = 2 cos2 (θ) sen(θ)
(b) f (t ) =
(h) f (θ) = sen2 (θ) + cos2 (θ)

‹
x +1
(i) f (x ) = ln
ex
(j) f (x ) = ln(sen2 (x ))
3
3
(t − 3t )
(t 5 − 5t )5
(c) f (s ) = ln(e 5s −3 )
1
(d) f (x ) = ln(7x 2 − 4)
2
2
(e) f (x ) = e x + 4
(f) f (θ) = 2 cos(2θ2 − 3θ + 1)
L ISTA DE E XERCÍCIOS C ALC 1 #
(k) f (x ) = arctg(x 2 + 1)
(l) f (θ) = e arcsen(θ)
C ÁLCULO D IFERENCIAL E I NTEGRAL I
3
http://aluloifbaonquista.webnode.om.br
L’Hospital, Derivação Implícita, Diferencial e Taxas de Variação
9. Calcule o limite utilizando as regras de L’Hospital.
x
x →0 tg(x )
(a) lim
x
e − cos(x )
x →0 x sen(x )
(b) lim
10. Ache

ln(x )
√
x →+∞
x
(e) lim
x 2 + 6x
3
x →0 x + 7x 2 + 5x
(f) lim
(c) lim
x →+∞
ln
x
x +1
‹
x 99
x →+∞ e x
(d) lim
∂y
por derivação implícita:
∂x
(a) x 2 + y 2 = 16
1
1
(b) + = 1
x
y
(c) y 2 = cos(x − y )
(d) e x +y = arctg(y )
11. Calcular a derivada das seguintes funções:
(a) y = (2x 2 + x + 1)e x
2
(b) y =
È
ln[tg(3x )]
(c) y = 2sen(x )
(d)
x +1
ex
Crescimento, Extremante, Inflexão e Esboço de Gráficos
12. Verifique se estão satisfeitas as hipóteses do Teorema de Rolle para as funções a seguir, nos intervalos
especificados. Ache, então, um valor de c em cada um desses intervalos para os quais f ′ (c ) = 0.
•
˜
•
˜
•
˜
3
3
3 3
e I3 = − , .
(a) f (x ) = 4x 3 − 9x , I1 = − , 0 , I2 = 0,
2
2
2 2
¨
(b) f (x ) =
x +2 ,
4−x ,
x ≤2
e I = [−2, 4]
x >1
13. Verifique se estão satisfeitas as hipóteses do Teorema de Lagrange para as funções a seguir, nos
intervalos I especificados. Em seguida, obtenha um c ∈ I que satisfaça a tese do teorema.
(a) f (x ) = x 2 + 2x − 1 e I = [0, 1];
√
3
(b) f (x ) = x 2 e I = [0, 2];
(c) f (x ) =
x 2 + 4x
e I = [2, 6]
x −1
L ISTA DE E XERCÍCIOS C ALC 1 #
C ÁLCULO D IFERENCIAL E I NTEGRAL I
4
http://aluloifbaonquista.webnode.om.br
Gabarito
1. (a) f ′ (x ) = 2x , f ′ (0) = 0 e f ′ (1) = 2; (b) f ′ (x ) = 2x − 3, f ′ (−1) = −5 e f ′ (2) = 1; (c) f ′ (x ) = −
f ′ (x ) = cos(x ), f ′ (0) = 1, f ′
€πŠ
2
1
, f′
x2
€1Š
3
= −9 e f ′ (3) = −1/9; (d)
= 0 e f ′ (π) = −1. 2. 3. (8, 72) e y = 16x − 56. 4. (a) y = 8x − 15; (b) y = x − 1. 5. (a) 8x 3 − 6x + 5
√
1
2t 8 + 6t 7 − 18t 6 − 20t 5 + 30t 4 + 30t 3 − 30t 2
−x 3 + 3x 2
+ √ (c) −12x 8 − 15x 5 + 4x 3 + 30x (d) 3(3s 2 − 2s ) (e)
(f)
+
(t 5 − 5t )2
ex
x
3
cotg(θ)
1
1
− 4 (g) 2x sen(x ) + x 2 cos(x ) − + tg(x ) (h)
[2 − 2 cossec(θ) + cos(θ)] 6. 7. 8. (a) (3x 5 − 1)9 (−162x 8 + 300x 4 + 4x 3 );
ex
x3
x
x
[1 − sen(θ)]2
3
2
7
5
3
(t − 3t )(9t − 9t − 95t + 15t )
7x
2
(b)
; (c) 5; (d)
; (e) 2xe x ; (f) − sen(2θ 2 − 3θ + 1)(4θ − 3); (g) 2 cos2 (θ) cos(θ) − 4θ sen2 (θ) sen(θ);
(t 5 − 5t )6
7x 2 − 8
y 2
1
2x
e arcsen(θ)
(h) 0; (i)
. 9. (a) 1; (b) +∞; (c) 0; (d) 0; (e) 0; (f) 0. 10. (a) − xy ; (b) −
− 1; (j) 2 cotg(x ); (k) 4
; (l)
; (c)
2
x +1
x + 2x + 2
x
1 − θ2
(b)
−3
2x 2
€
+
√
16 5 3
x
5
Š
€ Š
p
(1 + y 2 )e x +y
2
3 sec 3x cossec 3x
sen(x − y )
; (d)
. 11. (a) dy = (4x 3 + 2x 2 + 6x + 1)e x dx ; (b) dy =
dx ; (c) ln(2) · 2sen(x ) · cos(x )dx ;
2y + sen(x − y )
e x +y − 1
2 ln[tg(3x )]
x
(d) dy = − x dx 12. 13.
e
p
−
L ISTA DE E XERCÍCIOS C ALC 1 #
C ÁLCULO D IFERENCIAL E I NTEGRAL I
5