CÁLCULO I 1 De nição

CÁLCULO I
Prof. Edilson Neri Júnior | Prof. André Almeida
Aula n
o
23: A Função Exponencial Natural
Objetivos da Aula
• Denir a função f (x) = ex ;
• Calcular limites, derivadas e integral envolvendo a função logarítmica f (x) = ex .
1 Denição
Na Aula 22, apresentamos a Função Logarítmica Natural. Vimos que esta função é crescente e, portanto,
injetora. Desta forma, a função f (x) = ln(x) possui uma função inversa, o qual denotaremos por exp.
Assim:
exp(x) = y ⇐⇒ ln(y) = x.
(1)
Note que, pelas propriedades de função composta, temos:
exp(ln(x)) = x e ln(exp(x)) = x.
(2)
Ainda, em particular temos:
exp(0) = 1 já que ln(1) = 0
exp(1) = e já que ln(e) = 1
Observação 1.
Se r for qualquer número racional, então a propriedade do logaritmo da potência nos dá:
ln(er ) = r ln(e) = r.
Portanto, pela equação 2:
exp(r) = er .
Logo, exp(x) = ex sempre que x for um número racional. Isso nos leva a denir ex , mesmo para valores
irracionais de x, pela equação
ex = exp(x)
Em outras palavras, denimos ex como a função inversa de ln x:
ex = y ⇐⇒ ln y = x.
(3)
Pelas propriedades de função composta:
e
eln x = x x > 0
(4)
ln(ex ) = x ∀ x.
(5)
1
Cálculo I
Aula n
o
23
1.1 Propriedades dos Expoentes
Teorema 1.
1.
ex+y
Se x e y forem números naturais e r for um número racional, então
= ex .ey
2. ex−y =
ex
ey
3. (ex )y = exy
Demonstração:
De fato, note que:
ln(ey .ey ) = ln(ex ) + ln(ey ) = x + y = ln(ex+y )
Como a função logarítmica natural é injetora, segue que ex .ey = ex+y . Analogamente,
(
ln
ex
ey
)
= ln(ex ) − ln(ey ) = x − y = ln(ex−y )
ex
. Finalmente, temos:
ey
ln(exy ) = xy. ln(e) = xy = y. ln(ex ) = ln((ex )y ).
Como a função logarítmica natural é injetora, segue que ex−y =
Como a função logarítmica natural é injetora, segue que (ex )y = exy .
1.2 Derivada de ex
Na Aula 11, mostramos que se uma função é derivável, então a sua inversa também será derivável.
Como y = ex é a inversa de y = ln x e esta é derivável (mostramos este fato na Aula 22), então a função
y = ex é derivável. Assim, utilizaremos o método da função inversa para calcular a derivada de y = ex .
Seja
y = ex =⇒ ln y = x
Derivando implicitamente a equação anterior, em relação a x, temos:
1 dy
.
=1
y dx
Logo:
dy
= y = ex .
dx
(6)
1.3 Gráco
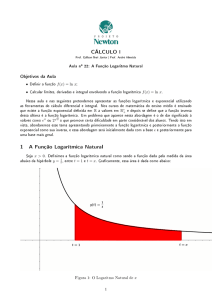
O gráco de y = ex é obtido reetindo-se o gráco de y = ln x em torno da reta y = x. O domínio
da função y = ex é a imagem de y = ln x, ou seja, (−∞, +∞) e a imagem de y = ex é o domínio de
y = ln x, ou seja, (0, ∞). Observe o gráco:
Prof. Edilson Neri | Prof. André Almeida
2
Cálculo I
Aula n
o
23
As propriedades da função exponencial natural decorrem do fato de que ela é a inversa da função
logarítmica natural. Como y = ex é uma função contínua crescente com domínio R e imagem (0, +∞),
para todo x ∈ R, temos que ex > 0. Temos também:
lim ex = 0 e
x→−∞
lim ex = +∞.
x→+∞
Logo, o eixo x é uma assíntota horizontal de y = ex .
Note que a primeira derivada da função y = ex é y ′ = ex > 0 para todo x. Ainda,
observe que a segunda derivada da função exponencial natural é y ′′ = ex > 0 para todo x. Logo, a função
exponencial natural é sempre crescente e côncava para cima.
Observação 2.
Observação 3.
Note que:
∫
ex dx = ex + C.
Alguns Exemplos
Exemplo 1.
Solução:
Calcule
d x2
(e ).
dx
Pela Regra da Cadeia, temos
d x2
2 d
2
(e ) = ex . (x2 ) = 2xex .
dx
dx
Exemplo 2.
Solução:
Calcule
d 2 x
(x e − xex ).
dx
Temos que:
d 2 x
d 2 x
d
(x e − xex ) =
(x e ) −
(xex )
dx
dx
dx
= 2xex + x2 ex − ex − xex
= x2 ex + xex − ex
= (x2 + x − 1)ex .
Exemplo 3.
Solução:
Calcule
d
(ln(ln x)).
dx
Pela Regra da Cadeia, temos:
d
1 1
1
(ln(ln x)) =
. =
.
dx
ln x x
x ln x
Exemplo 4.
valos de m?
Solução:
Uma reta cujo coeciente angular m passa pela origem é tangente a curva y = ln x. Qual o
Sabemos que:
• O ponto de tangência tem coordenadas (a, ln a).
• Nesse ponto, o coeciente angular da reta tangente é m =
Prof. Edilson Neri | Prof. André Almeida
1
.
a
3
Cálculo I
Aula n
o
23
Como a reta tangente passa pela origem, seu coeciente angular é:
m=
ln a − 0
ln a
=
a−0
a
Igualando as duas razões, temos:
ln a
1
=
a
a
ln a = 1
eln a = e1
a = e
Logo,
1
m= .
e
Exemplo 5.
Calcule
3(
∫
1
1+
x
1
Solução:
)
dx.
Temos que:
∫
3(
1
1+
x
1
)
∫
∫
3
dx =
1
=
3
1 dx +
[x]31
+ [ln
1
3
x]1
1
dx
x
= 2 + ln 3.
Exemplo 6.
Calcule
∫
1
e−x dx.
0
Solução:
Temos que:
∫
0
1
1
e−x dx = [−e−x ]10 = 1 − .
e
Exemplo 7.
Calcule:
∫
1
−1
Solução:
Temos que:
∫
1
−1
[
e
2x
e2x
dx =
2
e2x dx.
]1
=
−1
e2 e−2
e4 − 1
−
=
.
2
2
2e2
2 O Número e Expresso como um Limite
Na Aula 22, denimos e como o número tal que ln e = 1. Vamos demonstrar que:
e = lim (1 + x)1/x .
x→0
Prof. Edilson Neri | Prof. André Almeida
(7)
4
Cálculo I
Aula n
Seja f (x) = ln x. Então f ′ (x) =
23
1
, logo f ′ (1) = 1. Porém, pela denição de derivada:
x
f ′ (1) =
=
=
=
=
Como f ′ (1) = 1, temos:
o
f (1 + h) − f (1)
h
f (1 + x) − f (x)
lim
x→0
x
ln(1 + x) − ln 1
lim
x→0
x
1
lim ln(1 + x)
x→0 x
lim ln(1 + x)1/x
lim
h→0
x→0
lim ln(1 + x)1/x = 1
x→0
Pelo Teorema do Limite da Função Composta e pela continuidade da função exponencial, temos:
e = e1 = elimx→0 ln(1+x)
Exemplo 8.
1/x
x→0
Mostre que
lim
h→0
Solução:
1/x
= lim eln(1+x)
eh − 1
h
= lim ln(1 + x)1/x .
x→0
= 1.
Fazendo u = eh − 1, temos que h = ln(1 + u), temos que:
eh − 1
u
1
=
=
.
h
ln(1 + u)
ln(1 + u)1/u
Quando h → 0, temos que u → 0. Assim:
eh − 1
1
1
= lim
=
= 1.
u→0 ln(1 + u)1/u
h→0
h
ln e
lim
Resumo
Faça um resumo dos principais resultados vistos nesta aula, destacando as denições dadas.
Aprofundando o conteúdo
Leia mais sobre o conteúdo desta aula nas páginas A46 − A50 e no Apêndice G do livro texto.
Sugestão de exercícios
Resolva os exercícios da página A50 na seção de apêndices do livro texto.
Prof. Edilson Neri | Prof. André Almeida
5