Aula 22

CÁLCULO I
Prof. Edilson Neri Júnior | Prof. André Almeida
Aula no 22: A Função Logaritmo Natural
Objetivos da Aula
• Denir a função f (x) = ln x;
• Calcular limites, derivadas e integral envolvendo a função logarítmica f (x) = ln x.
Nessa aula e nas seguintes pretendemos apresentar as funções logarítmica e exponencial utilizando
as ferramentas do cálculo diferencial e integral. Nos cursos de matemática do ensino médio é ensinado
que existe a função exponencial denida em R a valores em R∗+ e depois se dene que a função inversa
dessa última é a função
√ logarítmica. Um problema que aparece nessa abordagem é o de dar signicado à
π
valores como e ou 2 2 o que promove certa diculdade em parte considerável dos alunos. Tendo isso em
vista, abordaremos esse tema apresentando primeiramente a função logarítmica e posteriormente a função
exponencial como sua inversa, e essa abordagem será inicialmente dada com a base e e posteriormente para
uma base mais geral.
1 A Função Logarítmica Natural
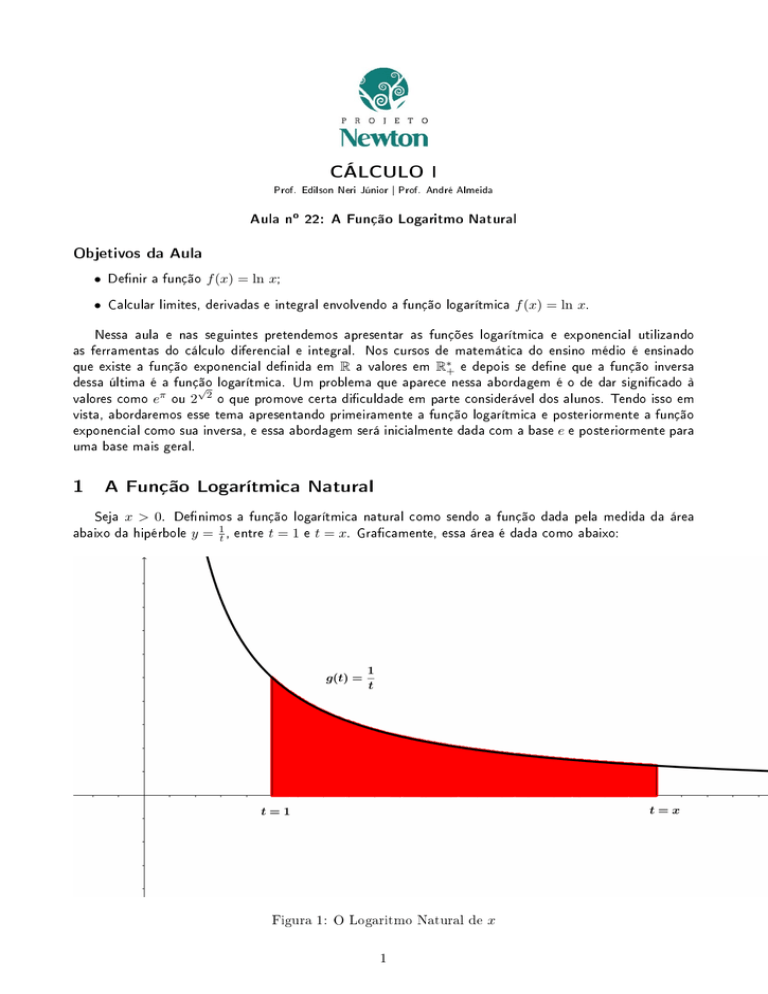
Seja x > 0. Denimos a função logarítmica natural como sendo a função dada pela medida da área
abaixo da hipérbole y = 1t , entre t = 1 e t = x. Gracamente, essa área é dada como abaixo:
Figura 1: O Logaritmo Natural de x
1
Cálculo I
Aula n
o
22
Como podemos entender a integral como a área abaixo de uma curva plana, então, podemos escrever
a denição de logaritmo natural como sendo:
x
Z
1
dt
t
f (x) = ln x =
1
(1)
Observação 1. Essa função está bem denida, pois a hipérbole existe em todos os pontos t = x, com
x > 0.
Observação 2. Note que se x > 0 então, a função f (x) > 0 e se 0 < x < 1 então f (x) < 0.
Denição 1. Denimos o número e como sendo o número tal que f (e) = ln e = 1.
2 Derivadas e Integral
Segue do Teorema Fundamental do Cálculo que para x > 0
f 0 (x) =
d
d
(ln x) =
dx
dx
Z
x
1
1
1
dt =
t
x
(2)
Considere agora a função g(x) = ln |x|. Note que g está denida para rodo x 6= 0. Mostraremos que
g 0 (x) =
1
.
x
Se considerarmos u = |x|, obtemos que g(u) = ln u e segue da regra da cadeia que
dg
dg du
1 du
=
=
dx
du dx
|x| dx
E observe que
|x| =
Logo,
d|x|
=
dx
Assim, podemos escrever
(3)
x se x > 0
−x se x < 0
1 se x > 0
−1 se x < 0
d|x|
|x|
=
, x 6= 0
dx
x
(4)
dg
1 |x|
1
=
=
dx
x
|x| x
(5)
Substituindo (4) em (3), temos que
O mesmo raciocínio obtido nesse último resultado pode ser aplicado para demonstrar a seguinte proposição
Proposição 1. Seja f uma função positiva. Então
d
f 0 (x)
(ln f (x)) =
dx
f (x)
(6)
Se f 6= 0, não necessariamente positiva, temos que
d
f 0 (x)
(ln |f (x)|) =
dx
f (x)
(7)
Devido a essa proposição, podemos concluir a seguinte armação:
Prof. Edilson Neri | Prof. André Almeida
2
Cálculo I
Aula n
Observação 3. Uma primitiva para f (x) =
o
22
1
é F (x) = ln |x| + C
x
Vejamos alguns exemplos:
Exemplo 1. Determine f 0 (x) sabendo que f (x) = ln sen2 x.
Solução: Note que a função f está denida para todo x ∈ R tal que x 6= nπ , n = 0, ±1, ±2, .... De
acordo com (6), temos que
df
(sen2 x)0
2sen x cos x
=
=
= 2cotg x
2
dx
sen x
sen2 x
Exemplo 2. Considere as seguintes funções
f (x) = ln
x+1
x−1
x + 1
g(x) = ln x − 1
Determine suas derivadas de primeira ordem e seus respectivos domínios.
Solução: Note que a função f está denida para x < −1 e x > 1, enquanto que a função g está denida
para x ∈ R − {−1, 1}. De acordo com (7), temos que
dg
=
dx
x+1 0
x − 1 (x + 1)0 (x − 1) − (x + 1)(x − 1)0
−2
(x
−1)
−2
x−1
=
=
= 2
x+1
2
x+1
(x − 1)2
x
−1
(x + 1)(x − 1)
x−1
(8)
dg
E note que
está denida para todo x ∈ R − {−1, 1}. Pela proposição (1), (8) é a derivada de f
dx
para x < −1 e x > 1.
Propriedades dos Logaritmos
Suponha a, b > 0. Considere as funções f (x) = ln x e g(x) = ln (ax). Observe que
g 0 (x) =
a
1
=
ax
x
Então, f 0 (x) = g 0 (x). Logo, pelo corolário do Teorema do Valor Médio, temos que
f (x) = g(x) + C
em que C é uma constante. Fazendo x = 1 na equação acima, obtemos que
ln a = ln 1 + C ⇒ C = ln a
Assim, podemos reescrever como
ln ax = ln x + ln a
Agora, substituindo x = b, obtemos que
ln ab = ln a + ln b
(9)
1
a
Fazendo b = , temos que
1
1
0 = ln 1 = ln a.
= ln a + ln
a
a
Assim,
Prof. Edilson Neri | Prof. André Almeida
3
Cálculo I
Aula n
ln
1
= − ln a
a
o
22
(10)
Dessa forma, temos que
ln
a
1
1
= ln a + ln = ln a − ln b
= ln a.
b
b
b
Logo,
ln
a
b
= ln a − ln b
(11)
E também que para
ln an = ln (a.a.a.a...a) = ln a + ln a + ... + ln a = n ln a
E, portanto,
ln an = n ln a
(12)
Utilizando a propriedade do quociente, podemos vericar que a propriedade acima é válida para todo
n ∈ Z.
Observação 4. Devemos tomar cuidado na aplicação da propriedade (12). Assim,
ln(x − 1)2 = 2 ln(x − 1)
é uma igualdade verdadeira apenas para x > 1. No entanto, como (x − 1)2 = |x − 1|2 , então podemos
fazer
ln(x − 1)2 = 2 ln |x − 1|
que é válida para todo x 6= 1. Portanto, é de extrema importância especicar o domínio quando utilizar as
propriedades para vericar a veracidade das igualdades obtidas.
Vejamos agora, alguns exemplos de como as propriedades podem nos ajudar no cálculo da derivada de
algumas funções.
√
Exemplo 3. Calcule a derivada da função f (x) = ln( x2 − 1 cos2 x).
Solução: Pela propriedade do logaritmo do produto, temos que
p
p
ln( x2 − 1 cos2 x) = ln( x2 − 1) + ln(cos2 x)
Pela proposição (1) e pela regra da cadeia, temos que
f 0 (x) =
x2
x
2 cos (−sen x)
x
+
= 2
− 2tg x
2
−1
cos x
x −1
em que o domínio de e f e f 0 é
n
o
π
Df 0 = x ∈ R; |x| > 1, x 6= kπ + , n ∈ Z
2
Exemplo 4. Seja g(x) = ln
x2 +1
x2 −1
Prof. Edilson Neri | Prof. André Almeida
. Calcule g 0 (x).
4
Cálculo I
Aula n
o
22
Solução: Utilizando a propriedade do logaritmo do quociente temos que
ln
x2 + 1
x2 − 1
= ln(x2 + 1) − ln(x2 − 1)
E, utilizando a proposição (1) a regra da cadeia, temos que
g 0 (x) =
3 − 2x
3 − 2x − 2x
2x
2x
2x
−4x
−
=
= 4
2
2
4
x +1 x −1
x −1
x −1
Exemplo 5. Utilize a derivada logarítmica para derivar a função
f (x) = x2 (x3 − 1)(x2 + 1)
Solução: Utilizando a regra do logaritmo do produto, temos que
ln |f (x)| = ln(|x2 ||x3 − 1||x2 + 1|) = ln |x2 | + ln |x3 − 1| + ln, kx2 + 1|
E utilizando a proposição (1), temos que
2x
3x2
2x
f 0 (x)
= 2 + 3
+ 2
f (x)
x
x −1 x +1
Logo,
2x
3x2
2x
f (x) = f (x)
+ 3
+
x2
x − 1 x2 + 1
3x2
2x
2x
2 3
2
+ 3
+
= x (x − 1)(x + 1)
x2
x − 1 x2 + 1
0
= 2x(x3 − 1)(x2 + 1) + 3x4 (x2 + 1) + 2x3 (x3 − 1)
= 7x6 + 5x4 − 4x3 − 2x
Exemplo 6. Utilize a derivada logarítmica para determinar a derivada da função
f (x) =
(x2 − 1)2 (x + 1)3
(x2 + 1)2
Solução: Utilizando a as propriedades de logaritmo temos que
2
(x − 1)2 (x + 1)3 ln |f (x)| = ln (x2 + 1)2
2
|x − 1|2 |x + 1|3
= ln
|x2 + 1|2
= ln |x2 − 1|2 |x + 1|3 − ln |x2 + 1|2
= ln |x2 − 1|2 + ln |x + 1|3 − ln |x2 + 1|2
= 2 ln |x2 − 1| + 3 ln |x + 1| − 2 ln |x2 + 1|
E segue da proposição (1) que
f 0 (x)
4x
3
4x
= 2
+
− 2
f (x)
x −1 x+1 x +1
o que implica que
3
4x
4x
f (x) = f (x)
+
−
x2 − 1 x + 1 x2 + 1
2
(x − 1)2 (x + 1)3
4x
3
4x
=
+
−
(x2 + 1)2
x2 − 1 x + 1 x2 + 1
4x(x2 − 1)(x + 1)3 3(x2 − 1)2 (x + 1)2 4x(x2 − 1)2 (x + 1)3
=
+
−
(x2 + 1)2
(x2 + 1)2
(x2 + 1)3
0
Prof. Edilson Neri | Prof. André Almeida
5
Cálculo I
Aula n
o
22
3 Gráco
Utilizando nossos conhecimentos sobre construção de grácos, vamos construir o gráco da função
f (x) = ln x. Para isso, note que Df = R∗+ . Observe também que se tomarmos x ∈ Df cada vez maior,
temos que f (x) assume valores positivos cada vez maiores. Sendo assim, podemos concluir que se x → +∞
então f (x) → +∞. Se x ∈ Df assume valores cada vez mais próximos de zero, a função f (x) assume
valores negativos cada vez menores, então concluímos que se x → 0+ então f (x) → −∞. E assim,
lim ln x = +∞
x→+∞
lim ln x = −∞
x→0+
1
> 0, logo, f é estritamente crescente. Note
x
< 0, portanto, f possui concavidade para baixo. Então como ln 1 = 0, então o
Notamos também que para x ∈ Df , temos que f 0 (x) =
também que f 00 (x) = − x12
gráco de f é dado por
Figura 2: Gráco da função f (x) = ln x
Para traçar o gráco de g(x) = ln |x|, basta notar que a função é par, pois
g(−x) = ln | − x| = ln |x| = g(x)
Agora, para x > 0, temos que
g(x) = ln |x| = ln x
Logo, o gráco desse subconjunto do domínio é igual ao da função ln x. E como a função é par, podemos
concluir que o gráco de g(x) = ln |x| é dado por:
Prof. Edilson Neri | Prof. André Almeida
6
Cálculo I
Aula n
o
22
Figura 3: Gráco da Função f (x) = ln |x|
Resumo
Faça um resumo dos principais resultados vistos nesta aula, destacando as denições dadas.
Aprofundando o conteúdo
Leia mais sobre o conteúdo desta aula nas páginas 196 − 200 e no Apêndice G do livro texto.
Sugestão de exercícios
Resolva os exercícios da página 201 e da página A50 na seção de apêndices do livro texto.
Prof. Edilson Neri | Prof. André Almeida
7