Revisão de Funções (Lista 1 e Lista 2)

Revisão de Funções (Lista 1 e Lista 2)
A noção de função via conjuntos
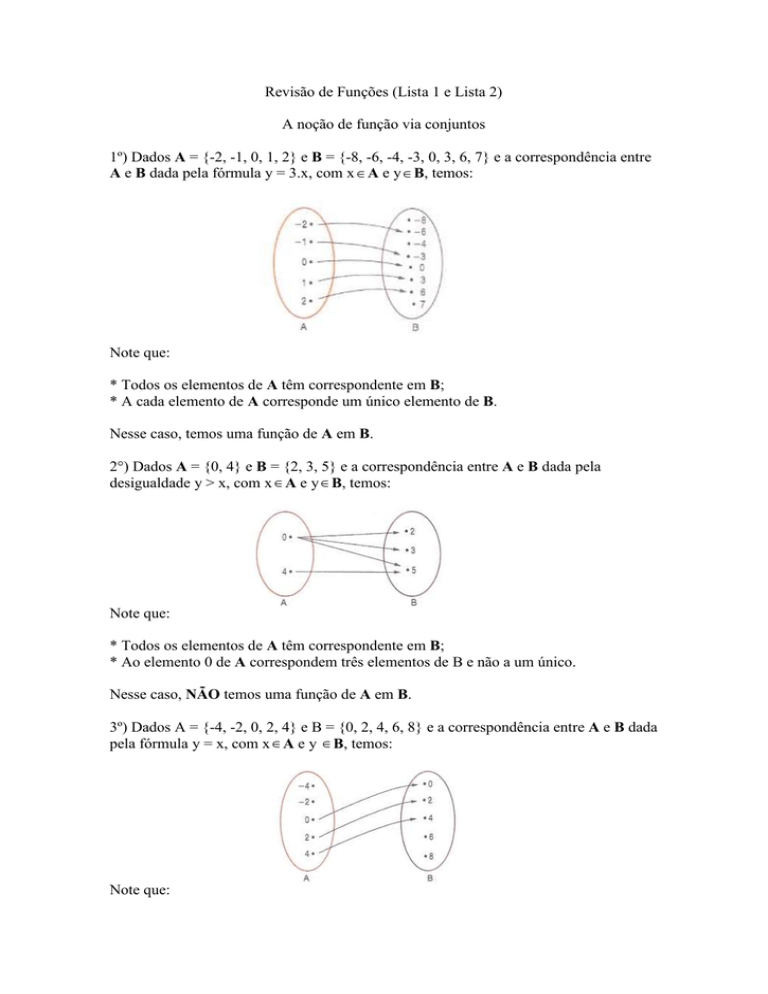
1º) Dados A = {-2, -1, 0, 1, 2} e B = {-8, -6, -4, -3, 0, 3, 6, 7} e a correspondência entre
A e B dada pela fórmula y = 3.x, com x  A e y  B, temos:
Note que:
* Todos os elementos de A têm correspondente em B;
* A cada elemento de A corresponde um único elemento de B.
Nesse caso, temos uma função de A em B.
2°) Dados A = {0, 4} e B = {2, 3, 5} e a correspondência entre A e B dada pela
desigualdade y > x, com x  A e y  B, temos:
Note que:
* Todos os elementos de A têm correspondente em B;
* Ao elemento 0 de A correspondem três elementos de B e não a um único.
Nesse caso, NÃO temos uma função de A em B.
3º) Dados A = {-4, -2, 0, 2, 4} e B = {0, 2, 4, 6, 8} e a correspondência entre A e B dada
pela fórmula y = x, com x  A e y  B, temos:
Note que:
* Há elementos de A (os números -4 e -2) que não têm correspondente em B.
Nesse caso, NÃO temos uma função de A em B.
4º) Dados A = {-2, -1, 0, 1, 2} e B = {0, 1, 4, 8, 16} e a correspondência entre A e B
dada pela fórmula y = x 4 , com x  A e y  B, temos:
Note que:
* Todos os elementos de A têm correspondente em B;
* A cada elemento de A corresponde um único elemento de B.
Nesse caso, temos uma função de A em B.
Definição e Notação
Dados dois conjuntos não-vazios A e B, uma função de A em B é uma regra que diz
como associar cada elemento x  A a um único elemento y  B.
Usamos a seguinte notação:
f: A  B ou
f
A 
B
que se lê: f é uma função de A em B.
A função f transforma x de A em y de B.
Exercícios Propostos
1) Quais dos seguintes diagramas representam uma função de A em B?
a)
b)
c)
d)
2) Dados A = {0, 1, 2, 3}, B = {-1, 0, 1} e a correspondência entre A e B dada por
y = x – 2, com x  A e y  B, faça um diagrama e diga se f é uma função de A em B.
Domínio, Contradomínio e Conjunto Imagem
1º) Dados os conjuntos A = {0, 1, 2, 3} e B = {0, 1, 2, 3, 4, 5, 6}, vamos considerar a
função f: A  B que transforma x  A em y B.
Em toda função f de A
em B, Im(f)  B.
Nesse caso, a função f: A  B está definida por y = 2.x ou por f(x) = 2.x.
Veja que para caracterizar uma função é necessário conhecer seus três componentes: o
domínio (A), o contradomínio (B) e uma regra que associa cada elemento de A a um
único elemento y = f(x) de B. Nesse exemplo, o domínio é A = {0, 1, 2, 3}, o
contradomínio é B = {0, 1, 2, 3, 4, 5, 6}, a regra é dada por y = 2.x e o conjunto imagem
é dado por Im(f): {0, 2, 4, 6}.
2º) Consideremos a função g:  definida por g(x) = x². Nesse caso a função g
transforma todo número inteiro x em outro número inteiro y que é o quadrado de x.
.
.
.
* A imagem de x = -2 é g(-2) = (-2)² = 4
* A imagem de x = -1 é g(-1) = (-1)² = 1
* A imagem de x = 0 é g(0) = (0)² = 0
* A imagem de x = 1 é g(1) = (1)² = 1
* A imagem de x = 2 é g(2) = (2)² = 4
.
.
.
Portanto, o domínio é , o contradomínio é , a regra é y = x² e o conjunto imagem é
, isto é, Im(g) = .
Generalizando:
Dada uma função h de A em B, o conjunto A chama-se domínio da função e o conjunto
B, contradomínio da função. Para cada x  A, o elemento y B chama-se imagem de x
pela função h ou o valor assumido pela função h para x  A e o representamos por h(x).
Assim, y = h(x).
O conjunto de todos os y assim obtidos é chamado conjunto imagem da função h e é
indicado por Im(h).
Exercícios Propostos
f
1) Considere a função A 
B dada pelo diagrama e determine:
a) D(f)
b) CD(f)
g) f(x), quando x = 5
c) Im(f)
d)f(4)
e) y, quando x = 6
f) x, quando y = 7
h) x, quando f(x) = 1
g
2) Considere A 
B a função para a qual A = {0, 1, 2, 3, 4} e B = {-2, -1, 0, 1, 4, 7,
10} e g(x) é o triplo de x diminuído de 2 para todo x  A.
a) Considere o diagrama de flechas da função:
b) Determine D(g), CD(g) e Im(g):
c) Determine g(3):
d) Determine x para o qual g(x) = -2:
Estudo do Domínio de uma Função Real
Vimos que uma função consta de três componentes: domínio, contradomínio e lei de
correspondência. Quando é citada uma função f de A em B, já ficam subentendidos o
domínio (A) e o contradomínio (B).
No entanto, às vezes é dada somente a lei da função f sem que A e B sejam citados.
Nesses casos consideramos o contradomínio B =
e o domínio A como o “maior”
subconjunto de (A
) tal que a lei dada defina uma função f: A  . Observe
os seguintes exemplos:
1º) f(x) =
2
x
Sabemos que o denominador de uma fração tem que ser diferente de zero, pois não
2
existe divisão por zero. Nesse caso, temos que ter x  0 para que
seja possível em
x
2
Para cada x  0, o valor
sempre existe e é único.
x
Logo, D(f) = - {0} = *.
2º) f(x) =
x4
Sabemos que no conjunto dos números reais ( ), não existe raiz quadrada de número
negativo.
Portanto, temos que ter x – 4  0 para que x  4 seja possível em .
x – 40  x  4
Para cada x  4, f(x) = x  4 existe e é único.
Logo, D(f) = {x 
x  4} = [4, + ∞[
3º) f(x) =
7x
x2
Nesse caso, devemos ter:
(I) 7 – x  0  -x  -7  x  7
e (II) x – 2 > 0  x > 2
.
Ou seja, x  ]2, 7]. Para cada x  ]2, 7], f(x) existe e é único.
Logo, D(f) = ]2, 7].
Exercícios Propostos
1) Explicite o domínio das funções reais definidas por:
x2
x ²  3x  2
4
d) f(x) = 3
x 1
a) f(x) = x² - 7x + 6
b) f(x) =
c) f(x) =
3
6 x
2
Construção de Gráficos de Funções
Para construir o gráfico de uma função dada por y = f(x), com x  D(f), no plano
cartesiano, devemos:
* Construir uma tabela com valores de x escolhidos convenientemente no domínio D e
com valores correspondentes para y = f(x);
* A cada par ordenado (x, y) da tabela associar um ponto do plano cartesiano;
* Marcar um número suficiente de pontos, até que seja possível esboçar o gráfico da
função.
Exemplos:
1º) Vamos construir o gráfico da função f:
Como, neste caso, D =

dada por f(x) = 2x + 1.
, vamos escolher alguns valores arbitrários de x:
x
-2
-1
0
1
2
y = f(x) = 2x + 1
-3
-1
1
3
5
O gráfico da função dada é o conjunto de todos os pontos (x, y), com x real e y = 2x + 1,
resultando na reta da figura abaixo.
2º) Vamos construir o gráfico da função
x
-2
-1,5
-1
0
1
1,5
2
Y = f(x) = -x²
-4
-2,25
-1
0
-1
-2,25
-4
f

dada por f(x) = -x².
(x, y)
(-2, -4)
(-1,5; -2,25)
(-1, -1)
(0, 0)
(1, -1)
(1,5; -2,25)
(2, -4)
A curva que contém todos os pontos obtidos com y = -x² é o gráfico da função dada.
Essa curva se chama parábola.
f
3º) Vamos construir o gráfico das função 
dada por f(x) =
Nesse caso, a função está definida por duas sentenças:
x
-1
1
3
x3
y = f(x) = x
-1
1
3
(x, y)
(-1, -1)
(1, 1)
(3, 3)
x, se x  3
3, se x > 3
f(x) = x, se x  3
f(x) = 3, se x > 3
x
4
5
6
x>3
y = f(x) = x
3
3
3
(x, y)
(4, 3)
(5, 3)
(6, 3)
Exercícios Propostos
1) Construa o gráfico de cada uma das seguintes funções y = f(x), f:

:
a) y = 2x + 3
b) f(x) = x² + 3
c) f(x) =
4x, se x  0
0, se x < 0
Como determinar o domínio e a imagem de uma função a partir do seu gráfico?
Observando o gráfico de uma função no plano cartesiano podemos, às vezes, determinar
o domínio D e o conjunto Im da função, projetando o gráfico nos eixos:
D(f) = { x 
Im(f) = {x 
2  x  4} = [2, 4]
D(f) = { x 
2  x  4} = [2, 4]
1  x  5} = [1, 5]
Im(f) = {x 
Exercícios Propostos
1  x  5} = [1, 5]
1) Os seguintes gráficos representam funções; determine o domínio D e o conjunto
imagem Im de cada uma delas:
a)
b)
c)
Determinando se um conjunto de pontos é gráfico de uma função
Já vimos que, para ter uma função de A em B, a cada x  A deve corresponder um único
y  B. Geometricamente, isso significa que qualquer reta perpendicular ao eixo x que
intersecta o gráfico deve fazê-lo uma única vez. Assim, se essa reta intersectar o gráfico
em mais de um ponto, esse gráfico não é gráfico de uma função. Por exemplo:
O gráfico acima é de uma função.
O gráfico acima não é de uma função.
Exercícios Propostos
1) Determine se cada um dos gráficos abaixo representa uma função:
a)
b)
c)
d)
Analisando o gráfico de uma função
De modo geral, analisando o gráfico de uma função, podemos observar propriedades
importantes dela, tais como:
1º) Onde ela é positiva (f(x) > 0), onde ela é negativa (f(x) < 0) e onde ela se anula
(f(x) = 0). Os valores x 0 nos quais ela se anula (f(x 0 ) = 0) são chamados zeros ou raízes
da função f.
2º) Onde ela é crescente (se x 1 < x 2 , então f(x 1 ) < f(x 2 )), onde ela é decrescente
(se x 1 < x 2 , então f(x 1 ) > f(x 2 )), onde ela é constante (se x 1 < x 2 , então f(x 1 ) = f(x 2 )) e
onde ela assume um valor máximo ou um valor mínimo, se existirem.
Exemplo:
Considere o gráfico abaixo de uma função definida no intervalo ]-6, 6[:
* f é positiva em ]-5, -1[ e em ]5, 6[.
* f é negativa em ]-6, -5[ e em ]-1, 5[.
* f é nula em x = -5, x = -1 e x = 5. Esses são os zeros ou raízes da função.
* f é crescente em ]-6, -3] e em [2, 6].
* f é decrescente em [-3, 2].
* O ponto com x = -3 é um ponto de máximo e f(x) = 2 é o valor máximo de f.
* O ponto com x = 2 é um ponto de mínimo e f(x) = -3 é o valor mínimo de f.
Exercícios Propostos
1) Considerando o gráfico a seguir, que representa uma função, responda:
a) Qual o domínio e a imagem da função?
b) Em que intervalos a função é crescente?
c) Em que intervalo a função é decrescente?
d) f (1) é maior, menor ou igual a f(4)?
f (5)
e) Qual o valor de
?
f (3)  f (2)
f) Quais são os zeros ou raízes da função?
g) Qual é o valor mínimo de f ?