Funções Polinomiais Funções Polinomiais 1ª Parte

Escola Básica e Secundária Dr. Ângelo Augusto da Silva
Matemática B – 11º Ano
ACTIVIDADE INVESTIGATIVA
Tema: Movimentos não lineares. Taxa de variação e funções racionais
Nome:______________________________ Turma: ___ Data: __/___/___
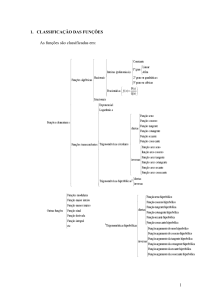
Funções Polinomiais
Objectivo:
Nesta actividade vai investigar a influência de vários parâmetros no comportamento de
funções polinomiais, nomeadamente a função afim, a função quadrática e a função
cúbica.
Material:
Calculadora gráfica TEXAS TI-83 ou TI-84
1ª Parte
Visualize os gráficos, recorrendo à calculadora gráfica, das funções definidas por
expressões do tipo f ( x ) = ax . Para tal, comece por atribuir a a diferentes valores, como
por exemplo a = 2; a = −2; a = 6. Registe os gráficos obtidos identificando a respectiva
função.
Faça agora um estudo semelhante para funções definidas por expressões do tipo
f ( x ) = 2 x + b , com b ∈ » . Dê valores distintos a b tal como na questão anterior.
1
Desenhe o gráfico indicando a respectiva função.
Analisando…
Características das funções do tipo y = ax + b com a, b ∈ » :
O gráfico da função é sempre uma __________
O domínio é ________
A constante b indica o ponto de intersecção com o eixo dos _____ (basta
observar que, em qualquer função deste tipo, a imagem de zero é _____).
O valor de ____ tem influência na monotonia, no sinal, no contradomínio e na
existência de zeros da função.
Quando a > 0 , a função é crescente e tem ____zero. À esquerda do zero a
função é _____________ e à sua direita é ___________.
Quando a ____ 0 , a função é decrescente e tem ____zero. À esquerda do zero
a função é _____________ e à sua direita é ____________.
Quando a ___ 0 , a função é _____________, não tem ________ (a não ser que
b = 0 ; neste caso tem uma infinidade de zeros). O seu contradomínio é______.
… A estas funções denomina-se por: Funções Afim
2ª Parte
Considere, agora as funções polinomiais de 2º grau, definidas por expressões do
tipo
f ( x ) = ax 2 + bx + c com a, b, c ∈ » e a ≠ 0 (ou
2
f ( x ) = a ( x − h ) + k com a ≠ 0 )
Represente as seguintes funções utilizando a calculadora gráfica:
2
1.
f ( x ) = 2x2
g ( x ) = −4 x 2
2.
f ( x ) = 2 ( x − 4 ) +1
;
2
;
;
h ( x) =
2
1 2
x
2
g ( x ) = −2 ( x − 4 ) − 1 ;
2
h ( x ) = ( x + 2) + 1
Analisando…
Características das funções do tipo f ( x ) = a ( x − h )2 + k com a ≠ 0 :
O gráfico da função é sempre uma __________.
O domínio é _____________.
O ponto de coordenadas ( h, k ) representa o___________.
O eixo de simetria é dado pela recta de equação ___________.
A concavidade é voltada para cima se ________ e é voltada para baixo se ________.
… A estas funções denomina-se por: Funções Quadráticas
3
3ªª Parte
Considere as seguintes funções polinomiais de 3º grau, definidas por expressões
do tipo f ( x ) = ax3 + bx 2 + cx + d com a, b, c, d ∈ » e a ≠ 0 .
g ( x ) = − x3 + 3x
h ( x ) = x3 − 3x 2 + 4
t ( x ) = 2 x3
Analisando os gráficos das funções representadas:
representadas
a) O que pode concluir acerca do domínio de cada uma das funções?________________
funções?________________
b) O contradomínio das
da funções
ões é: ____________________________________________
c) Indique um intervalo onde a função g ( x ) é decrescente_________________________
decrescente_________________________
d) No intervalo ]−∞, 0[ a função h ( x ) é ________________________________________
e) Indique os zeros de cada uma das funções ____________________________________
___________________________________
______________________________________________________________________
_______________________________________________________________________
Podemos dizer que…
Uma função cúbica tem pelo menos ___ zero e no máximo ____zeros
zeros
4