Ficha 2

Universidade da Beira Interior
Laboratório de Auto Regulação da Aprendizagem da Matemática
Curso: Sociologia
Ficha 1
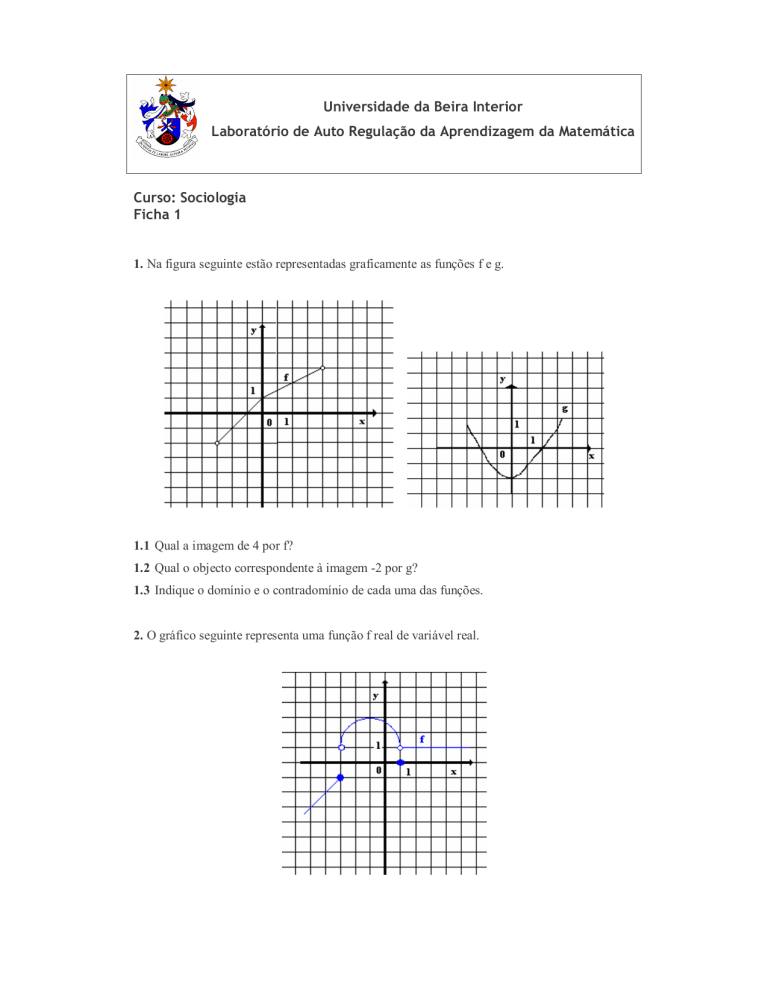
1. Na figura seguinte estão representadas graficamente as funções f e g.
1.1 Qual a imagem de 4 por f?
1.2 Qual o objecto correspondente à imagem -2 por g?
1.3 Indique o domínio e o contradomínio de cada uma das funções.
2. O gráfico seguinte representa uma função f real de variável real.
2.1 Indique o domínio e o contradomínio da função.
2.2 Complete a seguinte tabela:
x
-4
y = f (x)
-3
3
2
-3
4
0
2.3 Calcule o valor de :
a) f ( 3 ) − f ( −4 )
b) f (1) × f ( 4 )
3. Considere a função g, real de variável real, definida pela expressão g ( x ) = x 2 + 1 .
Determine:
3.1 As imagens dos objectos 2 e -3.
3.2 Os objectos cujas imagens são 3 e 1, respectivamente.
4. Sendo f ( x ) = −3x − 1 uma função real de variável real, determine os zeros e os intervalos em
que é positiva e negativa.
5. Considere a função f definida pelo gráfico seguinte:
Estude a variação da função f.
6. Das seguintes funções, indique justificando as que são não injectivas.
7. Considere a função f representada graficamente:
Estude os extremos da função f..
8. O gráfico seguinte representa uma função h,
Indique:
8.1 O domínio e o contradomínio da função.
8.2 Os zeros da função.
8.3 Os extremos relativos da função.
8.4 Os objectos cuja imagem é 1.
9. Considere, em IR, as funções f e g:
f ( x ) = 2x − 1 e
g ( x ) = − x 2 + 2x + 3
9.1 Determine f(0) e g(-2).
9.2 Calcule os valores de x, de modo que f(x) = 7.
9.3 Determine os zeros de g.
9.4 Determine o intervalo de
em que f é injectiva.
9.5 Calcule os valores de x, de tal modo que f(x) =g(x).
9.6 A função g é não injectiva. Justifique.
10. Relativamente à função f ( x ) = 2x 2 + 3 , definida em IR, justifique cada uma das seguintes
afirmações:
10.1 A função não tem zeros.
10.2 A função é sempre positiva.
10.3 A função não é injectiva.
11. À temperatura de 0ºC, o volume V que ocupa um gás ideal está relacionado com a pressão
P, do seguinte modo:
V=
22,4
P
(V em dm3 e P em atm)
11.1 Qual a pressão do gás quando ocupa um volume de 80 dm3 .
11.2 Desenhe e interprete o gráfico que corresponde à relação dada.
12. Considere a sequência:
12.1 Mantendo a regularidade, quantos pontos terá a próxima figura?
12.2 Considerando o número de pontos das figuras obtém-se os termos de uma sucessão.
Escreva uma expressão do termo geral desta sucessão.
12.3 A sucessão é crescente. Justifique.
13. Uma cultura de bactérias duplica de hora a hora. No inicio havia 30 bactérias.
13.1 Determine o número de bactérias ao fim de 1h, 2h e 3h.
13.2 Escreva uma expressão que permite calcular o número de bactérias existentes ao fim de n
horas.
14. O Vítor tinha um cofre onde guardava 500 euros e resolveu colocar todos os meses 50 euros
no cofre.
14.1 Se t é o dinheiro existente no cofre ao fim de n meses, escreva t em função de n.
14.2 Ao fim de quantos meses o Vítor terá 5 mil euros no cofre?
15. O número de indivíduos de um população é dada pela fórmula:
P = 100 ×1,5n
Sendo P o número de indivíduos e n o número de anos decorridos.
15.1 Determine o número de indivíduos ao fim de 5 anos.
15.2 Determine, ao fim de 10 anos, o número de indivíduos da população.
16. O QI (quociente de inteligência) é determinado pela razão entre a idade mental (IM),
calculada através de testes estandardizados e a idade cronológica (IC) e multiplicando o valor
obtido por 100.
16.1 Se uma menina de 8 anos tem um QI de 125, qual é a sua idade mental?
16.2 Se um rapaz tem idade mental de 15 e um QI de 120, qual é a sua idade cronológica?
16.3
Fixando o valor de 120 para o QI, represente graficamente a relação entre a idade
cronológica e a idade mental.