POTÊNCIA EM CARGAS GENÉRICAS

POTÊNCIA EM CARGAS GENÉRICAS
Prof. Antonio Sergio C. de Menezes. Depto de Engenharia Elétrica
Muitas cargas numa instalação elétrica se comportam de forma resistiva ou
muito aproximadamente como tal. Exemplo: lâmpadas incandescentes comuns
(lâmpada de Edson), chuveiros elétricos, todos os tipos de aquecedores como fornos
elétricos, por exemplo. A questão é que as cargas não são sempre do tipo resistivas. Há
também as chamadas cargas reativas, como motores em geral como ventiladores,
geladeiras, ar-condicionados, e outras como lâmpadas fluoerescentes, transformadores
(cada aparelho eletrônico ligado à tomada tem um transformador de entrada), sem
contar com um ambiente industrial que tem normalmente muitas máquinas elétricas.
Vamos admitir que excitamos uma carga qualquer com uma tensão senoidal
(um ventilador, por exemplo, ou uma lâmpada ou conjunto de lâmpadas fluoerescentes).
Vamos admitir também que esta carga responde à excitação senoidal de voltagem com
uma corrente igualmente senoidal. Chama-se isso de resposta linear. A retificação de
meia-onda mostrada é um exemplo de resposta não-linear.
De maneira geral, se v(t) = Vm.sen(ω.t) é a tensão aplicada a uma carga
reativa, esta responde com uma corrente atrasada ou adiantada de i(t) = Im .sen(ω.t +/φ). Assim, a potência instantânea fornecida pela fonte (gerador) é dada por:
p(t) = Vm.Im. sen(ω.t). sen(ω.t- φ)
(1)
Aplicando a esta expressão a identidade
Assim, tem-se:
V .I
p(t) = m m [cos(φ) − cos(2ωt − φ)]
2
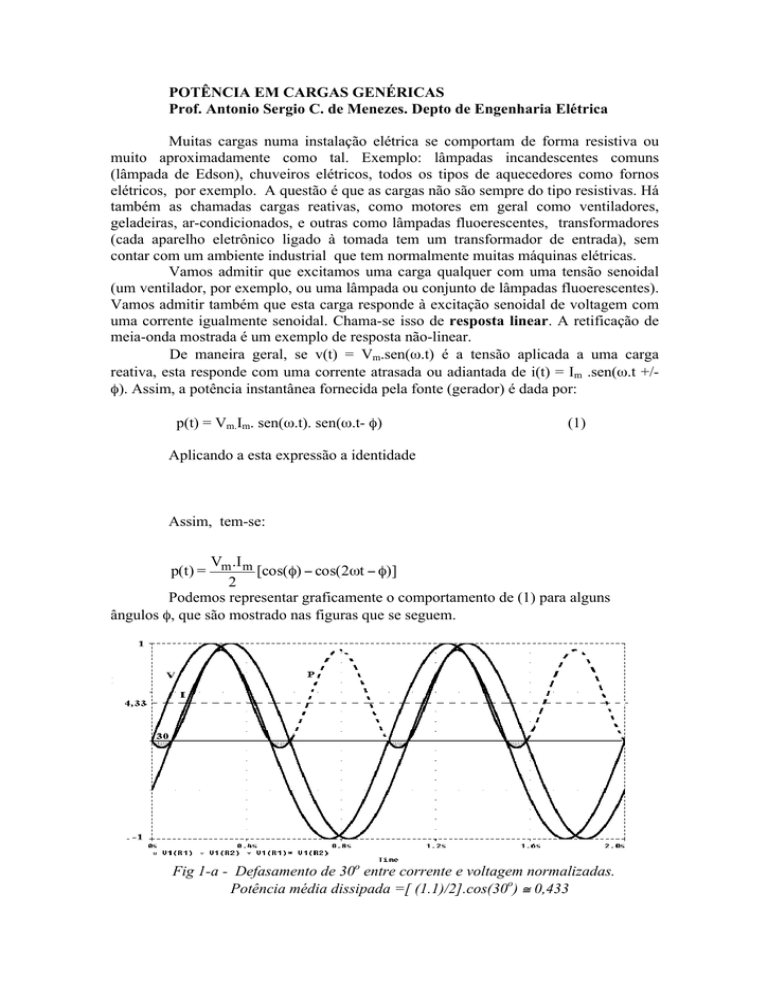
Podemos representar graficamente o comportamento de (1) para alguns
ângulos φ, que são mostrado nas figuras que se seguem.
Fig 1-a - Defasamento de 30o entre corrente e voltagem normalizadas.
Potência média dissipada =[ (1.1)/2].cos(30o) ≅ 0,433
Nota-se pelas figuras acima a potência desenvolvida numa carga reativa é de
natureza cíclica e tem uma frequência duas vezes maior que a frequência da corrente e
da voltagem. A parte do ciclo da potência que fica no semi plano positivo representa a
potência ativa, cuja média depende do defasamento: quanto maior o defasamento,
menor é a média. O semiciclo negativo representa a energia reativa não transformada e
devolvida à fonte-alimentador.
Para justificar isto matematicamente, tem-se que a potência média fornecida
pela fonte-gerador é dada por:
P=
1 Vm .I m
[cos(φ) − cos(2ωt − φ)].dt
T 2 ∫
Fig 2-b – Defasamento de 60o entre corrente e voltagem normalizados
Potência média dissipada = [(1x1)/2]x cos(600)
A integral acima tem duas parcelas: uma constante [cos(φ)] e outra dependente
do tempo [ cos(2ωt − φ) ] que, conforme a expressão (1) é zero, pois trata-se de uma
função senoidal.
Assim,
V .I
V I
P = m m .cos(φ) = m m cos(φ) = VRMS.I RMScos(φ)
2
2. 2
ou simplesmente
P=V.I.cos(φ)
(2)
pois subtende-se que V e I são os valores RMS, já que sempre estaremos tratando de
valores alternados de voltagem e de corrente. A expressão (1) representa a potência
efetivamente consumida pelo circuito, isto é, a parte da energia fornecida pela fontegerador transformada em outra forma de energia, desde que φ esteja compreendido
entre -90o e +90o. Fora deste intervalo P assumiria valores negativos o que significa que
o circuito estaria fornecendo energia à fonte que, para nossos propósitos, não será
considerado. cos(φ) é chamado fator de potência. É o fator que, multiplicado pela
potência aparente (VI), dá a energia elétrica efetivamente transformada em outra
forma de energia, ou trabalho realizado.
Apesar das potências médias desenvolvidas pelo indutor ou capacitor serem
nulas, há circulação de corrente pelos mesmos.
Exemplo 1:
Uma voltagem do tipo v(t) = 100.sen(ω.t + 30o) é aplicada a um certo circuito
que responde com uma corrente do tipo i(t) = 5.sen(ω.t -20o). Qual a potência
aparente fornecida ao circuito e qual a potência efetivamente desenvolvida pelo
mesmo?
Solução.
Os valores efetivos da voltagem e da corrente são:
V=
100
2
e
I=
5
2
O defasamento é φ = 30o – (-20o) = 50o . Assim, a potência fornecida é:
S=
100 5
x
= 250VA
2
2
S também chamada de potência aparente e tem unidade de Volt-Ampére.
Observe que os estabilizadores de voltagem usados em computadores e outros fins tem
suas potência expressas em VA, pois este são fornecedores de energia e de voltagem
alternada.
Quanto à potência efetivamente consumida, P, usa-se a Eq. 24:
P=
100 5
x
x cos(50o) = S x cos(50o) = 160,7 W
2
2
Z = 20 ∠50o = 12,86 + 15,32. Logo, R = 12,856 Ω.
2
⎛ 5 ⎞
P = R.I = 12,856x ⎜
⎟ = 160,7 W
⎝ 2 ⎠
2
1-1- Potência em cargas resistivas
Pela lei de Ohm, a corrente que circula por uma carga resistiva é dada por:
V
VDC
ou I RMS = RMS =
(3)
R
R
Ou ainda, supondo-se que o resistor é excitado por uma tensão senoidal:
IDC =
v(t) Vmsen(ω.t)
=
= I msen(ω.t )
R
R
Vê-se acima que o que diferencia v(t) de i(t) é um constante multiplicativa.
Logo, conclui-se que a corrente e voltagem estão fase, como pode ser observado pela
Fig. 2.
i(t) =
A potência instantânea dissipada pelo resistor R é dada por:
p(t) = v(t).i(t) = Vm.sen(ω.t)x Im.sen(ω.t).= Vm Im sen2(ω.t).
Determinando a potência média dissipada pelo resistor, tem-se:
T
T
0
0
1
1
P = ∫ v(t).i(t).dt = ∫ Vm .I m .sen 2 (ω.t).dt
T
T
Considerando a equação (17), tem-se:
V I
(4)
P = m m = V.I.cos(0o )
2
O que está de acordo com a expressão (2), dado que o defasamento entre
voltagem e corrente numa carga resistiva é 0o. Assim, o resistor dissipa toda a energia
fornecida pela fonte-gerador.
Há muitos exemplos de cargas resistivas em instalações elétricas: todos os
tipos de aquecedores elétricos passando aí por fornos, chuveiros, cadinhos, entre outros,
também lâmpadas incandescentes de filamento, as chamadas lâmpadas de Edson,
lâmpadas usadas em todo tipo de projetores, etc. As lâmpadas fluorescentes comuns e as
lâmpadas florescentes eletrônicas são cargas indutivas e, portanto, não tem
comportamento resistivo
Fig. 2 Comportamento da corrente em relação à voltagem à potência
em uma carga resistiva.
Observa-se pela figura acima que a potência é toda positiva, o que significa
toda a potência é dissipada e nada é devolvido.
2 – Potência em indutância.
Um circuito indutivo sempre tem uma resistência associada à ele, pois um
indutor é construído enrolando-se um fio de cobre esmaltado num núcleo de ar ou de
material magnetizável..Mas quando se pode desprezar esta resistência, diz-se que o
indutor é ideal.
Quando um indutor está submetido a um sinal senoidal, como é o nosso caso,
podemos considerá-lo ideal quando ωL >>R, onde ω é a frequência em radianos/seg do
sinal, L é o valor da indutância e R é valor da resistência associada. Uma das formas de
se conseguir isso é enrolar a espira do indutor com um fio de cobre de grande seção
com grande número de voltas sobre um núcleo ferromagnético.
A relação entre corrente e voltagem num indutor é dada por:
Admitindo-se que este indutor é excitado por uma corrente senoidal e
aplicando-se na expressão acima tem-se:
d
v(t) = L [I m .sen(ω.t)] = ωLI m .cos(ω.t) = ωLI m .sen(ω.t + 90 o )
dt
(5)
v(t). = Vmsen(ω.t + 90o ) ,
Isto é, o indutor reage contra variação da corrente adiantando a voltagem em
90o ou atrasando a corrente em 90o.
Vm = ωLI m
Fig 3 – Comportamento da corrente, da voltagem e da potência em um
indutor ideal.
Assim sendo, usando-se a Eq. (1) e integrando-a, temos que a potência média
desenvolvida pelo indutor ideal é dada por:
P = V.I.cos (90o) = 0
A expressão acima indica que o indutor ideal não dissipa energia. Em outras
palavras, o indutor ideal não transforma energia elétrica em outra forma de energia
como outras cargas, como lâmpadas e motores em geral, por exemplo. A energia circula
pelo indutor ideal de forma cíclica e simétrica em relação ao eixo dos tempos: em um
semi-ciclo a energia é armazenada no campo magnético do indutor e no outro semiciclo esta energia é devolvida para a fonte-alimentador. Mas esta circulação de energia
implica numa circulação de corrente que sobrecarrega desnecessariamente o
alimentador.
3 Potência em capacitor ideal.
Tecnicamente falando é muito fácil um capacitor se aproximar da idealidade do
que o indutor. A indústria sempre tem apresentado evoluções na construção deste
elemento.
Supondo-se mais vez que o capacitor é excitado por uma corrente senoidal ,
pode-se relacionar v(t) e i(t) num capacitor da seguinte forma:
1
1
I
I
i(t).dt = ∫ I m .sen(ω.t).dt = − m cos(ω.t) = − m sen(ω.t + 90 o )
∫
C
C
ωC
ωC
o
Considerando que –sen(x) = sen (x ± 180 ), tem-se:
I
(6)
Vm = m
v(t) = Vmsen(ω.t − 90o ) , onde
ωC
v(t) =
Num capacitor ideal a voltagem se atrasa de 90o em relação à corrente. E novamente, considerando-se a Eq. (1) e integrando-a, tem-se:
P = V.I.cos 0o
O que leva ao mesmo tipo de conclusão de dissipação de energia que se teve em
relação ao indutor ideal, isto é, o capacitor ideal também não converte energia elétrica
em outra forma de energia, e o que acontece em relação ao campo magnético do
indutor, acontece também em relação ao campo elétrico do capacitor.
Exemplo 2:
Ligou-se na mesma tomada uma carga resistiva de 200W e um motor de 1/3 de
HP, e fator de potência 0,7. Determinar a corrente total fornecida pela tomada? A
tomada fornece 220V/60Hz
Solução:
Para a carga resistiva, tem-se φ = 0o o que implica em cos(ϕ) = 1. Assim,
|I r | =
P 300
= 1,364A
=
V 220
Fasorialmente, tem-se: Ir = 1,364∠0o.
Para o motor, no entanto, tem-se:
|I v | =
P
746/3
=
= 1,615A
V.cos(φ) 220.0,7
Fasorialmente, tem-se: IV = 1,615∠-45,57o = 1,131 - j.1,153. A total da tomada é
dada por:
IT = Ir + IV = 1,364 + 1,131 - j.1,153 = 2,96 - j.1,154 = 2,75∠-24,81o
Um amperímetro colocado entre a saída da tomada e as duas cargas ler o módulo
de IT, ou seja, 2,75A . Observe que, se somarmos os módulos das correntes de cada
carga, obteremos 1,364 + 1,615 = 2,98 A. Um valor maior que o obtido pela soma
fasorial.
Em diagrama fasorial, tem-se (regra do paralelogramo):
Fig.4 - Diagrama fasorial do exemplo acima
Exemplo 3:
Um motor indutivo de 100W e fator de potência 0,6 é colocado em paralelo com
outro capacitivo de 150W e fator de potência 0,7. Ambos são ligados em 220V.
Calcular a corrente total do conjunto.
Solução:
Trata-se de um circuito RL em paralelo com um RC. Para isso, emprega-se a
expressão P = V.I.cos(θ).
O módulo da corrente do circuito indutivo é:
|I M1| =
P
100
=
= 0,758A
V.cos(φ) 220.0,6
A corrente fasorial dele é IM1 = 0,758∠-53.13o = 0,455 - j.0,606
O módulo da corrente do circuito capacitivo é:
|I M2|=
P
150
=
= 0,974 A
V.cos(φ) 220.0,7
A corrente fasorial dele é IM2 = 0,974∠+45,57o = 0,682+ j.0,696
Somando-se as duas correntes tem-se:
IMT = 1,137+j.0,09 = 1,141 ∠+4,5o
Note que o ângulo da corrente total foi praticamente nulo. É que a carga capacitiva
tende a anular a reatividade da carga indutiva. Logo, o circuito tem um comportamento
praticamente resistivo.
TRIÂNGULO DE POTÊNCIA
Vimos que P = V.I.cos(φ).
Aonde P é potência média consumida, V é o valor eficaz da tensão do alimentador – que
no caso do Nordeste Brasileiro é de 220V, I é a corrente eficaz que circula pelas cargas
e φ é o defasamento entre a esta corrente e aquela voltagem. O produto N = V. I ou S =
V.I é a potência aparente e cos(φ) é conhecido como sendo o fator de potência, isto
é, o fator que multiplicado pela potência aparente dá o quanto da potência entregue é
transformada (dissipada) em outra forma de energia (mecânica, luminosa, térmica, etc).
Exemplo 4:
Uma certa geladeira traz as seguintes informações acerca de seu consumo:
- Alimentação: 220V; consumo : 160W; corrente : 1,2A.
Logo, a potência aparente entregue a esta geladeira é:
N=V.I=220X1,2=264VA
O fator de potência é facilmente calculado como sendo:
cos(φφ=
P
= 0,606 → φ = cos−1 (0,606) = 52,70 0
N
Assim, como a geladeira tem um motor indutivo, a corrente fasorial dela é:
I G = 1,2∠ − 52,70 0 = 0,72–j0,955
Se quisermos a impedância equivalente complexa associada ao motor da geladeira
fazemos:
Z=
V
I
=
220∠00
1,2∠ − 52,70
0
= 183,33∠ + 52,70 0 = 111,10 + j.145,83
(7)
Observando acima, podemos perceber que N é hipotenusa de um triangulo retângulo e
P, seu cateto adjacente, só faltando, portanto, o cateto oposto deste triangulo e este
cateto oposto é a potência reativa Q do motor como poderia ser de uma instalação
monofásica qualquer. Assim, o triangulo abaixo representa graficamente a situação
acima
P
Q
N
Fig. 5 – Triangulo de potência para uma carga reativa.
Assim, temos as seguintes relações para as potências envolvidas numa carga reativa (e
mesmo não reativa)
P=N.cos(φ)
(8.1)
Q=N.sen(φ)
(8.2)
N2=P2+Q2
(8.3)
Sabe-se também que a potência ativa P é matematicamente justificada pela parte REAL
da impedância complexa. Também, dedui-se que a potência reativa Q é justificada pela
parte IMAGINÁRIA da mesma impedância. Assim, considerando que
, temse:
P = R.I2
(9.1)
Q = X.I2
(9.2)
Ainda em relação ao caso da geladeira acima, e considerando (2), (6.1) e (6.2), temos:
P = 264.cos(52,700) = 160W
(10.1)
Q= 264.sen (52,700) = 210 VAR
(10.2)
Por outro lado, considerando (7), (8.1) e (8.2), tem-se:
P = 111,10.(1,2)2 = 160W
(11.1)
2
Q = 145,83(1,2) = 210VAR
Assim sendo, o triangulo de potência para a geladeira acima é:
160W
210VA
264VA
Obs: o ângulo da impedância é o mesmo ângulo do triangulo de potência.
(11.2)
Exemplo 5
Solução:
Uma voltagem do tipo v(t) = 150.sen(ω.t + 10o) é aplicada a um certo circuito que
responde com uma corrente do tipo i(t) = 5.sen(ω.t -50o). Determinar o triângulo das
potências
Solução.
Os valores efetivos da voltagem e da corrente são:
V=
150
2
e
I=
5
2
O defasamento é φ = 10o – (-50o) = 60o . Assim, a potência aparente é:
S=
150 5
x
= 375VA
2
2
P = S. cos(60o) = 187,5W
e Q = S.sen(60o) = 324,76 VAR