Flexão

Flexão
Flexão
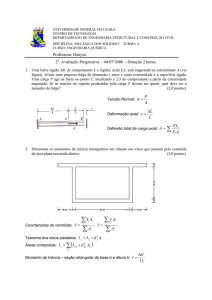
• Considere-se a viga simplesmente apoiada,
submetidas a duas forças concentradas, como
ilustra a Figura abaixo.
Flexão
• Essas forças produzem deslocamentos nos diversos
pontos do eixo da viga dando origem a tensões
internas. As fibras inferiores serão alongadas, ficando
sujeitas a esforços de tração e as fibras superiores
serão encurtadas, ficando sujeitas a esforços de
compressão.
Essas
deformações
originam
internamente na viga tensões de tração e de
compressão. Observa-se que a tensão σx é
proporcional à distância da Linha Neutra. As tensões
variam linearmente com a distância do eixo neutro.
Flexão
Flexão
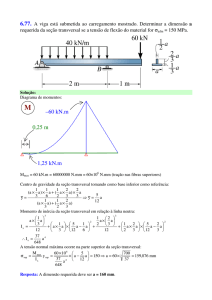
• Para o calculo da tensão de normal ao longo do
corpo do sólido teremos que utilizar a seguinte
equação:
•
•
•
•
Onde:
M = Momento fletor
I = Momento de Inercia
y = é a distância da LN até o ponto que se quer
calcular a tensão.
Momento de Inércia
• O momento de inércia mede a distribuição da
massa de um corpo em torno de um eixo de
rotação. Quanto maior for o momento de
inércia de um corpo, mais difícil será fazê-lo
girar. Contribui mais para a elevação do
momento de inércia a porção de massa que
está afastada do eixo de giro.
Tensão
Do estudo das características geométricas de
seções planas, define-se Módulo Resistente
(W) por:
Tensão
Então, temos que a tensão normal fica:
Momento de Inércia
Quando a viga tiver seção retangular, com
largura b e altura h, o Momento de Inércia e o
Módulo Resistente, são respectivamente:
Momento de Inércia
Para uma barra circular de diâmetro d,
tem-se: