sen(α)=cos(90-α) cos(α)=sen(90-α) sen(α)=sen(180-α

Prof. Gabriel Cremona Parma
=
X’
á
=
í
.
eixo dos senos
=
=
X’
=
á
í
eixo das tangentes
=
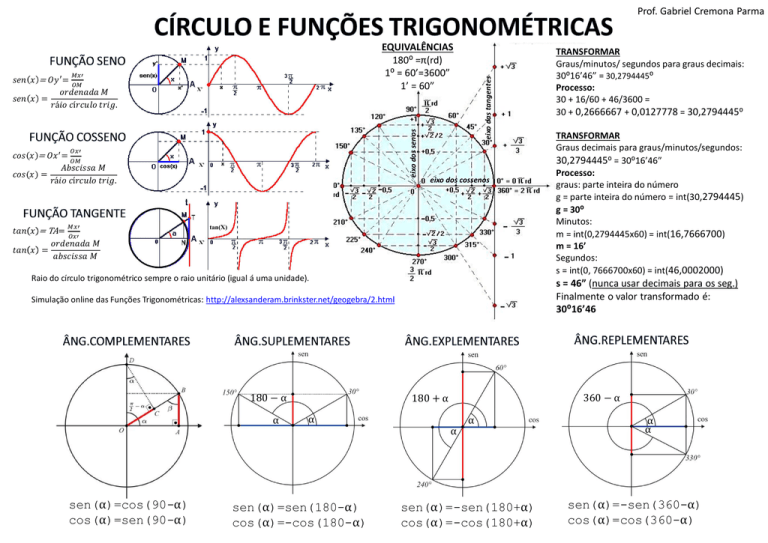
EQUIVALÊNCIAS
180⁰ =π(rd)
1⁰ = 60’=3600”
1’ = 60”
.
eixo dos cossenos
tan(X)
= TA=
X’
=
Raio do círculo trigonométrico sempre o raio unitário (igual á uma unidade).
α
360 − α
180 + α
α
α
α
sen(α)=cos(90-α)
cos(α)=sen(90-α)
sen(α)=sen(180-α)
cos(α)=-cos(180-α)
TRANSFORMAR
Graus decimais para graus/minutos/segundos:
30,2794445⁰ = 30⁰16’46”
Processo:
graus: parte inteira do número
g = parte inteira do número = int(30,2794445)
g = 30⁰
Minutos:
m = int(0,2794445x60) = int(16,7666700)
m = 16’
Segundos:
s = int(0, 7666700x60) = int(46,0002000)
s = 46” (nunca usar decimais para os seg.)
Finalmente o valor transformado é:
30⁰16’46
Simulação online das Funções Trigonométricas: http://alexsanderam.brinkster.net/geogebra/2.html
180 − α
TRANSFORMAR
Graus/minutos/ segundos para graus decimais:
30⁰16’46” = 30,2794445⁰
Processo:
30 + 16/60 + 46/3600 =
30 + 0,2666667 + 0,0127778 = 30,2794445⁰
sen(α)=-sen(180+α)
cos(α)=-cos(180+α)
α
α
sen(α)=-sen(360-α)
cos(α)=cos(360-α)
Prof. Gabriel Cremona Parma
A
      180 
se :   90  
    90 
α
b
Area  base  altura 2
raio circunf. inscrita  r
raio circunf. circunscrita  R
abc
s
2
( s  a )( s  b )( s  c )
r
s
γ
β
C
a
Funções Básicas
a cat .op .
sen  
 cos 
c
hip .
b cat .adj
cos   
 sen 
c
hip .
a cat .op .
tan   
 cot 
c cat .adj
b cat .adj
cot   
 tan 
a cat .op .
Teorema Pitágoras
Area  rs 
s ( s  a )( s  b )( s  c )
Area  2 R 2  sen  sen   sen
Area  a  b  sen 2
a2  c2  b2 ; b2  c2  a2
Relações Fundamentais
sen
1
tan  =
, cot  
cos 
tan 
 sen 
2
  cos    1
C
  90 
  90 
  90 
α
c
γ
a
β
B
Teorema Seno
a
b
c


 2R
sen sen sen
Teorema cosseno
a 2  c2  b 2  2  c  b  cos
b2  c2  a 2  2  c  a  cos 
c 2  a 2  b2  2  a  b  cos
tan

2

r

r

r
; tan 
; tan 
( s  a)
2 ( s  b)
2 ( s  c)
c2  a2  b2 
2
A
b
c
B
      180 
( s  b)( s  c )


; sen  ...; sen  ...
2
bc
2
2
a  sen
tan  
; tan   ...; tan   ...
c  a  cos 
sen


Teoerma Tangentes
 
tan
2  a  b ;     90  
   a b
2
2
tan
2
Teorema projeções
a  b  cos   c  cos 
b  a  cos   c  cos 
c  b  cos   a  cos 
Prof. Gabriel Cremona Parma
A
α
b
  90 
  90 
  90 
Caso 2: dois lados e o ângulo compreendido. Dados: a; b; γ
Método A:
=
=
c
Método B:
+
×
= 180° −
−2
×
+
2
=
−
a
β
a=
= 90 −
=
→
B
Calcular primeiro:
=
×
=
Solução básica
= 180° −
×
c=
Verificação da Solução:
c) Se:
×
= 180 −
= 180° − −
×
=
çã .
ℎ
çã ú
:
→verificar possível segunda solução
< →
çã :
= →
uma única
çã
<
−Se: ×
−Se: ×
−
Segunda Solução
a) Se : ×
> → ã
b) Se: ≥ → < 90°:
−
çã
:
= 90°
= 90° − ; c= ×
Caso 4: três lados. Dados: a; b; c
=
Método A:
Método B:
=
;
+ +
; =
2
=
Caso 3: 2 lados e o ângulo oposto. Dados: a; b; α (Caso duvidoso)
Caso 1: um lado e dois ângulos
adjacentes. Dados: c; α; β
= 180° −
×
b=
×
2
+ ; β=
×
c=
C γ       180 
=
=
;
= 180° −
( − )( − )( − )
;
−
=
−
;
=
−
; = 180° −
−
Prof. Gabriel Cremona Parma
ORIGEM ORIENTAÇAO NO EIXO HORIZONTAL +Y (NORTE)
=
é
;
;
;
;
çõ
=
=
=
/
−
−
−
.
(
)
ç
=
ℎ
=
â
ℎ
=
Â
çã
=
;
:
=
;
çã ℎ
=
Â
=
ℎ
=
=
+
:
; ;
:
ℎ
;
+
+
+
ℎ
;
=
:
;
=
ARREDONDAMENTO DE NÚMEROS
•
X
Medidas lineares com precisão de milímetros:
– Três casas decimais depois da vírgula. CERTO: 234,233m ERRADO: 234,233441214m
– Exemplos de arredondamentos ao milímetro (a três casas decimais):
•
•
•
•
•
15,6232m → 15,623m
15,6237m → 15,624m
15,6235m → 15,624m
15,6245m → 15,624m
No caso do “5” arredondar
para o par mais próximo!
Medidas angulares com precisão de segundos.
X
– Sem decimas de segundos. CERTO: 124° 23' 34“ ERRADO: 124° 23' 34,23“
– Exemplos de arredondamento ao segundo:
•
•
•
•
•
20⁰30’16,32” → 20⁰30’16”
20⁰30’16,73” → 20⁰30’17”
20⁰30’16,50” → 20⁰30’16”
20⁰30’15,50” → 20⁰30’16”
No caso do “5” arredondar
para o par mais próximo!
Cálculos/valores intermediários
– Usar a precisão total da calculadora e usar a capacidade da calculadora de fazer cálculos complexos de
uma só vez. Porém, nunca use menos de seis casas decimais nos resultados parciais;
• Recomenda-se não copiar resultados intermediários/parciais da calculadora na folha dos cálculos.
• Matematicamente só deve-se indicar o modelo matemático, os valores das variáveis e o resultado final, sem
os resultados parciais (faça os cálculos de uma única vez na calculadora!)
Estas condições de precisões e formalismos serão cobradas nos resultados numéricos das
provas, descontando-se nos cálculos (precisões) e no método (formalismos matemáticos)
Tecla “GRAUS” para trabalhar com graus, minutos e segundos
sexagesimais nos dois formatos usuais (ggg/mm/ss ou g.ddddddd)
Exemplo: calcular o cosseno de 30⁰16’46”:
cos 3
0 ⁰’” 1
6 ⁰’” 4
6
⁰’”
)
=
No ecrã da calculadora resulta:
No mínimo, trabalhar com 6 casas
decimais nas funções trigonométricas, se
necessário valores intermediários. Neste
caso seria: 0,833576
Exemplo: calcular o arco cosseno de 0.923456 (descobrir o ângulo):
SHIFT cos
.
3
6
0
9
2
4
5
)
= ⁰’”
No ecrã da calculadora resulta:
Neste caso, o resultado deve ser
considerado como 22°33’48”
Nunca usar decimas de segundos
Exemplo: calcular a raiz quadrada de 5,32 menos 32 (metros):
5
.
)
3
2
3
=
• (
No ecrã da calculadora resulta:
Observação: os parênteses iniciais nas funções
trigonométricas dependem do modelo de CASIO:
se apertar a função e aparecer a abertura de
parêntese, lembre-se de fechá-lo antes da tecla “=“
Nos resultados finais de comprimento de
segmentos de retas, usar só três casas
decimais: 4,369m neste caso.
Classificações dos ângulos
Com relação às suas medidas
• Giro:
– ângulo que mede 360° (também pode ser chamado de Ângulo de uma volta ou
completo).
– Um ângulo de 360 graus é aquele que completa o círculo.
– A volta completa coincide com o ângulo de 0° mas possui a grandeza de 360°.
– Tal identificação se assemelha à do ângulo negativo com o ângulo positivo que tem como
medida exatamente aquele (negativo) somado com a volta completa.
• Consecutivos:
– dois ângulos são chamados consecutivos se um dos lados de um deles coincide com um
dos lados do outro ângulo;
• Adjacentes:
– Ângulos adjacentes são aqueles que possuem um lado em comum, mas as regiões
determinadas não possuem pontos em comum;
• Opostos:
– Dois ângulos são opostos pelo vértice quando os lados de um deles são semirretas
opostas aos lados do outro.
• Congruentes:
– Dois ângulos são congruente (ou coincidentes) se quando sobrepostos os lados de um
deles são as mesmas semirretas dos lados do outro.
Classificações dos ângulos
Com relação às suas medidas
• Nulo:
– um ângulo nulo mede 0°;
• Agudo:
– ângulo cuja medida é maior do que 0° e menor do que 90°;
• Reto:
– um ângulo reto é um ângulo cuja medida é exatamente 90°; assim os
seus lados estão localizados em retas perpendiculares;
• Obtuso:
– é um ângulo cuja medida está entre 90° e 180°;
• Raso:
– ângulo que mede exatamente 180°, os seus lados são semirretas
opostas;
• Côncavo ou reentrante:
– ângulo que mede mais de 180°e menos de 360°;
Classificações dos ângulos
Quanto a suas complementações
• Complementares:
– dois ângulos são complementares se a soma de suas medidas é
igual a 90°. Neste caso, cada um é o complemento do outro.
• Suplementares:
– dois ângulos são Suplementares quando a soma de suas medidas
é igual a 180°. Neste caso, cada um é o suplemento do outro.
• Explementares:
– Dois ângulos são Explementares quando a diferença de suas
medidas é igual a 180. Neste caso, cada um é o explemento do
outro.
• Replementares:
– dois ângulos são Replementares quando a soma de suas medidas
é igual a 360°. Neste caso, cada um é o replemento do outro.