Coordenadas polares - Páginas Pessoais

Notas de Aulas de Cálculo Diferencial e Integral II– Engenharia de Materiais
Prof.: Adriana Borssoi
1
PR
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Ministério da Educação
Universidade Tecnológica Federal do Paraná
Campus de Londrina
Gerência de Ensino e Pesquisa
Estas Notas de Aulas são organizadas com base
nas referências mencionadas abaixo, de onde
também são extraídos exemplos e exercícios
sugeridos. O material não pretende substituir
um bom livro de Cálculo, mas serve como um
apoio aos alunos no acompanhamento das
aulas.
ENGENHARIA DE MATERIAIS
O livro texto adotado no curso é:
ANTON, H., BIVENS, I. e DAVIS, S.
Cálculo. vol. 2. Tradução: Claus I. Doering. 8
ed. Porto Alegre: Bookman, 2007.
NOTAS DE AULA
CÁLCULO DIFERENCIAL E INTEGRAL II
Como Bibliografia Complementar sugerimos:
LEITHOLD, L. O Cálculo com Geometria
Analítica, vol 1 e 2. Harbra, São Paulo, SP:
1994
FINNEY, R. L; WEIR, M. D; GIORDANO, F.
R. Cálculo de George B. Thomas, vol. 2. 10ª
edição. Trad. Cláudio H. Asano. São Paulo:
Addison Wesley, 2003.
HOFFMANN, Laurence D. Cálculo: um curso
moderno e suas aplicações. Rio de Janeiro:
LTC, 2002.
STEWART, James. Cálculo v. I e II, 5 ed. São
Paulo: Pioneira Thompson Learning, 2006.
LONDRINA
2011
VILCHES, M.A; CORREA, M.L. Cálculo vol.
1 e 2, UFRJ. (Material Eletrônico)
Notas de Aulas de Cálculo Diferencial e Integral II– Engenharia de Materiais
Prof.: Adriana Borssoi
2
1. COORDENADAS POLARES
Exercícios
Recomendados:
ANTON,
H.,
BIVENS, I. e DAVIS, S. Cálculo. vol. 2 Tradução:
Claus I. Doering. 8 ed. Porto Alegre: Bookman,
2007.
Páginas, de 727 à 730
Páginas, de 744 à 746
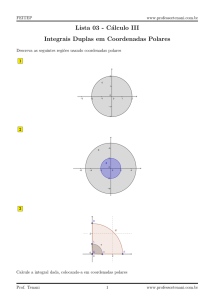
Um método importante de representação de pontos
num plano consiste no uso de coordenadas
polares. Para introduzir um sistema de
coordenadas polares no plano, partimos de um
ponto fixo O, chamado de origem ou pólo, e uma
semirreta orientada, chamada eixo polar, com
extremidade O. Neste sistema a cada ponto P do
plano podemos associar as coordenadas polares
(r ,θ ) onde: r é a distância de O a P; θ é o ângulo
orientado, no sentido anti-horário, desde o eixo até
à semirreta OP.
Sejam ( x, y ) as coordenadas cartesianas e
(r ,θ ) as coordenadas polares de um mesmo
ponto P. Pelas relações descritas acima, temse:
 x = r cos(θ )
 y = rsen(θ )

 x2 + y2 = r 2

 y = tg (θ ), x ≠ 0
 x
Exercícios
E01_Realize as conversões dos pontos:
a) P = (2, π / 3) de c. polares para c.
cartesianas;
b) Q = (1, −1) de c. cartesianas para c. polares.
E02_Encontre a equação cartesiana para a curva
descrita pela equação polar r = 3sen(θ ) .
E03_Encontre a equação polar para x 2 − y 2 = 1 .
Figura 1.1
Se r for negativo, deve-se representar r unidades
na semirreta, com extremidade O e sentido oposto
a OP.
É importante considerar que, quando consideramos
o sistema de coordenadas cartesianas cada ponto
tem representação única. Usando o sistema de
coordenadas polares isto não acontece. Veja:
P = ( r ,θ ) = (− r ,θ + π ) = (r ,θ + 2kπ ) , para k ∈ .
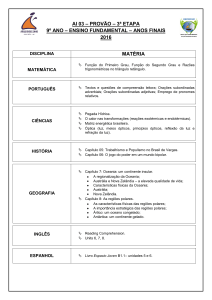
Relação entre Coordenadas Cartesianas e
Coordenadas Polares
A relação entre ambos os sistemas de coordenadas
pode ser obtido por meio da relação de Pitágoras e
trigonometria elementar, considere a Figura 1.2.
Representação Gráfica em Cooedenadas
Polares
Uma mesma curva pode ser representada em
coordenadas cartesianas ou em coordenadas
polares, porém, um sistema de representação
pode ser mais adequado que o outro em
determinadas situações, como será ilustrado em
seguida.
Ao conjunto de pontos (r ,θ ) do plano que
verificam a equação F (r ,θ ) = 0 chama-se
curva em coordenadas polares.
Exemplos: A Figura 1.3 mostra os gráficos
plotado em coordenadas polares. A curva em a)
tem equação polar r1 = 2cos ( 3t ) , sendo que a
correspondente equação cartesiana é dada por
x 4 − 2 x3 + 2 x 2 y 2 + 6 xy 2 + y 4 = 0 (Verifique!).
θ 
A curva em b) tem equação r2 = sen   , com
4
0 ≤ θ ≤ 10π . Como seria sua equação em
coordenadas cartesianas? Seria ela obtida
facilmente?
Figura 1.2
Notas de Aulas de Cálculo Diferencial e Integral II– Engenharia de Materiais
Prof.: Adriana Borssoi
3
a)
ii) r = acos(nθ ) , a > 0
n=2
n=3
b)
y
y
n=4
n=5
x
1
2
x
Figura 1.5
Figura 1.3: Gráficos gerados pelo Winplot 9.0
Vejamos algumas equações polares de retas e
circunferências, escritas de forma geral, com
a∈ :
• Retas verticais: r cos(θ ) = a ou r = a sec(θ )
• Retas horizontais: rsen(θ ) = a ou r = acosec(θ )
• Retas que passam pela origem: θ = θ 0
• Circunferência centrada na origem: r = a
• Circunferência centrada no eixo Ox e tangente ao
eixo Oy: r = 2a cos(θ )
• Circunferência centrada no eixo Oy e tangente ao
eixo Ox: r = 2asen(θ )
Podemos verificar que a expressão em coordenadas
polares fica mais simples, por exemplo, a última
circunferência mencionada acima tem equação
polar r = 2asen(θ ) , enquanto em coordemadas
cartesianas a mesma circunferência teria equação:
x 2 + ( y − a) 2 = a 2 .
Exercício
E04_Esboce o gráfico das equações polares,
plotando pontos:
a) ra = θ
b) rb = sen(θ )
Outras equações serão apresentadas a seguir, a
título de ilustração:
Família de Rosáceas
i) r = asen(nθ ) , a > 0
n=2
n=3
Figura 1.4
n=4
n=5
Exercício
E05_Defina Cardióides e Limaçons, depois use
um recurso computacional, como WinPlot por
exemplo, e ilustre alguns membros de cada
família.
Teste de Simetria para gráficos polares
Teorema
a) uma curva polar é simétrica em relação ao
eixo x se substituindo θ por −θ obtivermos
uma equação equivalente;
b) uma curva polar é simétrica em relação ao
eixo y se substituirmos θ por π − θ
obtivermos uma equação equivalente;
c) uma curva polar é simétrica em relação a
origem se substituirmos θ por π + θ , ou
sbstituírmos r por –r, obtivermos uma equação
equivalente.
Figura 1.6: Ilustração das simetrias indicadas no
teorema.
Exercício
E06_(ANTON, 2007, p.722) Verifique a ocorrêcia
de simetrias no gráfico de r = a − a cos(θ ) ,
depois faça o esboço com a = 1 para confirmar
o resultado.
Retas tangentes a Curvas Polares
A inclinação de uma reta tangente a curvas
polares de equação r = f (θ ) , em que r é uma
função diferenciável de θ é dada por:
dr
dy
r cos(θ ) + sen(θ )
dy
d
θ
d
θ
=
=
dx
dr
dx
dθ −rsen(θ ) + cos(θ )
dθ
A expressão acima decorre do fato que
x = f (θ ) cos(θ ) e y = f (θ )sen(θ ) .
Notas de Aulas de Cálculo Diferencial e Integral II– Engenharia de Materiais
Prof.: Adriana Borssoi
4
y
Exercício
E07_(ANTON, 2007, p.734): Encontre a inclinação da
reta tangente ao círculo r = 4cos(θ ) no ponto em
que θ =
π
4
x
.
1
Área em Coordenadas Polares
Definição: Se α e β forem ângulos que
satisfaçam a condição α < β ≤ α + 2π e se f (θ )
for contínua e não-negativa para α ≤ θ ≤ β , então
a área A da região R envolvida pela curva polar
r = f (θ ) ( α ≤ θ ≤ β ) e os raios θ = α e θ = β é
β
β
1
1 2
A=
r dθ .
[ f (θ )]2 dθ =
2
2α
α
∫
(Veja interpretação
fórmula).
∫
geométrica e
deduza
a
Os extremos de integração podem ser
determinados seguindo os procedimentos:
i) Esboçar a região R do plano, cuja área se deseja
determinar;
ii) Desenhar uma linha radial arbitrária do pólo até
a curva r = f (θ ) da franteira;
iii) Avaliar sobre qual intervalo θ deve variar para
que a reta radial varra a região R;
iv) Os extremos do intervalo fechado obtido no
item iii) são os extremos de integração.
Exercícios
E08_(ANTON, 2007, p.742): Determine a área da
região do primeiro quadrante dentro da cardióide
3
r = 1 − cos(θ ) . (Resp. π − 1 )
8
E09_(ANTON, 2007, p.742): Determine a área interna
3
à cardióide do exercício anterior. (Resp. π )
2
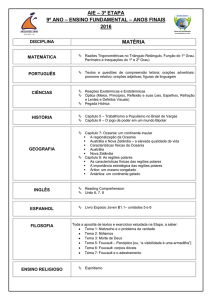
E10_(ANTON, 2007, p.743): Determine a área da
região que está dentro da cardióide r = 4 + 4cos(θ )
e fora do círculo r = 6 . (Resp. 18 3 − 4π )
2
3
4
5
6
7
8
9
Figura 1.7: Representação gráfica das curvas
polares do exercício E10.