Lista 03 - Cálculo III Integrais Duplas em

Propaganda

FEITEP
www.professortenani.com.br
Lista 03 - Cálculo III
Integrais Duplas em Coordenadas Polares
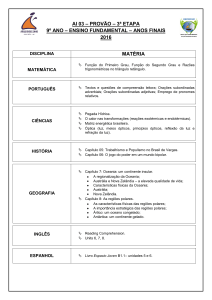
Descreva as seguintes regiões usando coordenadas polares
1
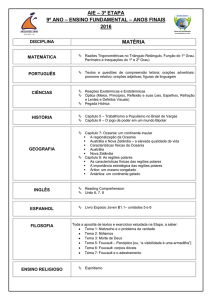
2
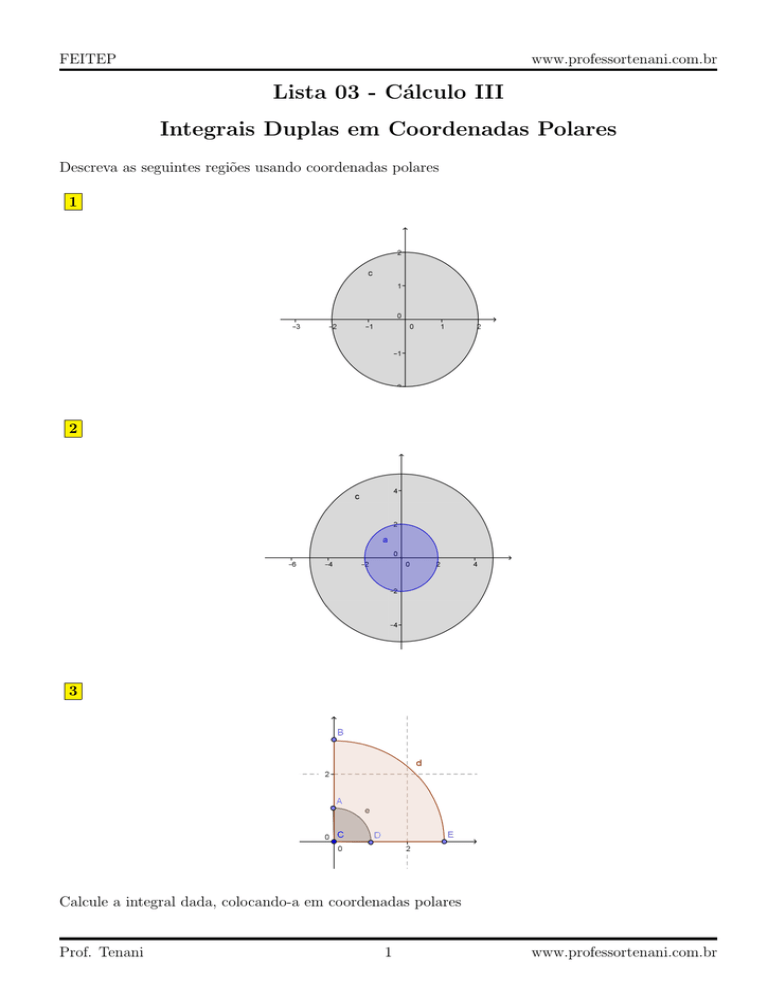
3
Calcule a integral dada, colocando-a em coordenadas polares
Prof. Tenani
1
www.professortenani.com.br
FEITEP
www.professortenani.com.br
ZZ
4
∗
xy dA onde R é o disco com centro na origem e raio 3.
R
ZZ
5
(x + y) dA onde R é a região que está a esquerda do eixo y e entre as circunferências
R
x2 + y 2 = 1 e x2 + y 2 = 4.
ZZ
6
cos(x2 + y 2 ) dA onde R é a região que está acima do eixo x e dentro da circunferência
R
x2 + y 2 = 9.
ZZ
2
2
e−x −y dA onde R é a região que está a direita do eixo y e dentro da circunferência
7
R
x2 + y 2 = 4.
Utilize coordendas polares para determinar o volume do sólido dado.
8 ∗ Abaixo do parabolóide z = x2 + y 2 e acima do disco x2 + y 2 ≤ 9.
GABARITO
1)
R = {(r, θ) 0 ≤ r ≤ 2, 0 ≤ θ ≤ 2π}
2)
R = {(r, θ) 2 ≤ r ≤ 5, 0 ≤ θ ≤ 2π}
3)
4)
R = {(r, θ) 1 ≤ r ≤ 3, 0 ≤ θ ≤
π
}
2
14
3
5)
−
6)
π
sen9
2
7)
π
(1 − e−4 )
2
8)
81π
2
0
OBS: Os exercı́cios marcados com * devem ser entregues na forma de trabalho
Prof. Tenani
2
www.professortenani.com.br