Clique aqui para abrir

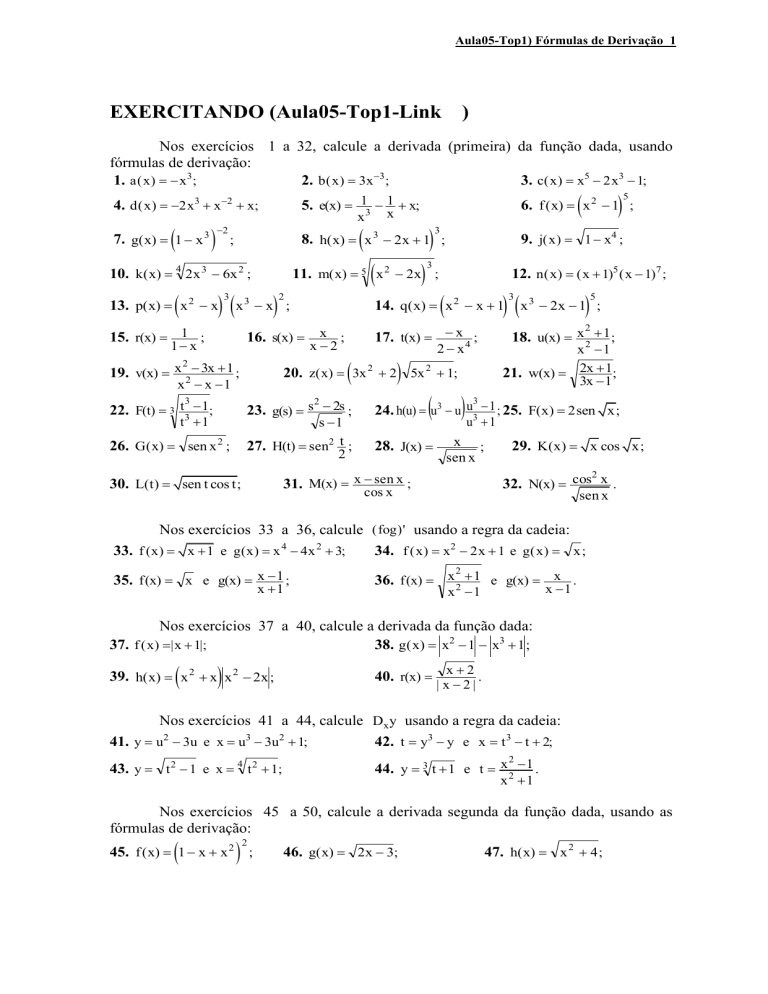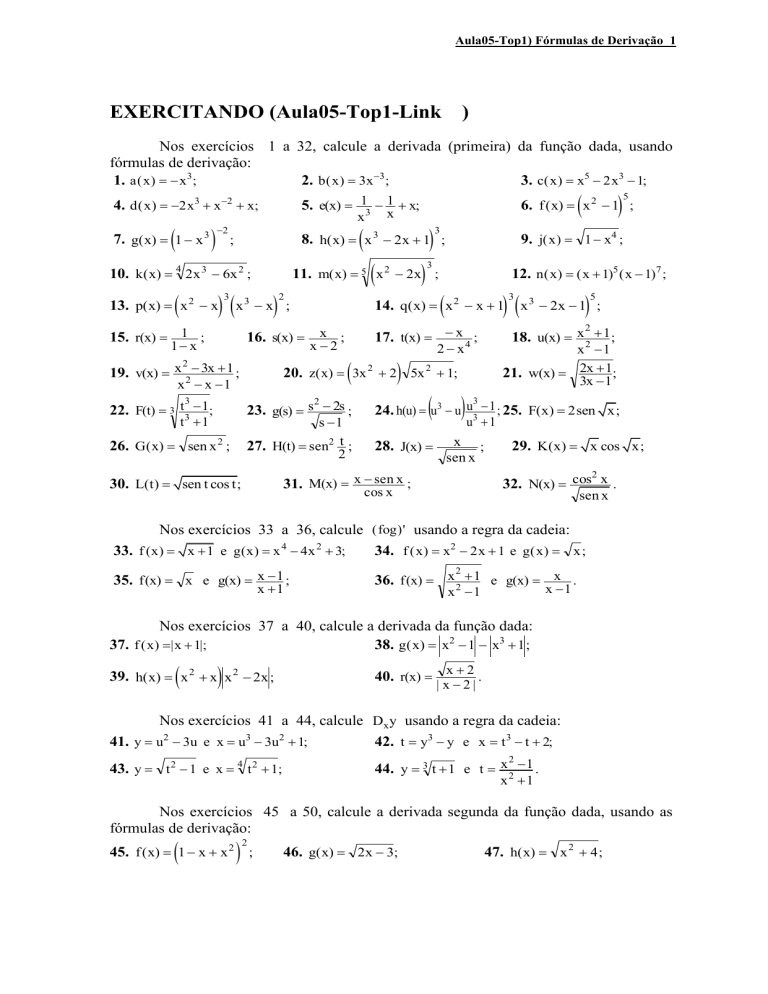
Aula05-Top1) Fórmulas de Derivação 1
EXERCITANDO (Aula05-Top1-Link
)
Nos exercícios 1 a 32, calcule a derivada (primeira) da função dada, usando
fórmulas de derivação:
1. a ( x )   x3 ;
2. b ( x )  3x 3 ;
3. c( x )  x5  2 x3  1;
4. d ( x )  2 x3  x2  x;

7. g( x)  1  x

3 2



3

 x
3
15. r(x)  1 ;
3

2x

2
23. g(s)  s  2s ;
s 1
27. H(t)  sen2 t ;
2
3

5
 2x  1 ;
 u  1
x 1
21. w(x)  2x  1;
3x  1
3
24. h(u)  u3  u u3  1 ; 25. F(x)  2sen x;
28. J(x) 
x ;
sen x
31. M(x)  x  sen x ;
30. L(t)  sen t cos t;
3
2
18. u(x)  x 2  1 ;
20. z( x)  3x 2  2 5x 2  1;
x  x 1
26. G( x)  sen x 2 ;
 x
17. t(x)   x 4 ;

19. v(x)  x 2  3x  1 ;
t 1
12. n ( x)  ( x  1)5 ( x  1)7 ;
14. q( x)  x 2  x  1
x2
2
3
22. F(t)  3 t3  1;
3

2
16. s(x)  x ;
1 x

11. m( x)  5 x 2  2 x ;
x ;
5
9. j( x )  1  x4 ;
8. h( x)  x 3  2x  1 ;
;

6. f ( x)  x 2  1 ;
x
x
10. k ( x)  4 2 x 3  6x 2 ;
13. p( x)  x 2  x

5. e(x)  13  1  x;
29. K(x)  x cos x;
2
32. N(x)  cos x .
cos x
sen x
Nos exercícios 33 a 36, calcule ( fog )' usando a regra da cadeia:
33. f (x)  x  1 e g(x)  x 4  4x 2  3;
34. f ( x )  x2  2 x  1 e g ( x )  x ;
35. f (x)  x e g(x)  x  1 ;
x 1
2
36. f (x)  x 2  1 e g(x)  x .
x 1
x 1
Nos exercícios 37 a 40, calcule a derivada da função dada:
37. f ( x) | x  1|;
38. g( x)  x2  1  x3  1 ;


39. h( x)  x 2  x x 2  2x ;
x2
.
40. r(x) 
|x2|
Nos exercícios 41 a 44, calcule Dx y usando a regra da cadeia:
41. y  u2  3u e x  u3  3u2  1;
42. t  y3  y e x  t 3  t  2;
43. y  t 2  1 e x  4 t 2  1;
2
44. y  3 t  1 e t  x 2  1 .
x 1
Nos exercícios 45 a 50, calcule a derivada segunda da função dada, usando as
fórmulas de derivação:


2
45. f ( x)  1  x  x 2 ;
46. g( x)  2x  3;
47. h( x)  x 2  4 ;
Aula05-Top1) Fórmulas de Derivação 2
48. p(u )  (u  1) 3 (u 3  1);
t ;
2t  1
49. q(t) 
50. J(t) 
sen t .
(1  cos t)2
51. Se f ( x)  3 x 3  3x , calcule f (3) (x).
Nos exercícios 52 e 53, encontre as equações das retas (i) tangente e (ii)
normal ao gráfico da equação dada no ponto indicado:
52. y  x2 1 , (0,1);
53. y  x 2 sen x  x cos 2 x, (0,0);
x 1
Nos exercícios 54 e 55, determine os pontos dos gráficos das equações dadas,
onde a reta tangente é horizontal:
54. y  2 x 3  1 x 2;
55. y  4 x3  3x2  6 x  2;
3
2
Nos exercícios 56 a 59, a equação dada é de uma partícula que se desloca s
quilômetros em t horas, ao longo de uma reta horizontal. Determine: (a) Os instantes em
que a partícula está em repouso; (b) Os intervalos de tempo em que a partícula se move
para direita ou para esquerda:
2
57. s  t ;
56. s  4t3  15t 2  12t  10
t 1
59. s  (1  sen t ) cos t, t  2.
58. s  t  sen t, t  2;
60. Uma partícula se desloca em movimento retilíneo e tem equação de movimento
s  sen t  sen42t para t  2, calcular os intervalos de tempo em que sua velocidade
está diminuindo ou aumentando.


61. Se f ( x)  x2  1 e g( x)  f x 2  1 , calcule g' ( x ).
62. Se ( fog )( x )  x2  x  1 e g ( x )  x , mostre que f ' ( x )  4 x 3  2x.
63. Se g é uma função derivável, g'( 2 )  4 e f (x)  g  x  , calcule f ' (4).
64. Se f é uma função derivável, f ' (1)  f " (1)  1 e g(x)  f  x 3  , calcule g"(1).
65. Sejam f e g funções deriváveis, tais que ( fog )( x )  x e f ( x)  f ' ( x) para todo x,
mostre que g' (x)  1x para todo x  0.
66. Sendio f uma função derivável, mostre que:
(a) Se f é par, então f ' é ímpar e f ' (0)  0;
(b) Se f é ímpar, então f ' é par.
67. Sejam f e g funções deriváveis. Se g é par e h  fog , mostre que h' é ímpar e
h'( 0)  0.
Aula05-Top1) Fórmulas de Derivação 3
68. Se f é uma função derivável tal que f ( u )  f ( v)  f ( uv ) para todo u e v, mostre que
 
f ' ( x)  xf ' x 2  0.
69. Se f é uma função derivável tal que f ( u  v )  f ( u ) f ( v ) para todo u e v, mostre que
f ( x) f '( x)  f ' (2x)  0.
 f '
1
70. Seja f uma função tal que f ' é derivável e f ' ( x)  0. Se
(
- f " f - 1 (x)
que (f - 1 )"(x) =
)
3
éf ' f - 1 (x) ù
êë
ú
û
(
)
é derivável, mostre
.
RESPOSTAS (Exercícios ímpares)
1. a´(x)  3x 2 ; 3. c´(x)  5x 4  6x 2 ; 5. e '(x)   34  12  1; 7. g '(x) 
x
6(x  1)
3
9. j'(x)  2x ; 11. m '(x) 
1 x
4
5
5

13. p' ( x)  x 2  x
 x
2
15. r '(x)  1 2 ;
(1  x)
21. w' (x) 
3
 
x
2
 2x

2

x
 

 3x 4  2
2

2x x  2
x
39. h '(x) 
43. D x y 
49. q" ( t ) 
x 2
2
2

2  x 
4 2
19. v '(x) 
;



2 x
;
35. (fog)' (x) 

t 1
2t
(2t  1)
5
;
;




59. (a)

2

2
51. f (3) (x) 
3
31. M(x)  cos x  x 2sen x  1 ;
cos x
h, (b) Somente para direita;
37. f ' (x)  x  1 ;
| x 1 |
41. Dx y  2u  3 ;
3u(u  2)
47. h "(x) 

 12 , 154  ;
4
x
2
4

3
;
  6x  x 2  1  1 ;
2
3
 x  3x 
 5 x2 1

 3
 x  3x
2
 x3  3x  
55. (1,3) e

;
2
 x 2  x  1
x
1
;
(x  1)(x  1)3
45. f "( x)  6 1  2x  2x 2 ;
53. (i) x  y  0, (ii) x  y  0;
direita;

3
2

25. F(x)  cos x ;
 2x 2x x 2  1  (2x  1) x 2  2x 

;
2
x  2x
24 t 2  1
;
2 x 2  2x  2
27. H(t)  sen t ; 29. K(x)  1 cos x  x sen x ;
33. (fog) '(x) 
3
;
3x  1 ; 23. g' (s)  3s2  6s  4 ;
2x  1
2 (s  1)3
2
1  x3 
 x 2 x 2  x 3x 2  1  3 x 3  x 2 x  1 ;
17. t' ( x ) 
5
2(3x  1)2
6x 2
3
57. (a) 0 h , (b) Somente para
61. g' ( x )  4x 3  2x;
63. f ' (4)  1.