Função Quadrática Facer (140288)

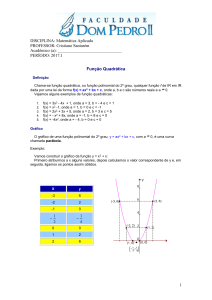
Funções
FUNÇÃO DO 2º GRAU OU QUADRÁTICA
Dados os números reais a e b, com a  0, chama-se função do 2º grau ou
f :    , definida por y = ax2 + bx + c
função quadrática a função
ou
f(x) = ax2 + bx + c.
Exemplos
a) f(x) = x2 – 4x – 3
a = ____ b =____ c =____
b) y = x2 – 9
a = ____ b =____ c =____
c) g(x) = – 4x2 + 2x – 3
a = ____ b =____ c =____
d) h(x) = x2 + 7x
a = ____ b =____ c =____
Exercício: Sendo f(x) = (m + 5)x2 + 2x – 4, determina m de modo que:
a) f(x) seja do 2º grau
b) f(x) seja do 1º grau
Gráfico da função quadrática
O gráfico de uma função do 2º grau é uma curva denominada parábola. Seu
domínio é o conjunto dos números reais e sua imagem é um subconjunto dos números
reais. Ou seja, Dom f=  e Im f   .
Exemplos
Constrói o gráfico das seguintes funções:
a) f(x) = x2
b) g(x) = – x2
Concavidade
O sinal de a (coeficiente de x2) determina a concavidade da parábola. Assim:
 Se a > 0 (a positivo), a concavidade é voltada para cima: 
 Se a < 0 (a negativo), a concavidade é voltada para baixo: 
Podemos verificar isto nos exemplos anteriores, onde f(x) tem concavidade
voltada para cima, pois a = 1 e g(x) tem concavidade voltada para baixo, pois a = – 1.
Zeros (ou raízes) de uma função do 2º grau
Denominam-se zeros ou raízes de uma função quadrática os valores de x que
anulam a função, ou seja, que tornam f(x) = 0. Em termos de representação gráfica,
são as abscissas dos pontos onde a parábola corta o eixo x.
Denomina-se equação do 2º grau com uma variável toda equação da forma
ax2 + bx + c = 0 , onde x é a variável e a, b, c   com a  0.
Oservação: c é a ordenada do ponto (0, c), onde a parábola corta o eixo y.
Exemplos
a) 2x2 – 3x + 1 = 0
a = 2;
b) x2 – 4 = 0
b = -3;
a = 1;
c=1
b = 0;
c) y2 + 3y = 0
a = 1;
b = 3;
c=0
d) 5x2 = 0
a = 5;
b = 0;
c=0
c = -4
Resolução de Equações do 2º Grau
Resolver uma equação significa determinar o conjunto solução (ou conjunto
verdade) dessa equação. Para a resolução das equações do 2º grau, utilizamos a
Fórmula Resolutiva ou Fórmula de Báskara dada abaixo:
Se ax2 + bx + c = 0 e a  0, então
x 
b  
2a
, onde
  b2  4ac
  0
  0
 Se   0 a equação tem raízes reais 
 Se   0 a equação não tem raízes reais.
Exemplos: Dada a função f, calcular os zeros desta função.
a) f(x) = 2x2 – 3x + 1
b) h(x) = x2 – 4
d) y = 5x2
e) g(x) = x2 – 5x + 7
c) g(x) = x2 + 3x
f) y = x2 – 6x + 9
Vértice da Parábola
Toda parábola tem um ponto de ordenada máxima ou um ponto de ordenada
mínima. A esse ponto chamaremos vértice da parábola e o representaremos por
V(xv,yv) onde
xv  
b
2a
e
yv  

4a
 
 b
V 
,

 2a 4a 
Assim:
ordenada do vértice
abscissa do vértice
Exemplo
Determinar as coordenadas do vértice V da parábola que representa a função
f ( x )  x 2  3x  2
Exercícios
1)
Dada a função f, calcular os zeros desta função e representar graficamente:
a) f ( x )  x 2  7 x  6
b) f ( x )  x 2  2x  6
c) f ( x )   x 2  2x  1
d) f ( x )  x 2  3
e) f ( x )   x 2  36
f)
f ( x )  ( x  4) 2
g) f ( x )  ( x  9) 2
2)
Sendo f ( x ) 
a) f(3)
3 x 2  3 x  3 calcular:
b)
f (3 )  f ( 3 )
3 3
3)
Dadas as funções reais f(x) = x2 – 1 e g(x) = –x2, calcular o valor de f(–1).g(–2).
4)
Sendo f(x) = x2 + 2x – 1 e g(x) = x2 , determinar os valores de x para os quais
f(x) = g(x).
Valor máximo e valor mínimo da função do 2º grau
Examinando os gráficos abaixo, observa-se que:
y
y
yv
V
0
xv
xv
x
0
yv
x
V

é o valor
4a
mínimo da função.
Se a > 0, yv  
Se a < 0, yv  

é o valor
4a
máximo da função.
Exemplos
1)
A função f(x) = x2 – x – 6 admite valor máximo ou valor mínimo? Qual é esse
valor?
2)
Os lados de um terreno retangular medem x e y (em metros). Sabendo que o
perímetro desse retângulo é de 20m:
a) determinar sua área em função de um dos lados;
b) construa o gráfico dessa função;
c) verifique as dimensões para que o terreno tenha área máxima.
LISTA COMPLEMENTAR DE EXERCÍCIOS
1) Sendo f :    uma função definida por f(x) = x2 – 1, calcular:
1
2
a) f  

b) f 1  2

2) Dada a função f(x) = x2 + 4x + 4, calcular k para que f(k – 1) = 0.
3) Determinar os valores de p para os quais a função f(x) = (4 – 8p)x2 + x – 7 é
quadrática.
4) Determinar os zeros das funções abaixo:
a) f(x) = 6x2 + 5x – 4
b) f(x) = – x2 – 2x – 1
c) f(x) = x2 – 3
d) y = x(2x – 1) + 3(x – 3) – x2
5) Determine os valores de m para os quais a equação a seguir admita duas raízes
iguais: x2 + (m + 2).x + (2m + 1) = 0
6) Determine o valor máximo ou mínimo de cada uma das funções em .
a) f(x) = – 3x2 + x + 2
b) f(x) = x2 – 2x + 4
c) f(x) = x2 + 5x
d) f(x) = 4 – x2
7) O vértice da parábola y = x2 – 4x + 1 está no ponto (2, b). Calcular b.
8) Fazer o gráfico cartesiano e dar o domínio, a imagem, as raízes, o valor de
máximo ou de mínimo das funções abaixo:
a) y = x2 – 6x + 5
b) f(x) = – 2x2 + 6x
y
c) g(x) = 3x2
d) h(x) = 2x2 – 8
4
3
9) Dado o gráfico ao lado, determinar:
a) as raízes da f;
b) f (1);
c) os valores de “x” tais que f(x) = 4;
-2
0
1
2
10) Um terreno de forma retangular tem perímetro igual a 40 m.
a) Expressar a área desse terreno em função do comprimento de um dos lados.
b) Construir o gráfico dessa função.
c) Calcular as dimensões desse terreno para que a área seja máxima.
11) Dada à função representada pelo gráfico
y abaixo determinar zeros da função as
coordenadas do vértice.
-4
-3
-1
1
x
-2
12) Seja f(x) = mx2 + nx +3. Determinar m e n, sabendo que f(1) = f(3) = 0.
x