Função afim: a função geral de 1º grau

Função quadrática:
a função geral de 2º grau
Função quadrática ou função de 2º grau é toda
função do tipo
y = f(x) = ax2 + bx + c
Sendo a, b e c são constantes reais, com a ≠ 0.
O Domínio de toda função quadrática é IR.
Exemplos

y = f(x) = x2 + 3x – 1
é uma função quadrática com a = 1 e b = 3 e c = –1.

y = f(x) = –x2 + 5
é uma função quadrática com a = –1 e b = 0 e c = 5.

y = f(x) = –2x2 + 4x
é uma função quadrática com a = –2 e b = 4 e c = 0.

y = f(x) = x2
é uma função quadrática com a = 1 e b = 0 e c = 0.
Uma quadra esportiva tem a forma retangular,
com 40 m de comprimento e 20 m de largura.
O clube pretende ampliá-la. Para isso, vai
construir em volta dela uma faixa de largura
constante.
Obter a expressão que permite calcular a Área da
quadra esportiva?
x
40 m
20 m
x
x
A = (40 + 2x).(20+2x)
x
⇒ A = 800 + 80x + 40x + 4x2
⇒ A = f(x) = 4x2 + 120x + 800
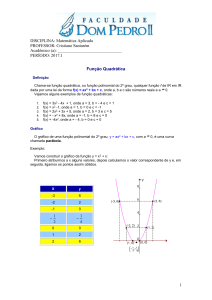
Veja seus gráficos

y
y = x2.
5
x
y = x2
4
–2
4
3
–1
1
2
0
0
1
1
2
4
y = x2
1
x
–5 –4
–3
–2
–1
0
1
2
3
4
5
–1
–2
Im = [0, +∞[
Mínimo = 0
Veja seus gráficos

y
y = – x2.
x
y = – x2
–2
–4
–1
–1
0
0
1
–1
2
–4
x
0
–5 –4
–3
–2
–1
1
2
3
4
5
–1
–2
–3
–4
Im = ]– ∞, 0]
y = – x2
Máximo = 0
A análise das duas últimas figuras nos sugere um caso
geral em relação a todas as funções quadráticas do tipo
y = f(x) = ax2 + bx + c.





Os gráficos de funções quadráticas são curvas
chamadas parábolas.
O ponto mais alto ou mais baixo da parábola é
chamado de vértice.
A reta vertical que passa pelo vértice é chamada de eixo
da parábola.
Se a > 0 a concavidade da parábola é voltada para cima.
Se a < 0 a concavidade da parábola é voltada para
baixo.
Eixo de simetria.
eixo de simetria
da parábola
V
A
B
C
D
A1
r1
B1
C1
D1
r2
r3
r4
Raízes da função
quadrática
Já sabemos que as raízes de uma função real y = f(x)
são os valores de x tais que y = 0. São as abscissas dos
pontos em que o gráfico de f corta o eixo das abscissas.
Na função quadrática y = ax2 + bx + c (a ≠ 0), achar as
raízes significa resolver a equação de 2º grau f(x) = 0.
Número de raízes da equação de 2º grau

Para resolver uma equação de 2º grau usamos a fórmula de
Bhaskara
x
b 
2a
sendo  = b2 – 4ac
O número real  é o discriminante da equação. O valor dele
indica se a função tem ou não raízes reais.
  > 0 ⇔ tem duas raízes reais distintas.
  = 0 ⇔ tem duas raízes reais iguais
(ou 1 raiz real dupla).
  < 0 ⇔ não tem raízes reais.
Exemplo

Um objeto é atirado para cima, da janela situada no alto de um prédio
de 80 m de altura. Sua velocidade inicial é de 30 m/s. A altura h do
objeto em relação ao solo, em metros, t segundos após o lançamento, é
h(t) = 80 + 30t – 5t2. Obter:
A) o instante em que o objeto atinge a altura máxima;
B) a altura máxima que ele atinge;
C) o instante em que ele atinge o solo.
Veja o gráfico da função
h(t) = –5t2 – 30t + 80
h (m)
125
80
0
3
8
t (s)