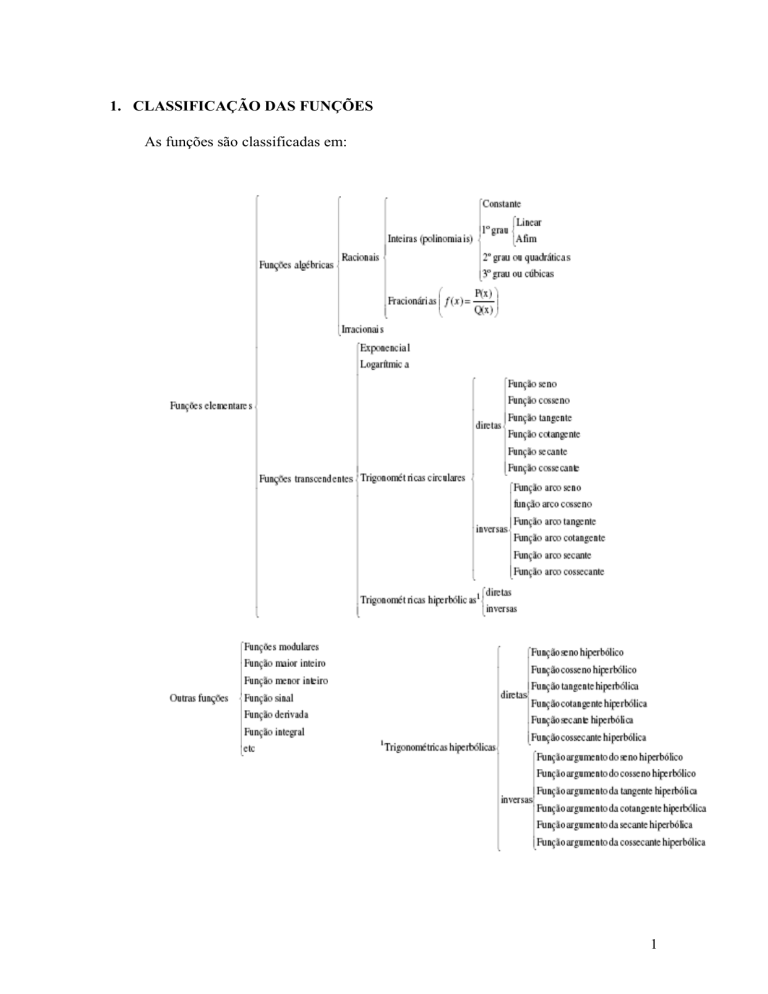
1. CLASSIFICAÇÃO DAS FUNÇÕES
As funções são classificadas em:
1
I) FUNÇÃO DO 1º GRAU
Função do 1º grau é toda função que associa a cada número real x, o número ax + b,
com a ≠ 0. Os números reais a e b são chamados coeficientes angular e linear,
respectivamente.
a > 0 f(x) = ax + b é crescente [f(x) cresce com x]
a < 0 f(x) = ax + b é decrescente [f(x) decresce com x]
O gráfico da função f(x) = ax + b é uma reta não paralela aos eixos coordenados.
D( f ) e Im( f )
a
y 2 y1
(coeficiente angular da reta)
x 2 x1
Exemplos:
a) f(x) = 2x + 3
b) f(x) = -3x + 1
II) FUNÇÃO QUADRÁTICA
Função definida por f(x) = ax2 + bx + c, com a ≠ 0. O gráfico de uma função quadrática
é uma parábola com o eixo de simetria paralelo ao eixo y.
Se a > 0, a concavidade da parábola está voltada para cima. Se a < 0, a concavidade está
voltada para baixo.
Exemplos:
2
a) f(x) = - x2 + 2x – 1
x1 = x2 = 1
b) f(x) = x2 – 2x + 4
= -12
c) f(x) = x2 -2x – 3
x1 = 3 e x2 = -1
Zeros ou raízes da função:
a) < 0 f(x) não tem zero real
b) = 0 f(x) tem zero real duplo
c) > 0 f(x) tem dois zeros reais desiguais
Gráfico da função:
a) < 0 gráfico não toca o eixo dos x
b) = 0 gráfico tangencia o eixo dos x
c) > 0 gráfico corta o eixo dos x
xv
Coordenadas do vértice da parábola:
Soma das raízes: S
b
a
b
2a
Produto das raízes: P
e
yv
4a
c
a
O domínio é igual a , ou seja, D( f )
A Im( f ) depende do vértice em y e do sinal de a:
a) a > 0 Im( f ) y / y
4a
fx x 2 2 x 3 , então Im fx 4,
b) a < 0 Im( f ) y / y
4a
fx x 2 2 x 1 , então Im fx , 0
Exemplo
y = x2 + 2x – 3
a>0
y = -x² – 2x + 3
a<0
3
III) FUNÇÃO POLINOMIAL
Função definida por uma equação da forma f ( x) a0 a1 x a2 x 2 an1 x n1 an x n ,
onde n é um inteiro não negativo e os coeficientes a0 , a1 , a2 an são números reais
constantes. Se an ≠ 0 diz-se que esta função polinomial é de grau n.
Exemplos de gráficos da função polinomial:
y = x3 – x
:
y = x4 – 5x² + 4
Exemplo:
a) f(x) = 7 + 5x - 3x2 – 8x3
(grau 3)
b) f(x) = a0
(função constante) Exemplo função constante: f(x) = 7
c) f(x) = x
(função identidade)
d) f(x) = 5x5 – 6x +7
(grau 5)
IV) FUNÇÕES RACIONAIS
A soma, diferença ou produto de duas funções polinomiais é ainda uma função
polinomial, mas o quociente de duas polinomiais não é, geralmente, uma função
polinomial.
Função racional é definida como o quociente de duas funções polinomiais, ou seja,
f ( x)
p ( x)
onde q(x) não é uma função constante nula.
q( x)
O domínio consiste em todos os valores de x para os quais q(x) ≠ 0.
Exemplos:
a) f(x) = 1/x
Dx 0
4
b)
Dx 1
c)
x 3x 4x 9
Dx 4, -3, 3
x x 12 x 3
x 3x 4 x 9 (x 1 ) (x 4 ) (x-3 ) (x 3 ) x 1
f(x)
(x 4 ) (x-3 )(x 3 )
x x 12 x 3
2
f ( x)
2
2
2
2
2
V) FUNÇÃO IRRACIONAL
Uma função f, real de variável real, chama-se função irracional se a variável
independente figura no radicando. No cálculo do domínio de uma função irracional do
tipo f (x ) n a (x ) , onde n R é necessário ter em atenção que:
Se n é par,
D f x / a (x) 0
Se n é ímpar, não existe qualquer restrição, é .
5
Exemplo Analise o domínio, a imagem e esboce o gráfico da função y 2 x 4 .
Solução:
Neste caso, temos uma função irracional, isto é, a variável está no
radicando. A restrição é que:
2x – 4 0
x2
=>
D = { x R / x 2} ou
D = [2 , )
Im = {y R / y 0} ou
Im = [0 , )
EXERCÍCIOS PROPOSTOS
1) Analise o gráfico das seguintes funções determinando o domínio.
a) y = 5x – 2
b) f(x) = 3
c) f(x) = x
d) y = -x + 6
e) f ( x)
1 2
x 8
2
f) f (x) = 6 – 5x + x²
g) f ( x)
2
x 3
h) y= 8x 5
g) f ( x)
2
x 3
g) f ( x)
x2 9
x3
g) f ( x)
4x
x3
g) f ( x)
x 2 5x 6
x3
g) f ( x)
12
( x 3)( x 1)
g) f ( x)
22
x3
g) f ( x)
2x 2
x3
g) f ( x)
x 2 2 x 15
x3
i) y =
x 2 16
j) y =
x 2 5x 4
6
2) Determine o domínio das seguintes funções:
a) f ( x) 4 x 5
3
b) f ( x) 2
x 1
c) y 1 2 x
x 1
1
7x
x3
4 x x2
d) f ( x)
x 2 5x 4
e) f(x) =
f) f(x) =
4 x2
1
2x 3
5x 3
5x
x7
g) f(x) =
3
2x 8
2x 4
1 x
3
D=R
D = R – {-1, 1}
1
D x R | x
2
D x R | 3 x 4, e, x 2
D(f) = {x IR/-2 <x 1 ou 2 < x 4}
D(f) = {x IR/x -3/2 }
D(f) = {x IR/ x < 1 e x - 4}
7