Aula 1(slides) - UFRJ-HidrodinÂmica Meteorologia

Hidrodinâmica
Aula 01
(10 Sem./2017)
1
Parte I – Movimento Relativo: referenciais
acelerados
Motivação: o estudo da circulação global das grandes massas de ar atmosférico e das
correntes oceânicas se faz a partir de sistemas de observação (referenciais) fixos na Terra.
Esses sistemas de referência são acelerados (não - inerciais). As equações de movimento
(segunda lei de Newton) precisam ser adaptadas à estes referenciais.
2
Movimento Relativo: sistemas de referência
(aproximação não-relativística)
Velocidade:

*

r (t )  r (t )  h (t )

*

dr
dr dh


dt
dt dt
*  
u  u  uh
3
Aceleração:


*

2 *
2
2
du
du duh
d r
d r d h


 2  2  2
dt
dt
dt
dt
dt
dt
 * 
a  a  ah
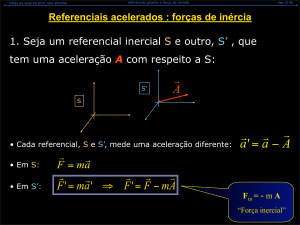
Se O é um referencial inercial
2ª Lei de Newton no referencial
acelerado O*

*

m.a  m.a  mah
 
m.a  F

F , resultante de forças
* 

m.a  F  m.ah
4
Na aproximação não-relativística assumimos que:
- as velocidades envolvidas são muito menores que a
velocidade da luz (c = 3x108 m/s);
- o tempo é uma grandeza absoluta, não dependendo do
referencial considerado;
- a massa é uma grandeza absoluta, independente do
estado de movimento do corpo em observação
5
* 

m.a  F  m.ah
Força fictícia ou
Força inercial.
* 

m.a  F  m.ah  0  0  0
* 


m.a  F  m.ah  m.ah
*

a   ah
6
Sistema de Coordenadas Girantes;
Referenciais Girantes.
sistema - O
iˆ, ˆj , kˆ  (eˆ1 , eˆ2 , eˆ3 )


B  B1.eˆ1  B2 .eˆ2  B3 .eˆ3
sistema - O *
iˆ* , ˆj * , kˆ*  (eˆ1* , eˆ2* , eˆ3* )

B  B1* .eˆ1*  B2* .eˆ2*  B3* .eˆ3*


7

iˆ.B  B1  B1* .(iˆ.iˆ* ) B2* .(iˆ. ˆj * )  B3* .(iˆ.kˆ* );

ˆj.B  B2  B1* .( ˆj.iˆ* )  B2* .( ˆj. ˆj * )  B3* .( ˆj.kˆ* );

ˆ
k .B  B3  B1* .(kˆ.iˆ* )  B2* .(kˆ. ˆj * )  B3* .(kˆ.kˆ* ).


iˆ.iˆ*  iˆ . iˆ* .cos x1 , x1*  1.1.cos11   a11
B1  B1* .cos(11 )  B2* .cos(12 )  B3* .cos(13 )
...
B1  B1* .a11  B2* .a12  B3* .a13
8
aij  cos ij 
3
Bi   B *j .aij , i  1,2,3
j 1
Notação do somatório:
Bi  aij .B*j
j é o índice mudo: subentende uma soma de 1 a 3.
9
Derivada temporal:



dB
B(t  t )  B(t ) 
 lim
B

t

0
dt
t

B  B1.eˆ1  B2 .eˆ2  B3 .eˆ3  Bi .eˆi
ou
B  Bi* .eˆi*

dB 
 B i .eˆi  eˆi são constantes em O.
dt

*
d B  *
 B i .eˆi*  derivada temporal em O*,
dt
eˆi* são constantes em O * .
10
No sistema O, podemos escrever:

*
ˆ
d
(
e
dB d ( Bi* .eˆi* ) d ( Bi* ) *
*
i )
ˆ


.ei  Bi .
dt
dt
dt
dt
(soma em i de 1 à 3)
Considere que o sistema O* gira
em torno do sistema O com velocidade
angular  como indicado na figura
ao lado:
11
Se o vetor B está fixo em
O* podemos concluir que:

d *B
0
dt

dB  
B
dt
(1.1)
12

d (eˆi* )
dB d ( Bi* .eˆi* ) d ( Bi* )


.eˆi*  Bi* .
dt
dt
dt
dt


dB d ( Bi* )

.eˆi*  Bi* .(  eˆi* )
dt
dt


dB d * B  

   B (2.1)
dt
dt
Relação fundamental, válida mesmo na situação
em que  não seja constante no tempo. Se B é
constante no sistema O* a relação 2.1 se reduz
a relação 1.1.
13
A derivada segunda:


*
d  dB  d  d B   
  
   B 



dt  dt  dt  dt



2
*
d B d d B d  
  (  B) (3.1)
 
2
dt
dt  dt  dt



*
*2
*
d d B d B  d B



(4.1)
2


dt  dt  dt
dt


*
d   d (  B)   
(  B) 
   (  B)
dt
dt


*

 d B d *    
d 
(  B)   

 B    (  B) (5.1)
dt
dt
dt
14
Substituindo 5.1 e 4.1 em 3.1 obtemos o seguinte resultado:



*2
*
*
 d B d    
d B d B

 2. 

 B    (  B )
2
2
dt
dt
dt
dt
Por sua vez, temos que,

*
*
d d    d 

   
dt
dt
dt


Se assumimos que B é o vetor posição (r ) de uma particula,
2


*2 
*
 d r d    
d r d r


2
.



 r    (  r )
2
2
dt
dt
dt
dt
2
Teorema de Coriolis
15
Teorema de Coriolis




 d * r d    
d 2 r d *2 r
 2  2. 

 r    (  r )
2
dt
dt
dt
dt

 d *r
2. 
 aceleração de Coriolis
dt

 
  (  r )  aceleração centripeta
16
Se o sistema O é um referencial inercial,
 
d r
m. 2  F , resultante de forças sobre a particula de massa m.
dt
2
Podemos escrever para o referencial girante o seguinte
resultado final:



  
 d *r
d *2 r 
d 
m.
 F  m.  (  r )  2.m.( 
)  m.
 r (6.1)
dt 2
dt
dt
Força centrifuga
Força de Coriolis
A expressão anterior 6.1 é a expressão da Segunda
Lei de Newton para um referencial girante. Se a velocidade
angular () do referencial girante é constante no tempo
o último termo de 6.1 se reduz a zero,


  
 d *r
d *2 r 
m.
 F  m.  (  r )  2.m.( 
) (7.1)
dt 2
dt
18
Algumas conseqüências do
Teorema de Coriolis
19
Aceleração da gravidade efetiva


  
 d *r
d *2 r 
m. 2  F  m.  (  r )  2.m.( 
)
dt
dt


F  m.g
Se assumimos uma partícula
*
d r
de massa m em repouso
0
dt
próxima à superfície do
*2 
d r 
planeta, temos:
 g efetivo
2
dt
  


m.g efetivo  m.g  m.  (  r )  2.m.(  0)

   
g efetivo  g    (  r )
20
21
Efeito da força de Coriolis sobre a circulação
geral do ar atmosférico
22
centro de baixa pressão
Ciclone anti-horário no hemisfério
norte resultante de um centro de
baixa pressão combinado com
a aceleração devida ao termo de
Coriolis.
(Física, um curso universitário, Vol.1- Mecânica; Alonso e Finn;
Editora Edgard Blücher Ltda, 1972).
23
Mesma situação no
hemisfério sul. O sentido
de rotação é o reverso
do hemisfério norte!
(Física, um curso universitário, Vol.1- Mecânica; Alonso e Finn;
Editora Edgard Blücher Ltda, 1972).
24
25
Parte II -Tipos básicos de fluxo
• Fluxo ou escoamento laminar
• Fluxo turbulento
26
Fluxo laminar
27
28
cilindro
Vortices von Karman formados atrás de um cilindro. Fotografado por
Sadatoshi Toneda por precipitação eletrolítica em água (An Album of Fluid
Motion , M.Van Dyke, Parabolic Press, Stanford, California,USA, 1982).
29
30
Fluid Mechanics of the Atmosphere, R. A. Brown, Academic Press, Inc., 1991)
31
Fluid Mechanics of the Atmosphere, R. A. Brown, Academic Press, Inc., 1991)
32
Teresópolis, Fevereiro de 2006. Autor: Prof. Helio S. Amorim
33
Teresópolis, Fevereiro de 2006. Autor: Prof. Helio S. Amorim
34
Teresópolis, Fevereiro de 2006. Autor: Prof. Helio S. Amorim
35
Transição do regime laminar para o turbulento formando-se atrás de uma
esfera.
Fluid Mechanics of the Atmosphere, R. A. Brown, Academic Press, Inc., 1991)
36
37
38
FIM
39