Notas de Aula

U NIVERSIDADE F EDERAL DO PARANÁ — UFPR
C AMPUS AVANÇADO EM J ANDAIA DO S UL
L ICENCIATURA EM C OMPUTAÇÃO
L ICENCIATURA EM C IÊNCIAS E XATAS
Disciplina:
Disciplina:
JLC048 — Pré-Cálculo Professor: Carlos Galvão
JCE023 — Matemática I Professor: Carlos Galvão
Trigonometria — 2016_1 — Notas de Aula
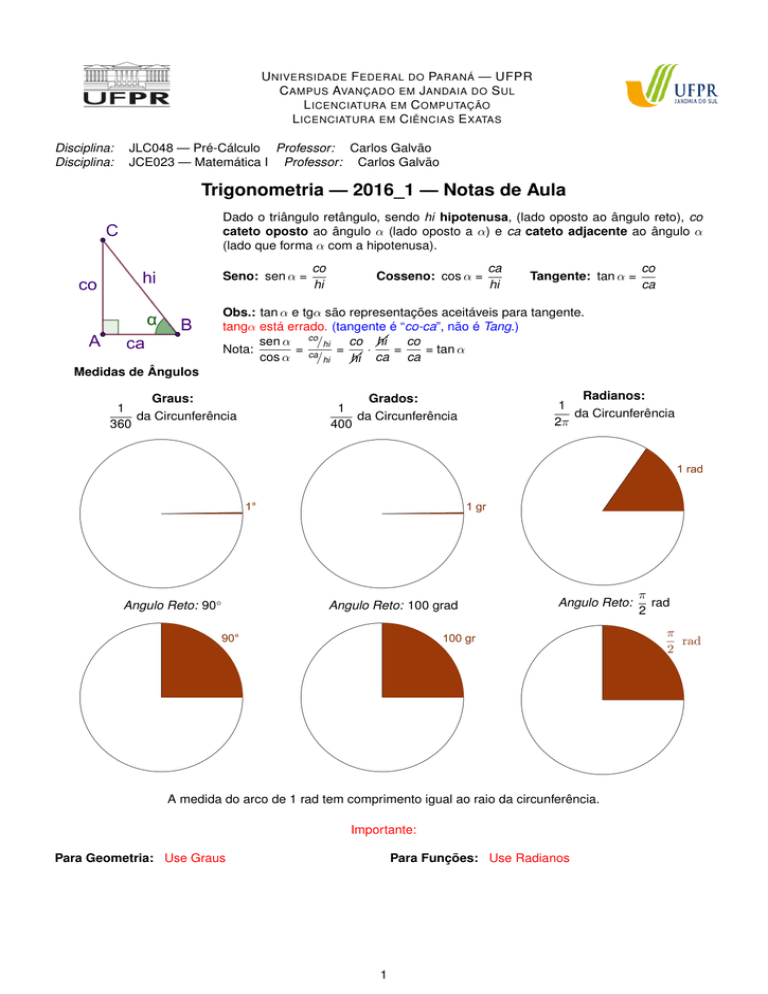
Dado o triângulo retângulo, sendo hi hipotenusa, (lado oposto ao ângulo reto), co
cateto oposto ao ângulo α (lado oposto a α) e ca cateto adjacente ao ângulo α
(lado que forma α com a hipotenusa).
Seno: sen α =
co
hi
Cosseno: cos α =
ca
hi
Tangente: tan α =
co
ca
Obs.: tan α e tgα são representações aceitáveis para tangente.
tangα está errado. (tangente é “co-ca”, não é Tang.)
sen α co/hi co hi
co
Nota:
=
=
=
= tan α
·
cos α ca/hi
hi ca ca
Medidas de Ângulos
Graus:
1
da Circunferência
360
Grados:
1
da Circunferência
400
Radianos:
1
da Circunferência
2π
Angulo Reto: 90◦
Angulo Reto: 100 grad
Angulo Reto:
A medida do arco de 1 rad tem comprimento igual ao raio da circunferência.
Importante:
Para Geometria: Use Graus
Para Funções: Use Radianos
1
π
rad
2
Circunferência Trigonométrica
Circunferência de centro na origem e raio 1.
Todos os ângulos menores do que uma volta podem ser marcados
Medida Vertical: Seno do Ângulo.
Medida Horizontal: Cosseno do Ângulo
Quadrantes
1◦ Quadrante: 0◦ ≤ x ≤ 90◦
3◦ Quadrante: 180◦ ≤ x ≤ 270◦
2◦ Quadrante: 90◦ ≤ x ≤ 180◦
4◦ Quadrante: 270◦ ≤ x ≤ 360◦
Ângulos acima do ângulo reto: Rebate para um ângulo correspondente do 1◦ Quadrante
Para x no 2◦ Quadrante:
sen x = sen (180◦ − x)
cos x = − cos(180◦ − x)
Ex.: sen 156◦ = sen 24◦
cos 156◦ = − cos 24◦
Para x no 3◦ Quadrante:
sen x = −sen (180◦ + x)
cos x = − cos(180◦ + x)
Ex.: sen 216◦ = −sen 56◦
cos 216◦ = − cos 56◦
Para x no 4◦ Quadrante:
sen x = −sen (360◦ − x)
cos x = cos(360◦ − x)
Ex.: sen 302◦ = −sen 58◦
cos 302◦ = cos 58◦
Ângulos Congruentes:
Ângulos com medida abaixo de 0◦ (0 rad ) ou acima de 360◦ (2π rad )
Procedimento: Precisa acrescentar
(para x < 0) ou retirar (para
x > 360◦ ) as voltas extras. Faz-se a
divisão na chave e o ângulo
procurado será o resto desta divisão
Exemplo
489◦
360◦
◦
360
1 volta
◦
129
2
Para x em graus, 0◦ ≤ θ ≤ 360◦ :
x = θ + k · 360◦ , (k ∈ Z)
Para x em radianos,
0 rad ≤ θ ≤ 2π rad :
x = θ + k · 2π rad , (k ∈ Z)
Ângulos Notáveis
◦
Ângulos do 1 Quadrante
◦
rad
sen
cos
tan
π
/6
π
/4
π
/3
1
√
3
√
2
√
2
3
1
◦
30
◦
/2
45
◦
/2
√
60
/2
√
/2
/2
/2
Quartos de Volta
◦
sen
rad
cos
tan
0◦ ou 360◦
0
1
0
/2
90◦
1
0
@
π
180◦
0
−1
0
270◦
−1
0
@
0 ou 2π
3
/3
π
1
√
3
3π
/2
Soma de Arcos
• sen (a ± b) = sen a · cos b ± sen b · cos a
• sen 2a = 2 · sen a · cos a
• cos (a ± b) = cos a · cos b ∓ sen a · sen b
• cos 2a = cos2 a − sen 2 a = 1 − 2sen 2 a = 2 cos2 a − 1
Outras fórmulas, obtidas das anteriores
tan a + tan b
1 − tan a tan b
2 tan a
• tan (2a) =
1 − tan2 a
• sen (x + 2π) = sen x (Período do seno 2π)
• tan (a ± b) =
• cos(x + 2π) = cos x (Período do cosseno 2π)
• tan(x + π) = tan x (Período da tangente π)
π
• sen x +
= cos x para qualquer x.
2
• sen (−x) = −sen x (seno é ímpar)
• cos(−x) = cos x (cosseno é par)
Mais funções trigonométricas
Secante: sec x =
1
cos x
Cossecante: csc x =
1
sen x
Obs.: Ainda é possível escrever cot x =
Cotangente: cot x =
cos x
csc x
=
sen x sec x
Identidades trigonométricas
1 + cot2 α = csc2 α
sen 2 α + cos2 α = 1
tan2 α + 1 = sec2 α
3
1
tan x
rad
◦
0 ou 2π
0◦ ou 360◦
π
/6
π
/4
π
/3
30◦
45◦
60◦
Valores diversos - Não é preciso decorar
sen
cos
tan
sec
csc
0
1
√
1
/2
√
/2
√
2
/2
√
3
3
/2
2
0
√
3
/3
/2
1
√
3
/2
1
1
2 √
/
3
2 √
/
=
2
cot
@
√
2 3
=
2
2
3 √
/
2
/3
√
@
2 √
/
2 √
/
3
2
=
=
√
3
2
√
2 3
/3
=
1 √
/
√
3
=
90◦
1
0
@
@
1
0
π
180◦
0
−1
0
−1
@
@
270◦
−1
0
@
@
−1
0
3π
/2
3
1
/2
π
√
3
/3
Gráficos
Ângulos entre 0 e 2π
Gráficos f (x) com domínio R
As linhas verticais pontilhadas são os valores onde as funções não são definidas. São chamadas assíntotas
4
Funções Trigonométricas Inversas
arco seno sen θ = x ⇔ θ = arcsenx: θ é o arco cujo seno vale x (
−π
π
≤ θ ≤ );
2
2
arco cosseno cos θ = x ⇔ θ = arccos x: θ é o arco cujo cosseno vale x (0 ≤ θ ≤ π);
arco tangente tan θ = x ⇔ θ = arctan x: θ é o arco cuja tangente vale x (
π
−π
≤ θ ≤ ).
2
2
LEIS GERAIS - VALE PARA QUALQUER TRIÂNGULO
Lei dos Cossenos
Lei dos Senos
a2 = b2 + c 2 − 2bc cos Â
sen  sen B̂ sen Ĉ
=
=
a
b
c
b2 = a2 + c 2 − 2ac cos B̂
c 2 = a2 + b2 − 2ab cos Ĉ
5