FIS-26 — Lista-10 — Maio/2013

FIS-26 — Lista-10 — Maio/2013
———————————————————————————
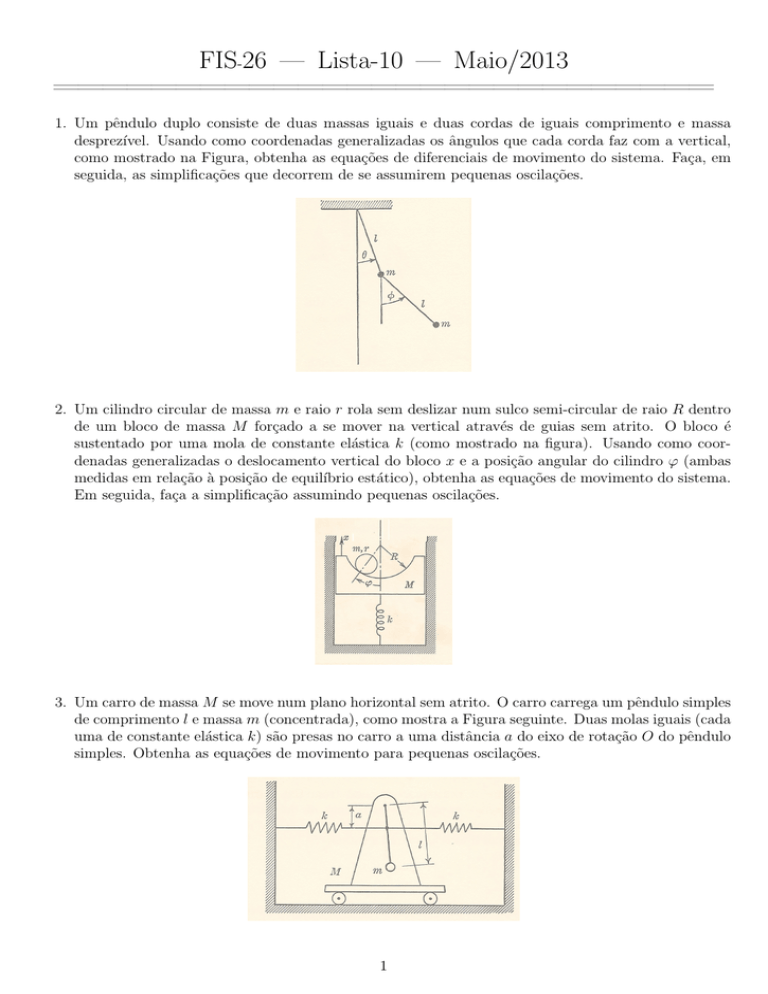
1. Um pêndulo duplo consiste de duas massas iguais e duas cordas de iguais comprimento e massa
desprezı́vel. Usando como coordenadas generalizadas os ângulos que cada corda faz com a vertical,
como mostrado na Figura, obtenha as equações de diferenciais de movimento do sistema. Faça, em
seguida, as simplificações que decorrem de se assumirem pequenas oscilações.
2. Um cilindro circular de massa m e raio r rola sem deslizar num sulco semi-circular de raio R dentro
de um bloco de massa M forçado a se mover na vertical através de guias sem atrito. O bloco é
sustentado por uma mola de constante elástica k (como mostrado na figura). Usando como coordenadas generalizadas o deslocamento vertical do bloco x e a posição angular do cilindro ϕ (ambas
medidas em relação à posição de equilı́brio estático), obtenha as equações de movimento do sistema.
Em seguida, faça a simplificação assumindo pequenas oscilações.
3. Um carro de massa M se move num plano horizontal sem atrito. O carro carrega um pêndulo simples
de comprimento l e massa m (concentrada), como mostra a Figura seguinte. Duas molas iguais (cada
uma de constante elástica k) são presas no carro a uma distância a do eixo de rotação O do pêndulo
simples. Obtenha as equações de movimento para pequenas oscilações.
1
4. Determine o momento no eixo do mecanismo a seguir que produz uma velocidade angular constante
ω em torno do eixo x. A velocidade angular φ̇ = p é mantida constante. O bloco retangular preso
ao eixo A − A tem massa m e os demais componentes têm massa desprezı́vel.
5. Um plano inclinado de massa M pode deslizar livremente numa superfı́cie plana horizontal. Se o
bloco de massa m pode deslizar pela superfı́cie do plano inclinado (como mostra a Figura seguinte),
obtenha as acelerações a1 = ẍ1 e a2 = ẍ2 .
6. Considere uma corda flexı́vel com densidade linear de massa igual a µ e presa em cada extremidade a
suportes rı́gidos de distância l um do outro. A corda está sujeita a uma tensão F , assumida constante
para pequenos deslocamentos da corda.
(a) Mostre que a energia potencial do sistema é:
Z 2
F l ∂y
dx,
V =
2 0 ∂x
onde y é a deflexão da corda (perpendicular a seu comprimento).
(b) Aplique o princı́pio de Hamilton e obtenha a equação de onda:
∂ 2y
µ ∂ 2y
=
.
∂x2
F ∂t2
(c) Qual a velocidade de propagação de ondas nesta corda?
7. Mostre que se a função Lagrangiana L não depende explicitamente de t então a função Hamiltoniana
H é constante.
2
8. Uma partı́cula de massa m é forçada a se mover na superfı́cie de um cilindro de raio a, sendo atraı́da
para a origem por uma força proporcional à distância da partı́cula à origem. Obtenha a Hamiltoniana
e as equações de Hamilton para o movimento.
9. Uma partı́cula de massa m se move em apenas uma dimensão sob a ação da força:
F (x, t) =
k −t/τ
e
,
x2
sendo k e τ constantes. Obtenha as funções Lagrangiana e Hamiltoniana. Obtenha as equações de
Hamilton para o movimento. H é constante? H é a energia total? Derive as equações de movimento.
10. Em 1696, Jean Bernoulli propôs aos matemáticos da Europa o seguinte problema: Uma conta de
colar deve ir de um ponto A até um outro ponto B deslizando ao longo de um fio rı́gido; sabendo
que o ponto A está situado acima do B, mas que os pontos A e B não pertencem a uma mesma
vertical, e supondo irrelevantes os possı́veis atritos, pede-se calcular que forma deve ter o fio-guia a
fim de que a conta sendo abandonada no ponto A chegue ao B no menor tempo possı́vel. Resolva
este problema.
3
Respostas
1. 2θ̈ + φ̈ = (−2g/l)θ,
θ̈ + φ̈ = (−g/l)φ.
2.
3
(R
2
− r)ϕ̈ + ẍ sin ϕ + g sin ϕ = 0,
(M + m)ẍ + m(R − r)ϕ̈ sin ϕ + m(R − r)ϕ̇2 cos ϕ + kx = 0.
3. mlẍ + 2kax + ml2 φ̈ + (mgl + 2ka2 )φ = 0,
(M + m)ẍ + 2kx + mlφ̈ + 2kaφ = 0.
4. M =
1
m(c2
12
5. a1 =
−mg sin θ
m cos2 θ−M −m
− a2 )pω sin(2φ).
e a2 =
mg sin θ cos θ
.
m cos2 θ−M −m
6.
7.
8. H(r, pr , pθ ) =
1
2m
p2r +
p2θ
r2
− kr . Equações do movimento: ṗr =
9.
10. Cicloide ligando os pontos A e B.
4
p2θ
mr3
−
k
, ṗθ
r2
= 0, ṙ =
pr
, θ̇
m
=
pθ
.
mr2