∑ ∑ - Prof Willian

Resistência dos Materiais
Exercícios de Tensão normal
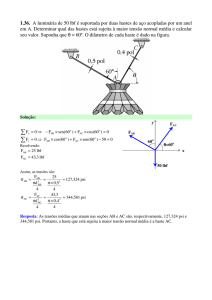
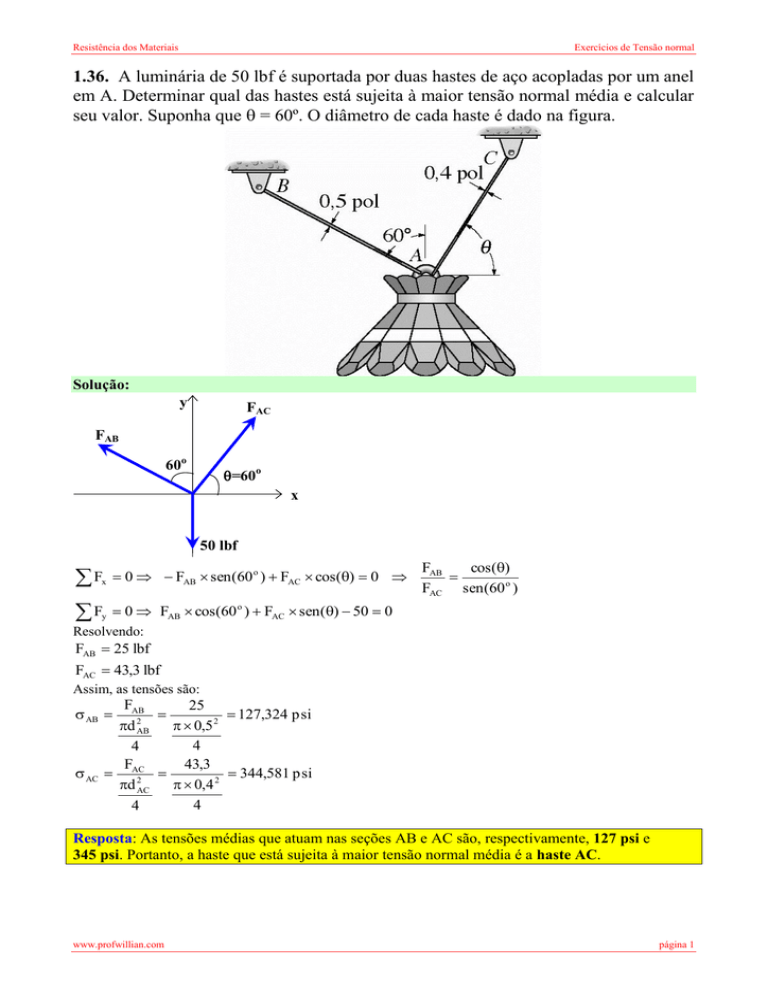
1.36. A luminária de 50 lbf é suportada por duas hastes de aço acopladas por um anel
em A. Determinar qual das hastes está sujeita à maior tensão normal média e calcular
seu valor. Suponha que  = 60º. O diâmetro de cada haste é dado na figura.
Solução:
y
FAC
FAB
60o
=60o
x
50 lbf
F
 0   FAB  sen (60 o )  FAC  cos()  0 
F
 0  FAB  cos(60 o )  FAC  sen ()  50  0
x
y
FAB
cos()

FAC sen (60 o )
Resolvendo:
FAB  25 lbf
FAC  43,3 lbf
Assim, as tensões são:
FAB
25

 127,324 psi
2
d AB
  0,5 2
4
4
F
43,3
 AC2 
 344,581 psi
d AC
  0,4 2
4
4
 AB 
 AC
Resposta: As tensões médias que atuam nas seções AB e AC são, respectivamente, 127 psi e
345 psi. Portanto, a haste que está sujeita à maior tensão normal média é a haste AC.
www.profwillian.com
página 1
Resistência dos Materiais
Exercícios de Tensão normal
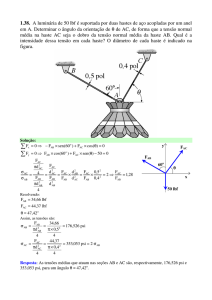
1.37. A luminária de 50 lbf é suportada por duas hastes de aço acopladas por um anel
em A. Determinar qual das hastes está sujeita à maior tensão normal média e calcular
seu valor. Suponha que  = 45º. O diâmetro de cada haste é dado na figura.
Solução:
y
FAC
FAB
60o
=45o
x
50 lbf
F
 0   FAB  sen (60 o )  FAC  cos()  0 
F
 0  FAB  cos(60 o )  FAC  sen ()  50  0
x
y
FAB
cos()

FAC sen (60 o )
Resolvendo:
FAB  36,6 lbf
FAC  44,83 lbf
Assim, as tensões são:
FAB
36,6

 186,415 psi
2
d AB
  0,5 2
4
4
F
44,83
 AC2 
 356,736 psi
d AC
  0,4 2
4
4
 AB 
 AC
Resposta: As tensões médias que atuam nas seções AB e AC são, respectivamente, 186 psi e
357 psi. Portanto, a haste que está sujeita à maior tensão normal média é a haste AC.
www.profwillian.com
página 2
Resistência dos Materiais
Exercícios de Tensão normal
1.38. A luminária de 50 lbf é suportada por duas hastes de aço acopladas por um anel
em A. Determinar o ângulo da orientação de  de AC, de forma que a tensão normal
média na haste AC seja o dobro da tensão normal média da haste AB. Qual é a
intensidade dessa tensão em cada haste? O diâmetro de cada haste é indicado na
figura.
Solução:
 Fx  0   FAB  sen(60 o )  FAC  cos()  0 
F
y
 AC
 AB
FAC sen (60 o )

FAB
cos()
 0  FAB  cos(60 o )  FAC  sen ()  50  0
FAC
FAC
d 2AC
d2
F
F
F
d2
0,5 2
 4  AC  AC  2AB  AC 
 2  AC  1,28
2
FAB
FAB FAB d AC FAB 0,4
FAB
2
2
d AB
d AB
4
y
FAC
FAB
60o

x
50 lbf
Resolvendo (equação 1 com a 3):
  47,42 o
FAB  34,66 lbf
FAC  44,37 lbf
Assim, as tensões são:
FAB
34,66

 176,526 psi
2
d AB
  0,5 2
4
4
F
44,37
 AC  AC2 
 353,053 psi  2  AB
d AC
  0,4 2
4
4
Resposta: As tensões médias que atuam nas seções AB e AC são, respectivamente, 177 psi e
353 psi, para um ângulo  = 47,4o.
 AB 
www.profwillian.com
página 3
Resistência dos Materiais
Exercícios de Tensão normal
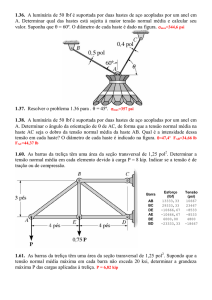
1.60. As barras da treliça têm uma área da seção transversal de 1,25 pol 2. Determinar
a tensão normal média em cada elemento devido à carga P = 8 kip. Indicar se a tensão
é de tração ou de compressão.
Solução:
3
 0,6
5
4
cos    0,8
5
sen  

F
Nó A
y
NAB

A
NAE
 N AB 
F
x
Nó E
F
NBE
y
 0  N AE  N AB cos   0  N AE   N AB  0,8
x
NDE
P
www.profwillian.com
P
 0,8  10,67 kip
0,6
 0  N BE  0,75P  0  N BE  0,75P
 N BE  0,75  8  6 kip
F
E
P
0,6
8
 13,33 kip
0,6
 N AE  
P
NAE
 0   P  N AB sen   0  N AB 
 0  N DE  N AE  0  N DE  N AE
 N DE  
P
 0,8  10,67 kip
0,6
página 4
Resistência dos Materiais
Exercícios de Tensão normal
F
y
Nó B
B
NBC

NAB
 N BD 
F
x
NBE
NBD
 0   N AB sen   N BDsen   N BE  0
 N BE  N AB  0,6
 0,75P  P / 0,6
 N BD 
 23,33 kip
0,6
0,6
 0  N BC  N BD cos   N AB cos   0
 N BC  N AB  0,8  N BD  0,8 
P
 0,75P  P / 0,6
 0,8 
 0,8
0,6
0,6
 N BC  29,33 kip
Resposta: Os valores dos esforços e das tensões de tração (indicadas com +) e de compressão
(indicadas com –) podem ser resumidos na tabela abaixo.
Barra
AB
BC
DE
AE
BE
BD
www.profwillian.com
Esforço (kip)
+13,33
+29,33
-10,67
-10,67
+6,00
-23,33
Tensão (ksi)
+10,67
+23,47
-8,53
-8,53
+4,80
-18,67
página 5
Resistência dos Materiais
Exercícios de Tensão normal
1.61. As barras da treliça têm uma área da seção transversal de 1,25 pol2. Supondo
que a tensão normal média máxima em cada barra não exceda 20 ksi, determinar a
grandeza máxima P das cargas aplicadas à treliça.
Solução:
3
 0,6
5
4
cos    0,8
5
sen  

Nó A
 0   P  N AB sen   0  N AB 
F
 0  N AE  N AB cos   0  N AE   N AB  0,8
y
NAB

A
NAE
x
 N AE  
P
Nó E
NBE
E
 0  N BE  0,75P  0  N BE  0,75P
F
 0  N DE  N AE  0  N DE  N AE
y
NDE
P
www.profwillian.com
P
 0,8  1,333P
0,6
F
x
NAE
P
 1,667P
0,6
F
 N DE  
P
 0,8  1,333P
0,6
página 6
Resistência dos Materiais
Exercícios de Tensão normal
F
y
Nó B
B
NBC

NAB
 N BD 
F
x
NBE
NBD
 0   N AB sen   N BDsen   N BE  0
 N BE  N AB  0,6
 0,75P  P / 0,6
 N BD 
 2,917P
0,6
0,6
 0  N BC  N BD cos   N AB cos   0
 N BC  N AB  0,8  N BD  0,8 
P
 0,75P  P / 0,6
 0,8 
 0,8
0,6
0,6
 N BC  3,667P
Os valores dos esforços e das tensões de tração (indicadas com +) e de compressão (indicadas
com –) podem ser resumidos na tabela abaixo. A tensão normal média máxima ocorre na barra BC.
Barra
AB
BC
DE
AE
BE
BD
Assim:
força

  adm   max
A
Esforço
+1,667P
+3,667P
-1,333P
-1,333P
+0,750P
-2,917P
 20 ksi  2,933P  P 
Tensão
+1,333P
+2,933P
-1,067P
-1,067P
+0,600P
-2,333P
20
2,933
 P  6,818 kip
Resposta: A grandeza máxima P das cargas aplicadas à treliça deve ser de 6,82 kip.
www.profwillian.com
página 7