1 INE 5122 – Instruções para utilização do arquivo Estima.xls O

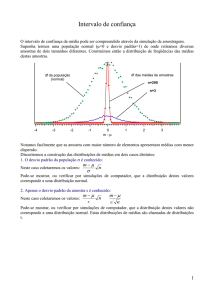
INE 5122 – Instruções para utilização do arquivo Estima.xls
O objetivo do exercício é fixar os conceitos de distribuição amostral da média e intervalo de confiança. Siga os
passos a seguir:
1) Abra o arquivo Estima.xls, procure pela planilha “Dados”. Ela contém os resultados de uma pesquisa de mercado
com 1000 clientes sobre um produto congelado, com as seguintes variáveis: Caso (número da entrevista), Probabilidade
(chance de um cliente ser selecionado na amostragem – igual para todos, 0,001), Sexo, Divulgação (como o cliente
conheceu o produto), Renda (em salários mínimos), Preço (opinião sobre o preço do produto), Praticidade (opinião
sobre praticidade), Sabor (opinião sobre sabor), Npessoas (número de pessoas residindo no domicílio do cliente).
2) Observe a distribuição da variável Renda: média (7,93 salários mínimos), desvio padrão (3,98661 salários mínimos),
e o histograma das rendas (que indica uma distribuição ASSIMÉTRICA). Trata-se então do comportamento da variável
na população.
3) Passe para a planilha Renda2. Você vai pedir para o Excel tirar 100 amostras de tamanho 2 da população.
- no menu Ferramentas selecione “Análise de Dados”;
- em “Análise de Dados” escolha “Geração de Número Aleatório”, e preencha os campos da seguinte forma:
Número de variáveis: 2 significa que a amostra terá
2 elementos;
Número de números aleatórios: 100 significa que
serão retiradas 100 amostras (de 2 elementos, no
caso).
Distribuição: Discreta significa que utilizaremos
uma distribuição de probabilidade definida por nós,
no caso os valores do Intervalo de entrada de
probabilidade e valor (que contém os números dos
casos, de 1 a 1000, e a probabilidade de cada um
ocorrer, que é a mesma para todos, 0,001, na
planilha Dados, simulando uma amostra aleatória
simples).
O intervalo de saída será a partir da célula A3 da
planilha Renda2. O resultado será obtido assim que
for pressionado “OK”
4) O Excel irá selecionar os números dos casos e recuperará os valores de renda correspondentes, nas 100 amostras,
além de calcular média, desvio padrão, e intervalo de 95% de confiança (limites inferior e superior) para a média
populacional a partir dos resultados de cada amostra.
5) O Excel tamb ém calcula a média das 100 médias amostrais (célula J9), e o desvio padrão das médias amostrais
(célula J10). É possível comparar com a média populacional (7,93) e o desvio padrão populacional dividido pela raiz
quadrada do tamanho de amostra:
- Perceba que a média das médias amostrais aproxima-se do valor da média populacional. Isto indica que a
média amostral é um bom estimador da média populacional.
- Perceba que o desvio padrão das médias amostrais aproxima-se do valor do desvio padrão populacional
dividido pela raiz quadrada do tamanho da amostra (2,818967).
6) Agora é preciso observar o formato da distribuição das médias. Veja que o Excel definiu dez classes de valores, que
você utilizará para construir um histograma das médias amostrais:
- no menu Ferramentas selecione “Análise de Dados”;
- em “Análise de Dados” escolha “Histograma”, e preencha os campos da seguinte forma:
O intervalo de entrada contém as médias das 100
amostras (nas células E3 até E102).
O intervalo de bloco contém as classes definidas
pelo Excel a partir dos dados.
O intervalo de saída pode ser qualquer célula
vazia, aqui arbitrariamente escolheu-se a célula
K31.
Temos que marcar “Resultado do Gráfico” para
que o Excel realmente construa o histograma.
O resultado deverá ser semelhante ao da figura
abaixo:
1
40
20
0
19
,00
15
,00
11
,00
Freqüência
7,0
0
3,0
0
Freqüência
Histograma
Bloco
Observe que a distribuição das médias amostrais é
assimétrica, o que é esperado, pois a distribuição da
renda na população é assimétrica e a amostra tem apenas
2 elementos.
Para maiores tamanhos de amostra, o histograma tenderá
cada vez mais a uma normal.
Histograma
M
ai
s
19
,00
17
,00
15
,00
13
,00
11
,00
9,
00
7,
00
5,
00
30
25
20
15
10
5
0
3,
00
Freqüência
Você pode modificar o gráfico para ver melhor o
resultado: remova a legenda freqüência e aumente o
tamanho do gráfico; clique sobre as barras e com o
botão direito do mouse escolha “Formatar série de
dados”, e nesta escolha “Opções ”. Em “Opções” faça
com que a largura do espaçamento entre as barras seja
igual a zero. O gráfico com todas as modificações
sugeridas deverá ser semelhante ao da figura abaixo:
Bloco
7) Você deve ter visto tamb ém um gráfico chamado “Limites de 95% para a média – n = 2”, que apresenta os intervalos
de 95% de confiança para as médias populacionais, com base nos dados das 100 amostras. A faixa vermelha no centro
do gráfico é o valor da média populacional, 7,93 salários mínimos. Observe como virtualmente todos os intervalos
contêm o valor real do parâmetro: veja os valores dos limites nas colunas G e H. Os intervalos são muito grandes
devido ao pequeno tamanho de amostra, o que os torna praticamente inúteis. Os intervalos ficarão mais precisos quanto
maior for o tamanho da amostra.
8) Agora você pode aplicar raciocínio semelhante na planilha Renda8, para obter amostras de tamanho 8 (número de
variáveis = 8), e na planilha Renda30, para obter amostras de tamanho 30 (número de variáveis = 30).
2