Aula 10 Teoria das pequenas amostras - UFMT

UNIVERSIDADE FEDERAL DE MATO GROSSO
CAMPUS UNIVERSITÁRIO DO ARAGUAIA
INSTITUTO DE CIÊNCIAS EXATAS E DA TERRA
Curso: Engenharia Civil
Disciplina: Estatística (64H)
Aula 10: Teoria das pequenas amostras
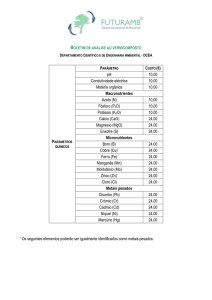
Considera-se que amostras de tamanho N>30, chamadas de grandes amostras, a melhor
aproximação, para as distribuições amostrais é a normal. Essa aproximação melhora com o
crescimento de N.
Quando o tamanho das amostras é N<30 elas são consideradas pequenas amostras e o tratamento
estatístico é diferente.
Para pequenas amostras, as distribuições amostrais consideradas são STUDENT e QUIQUADRADO.
Distribuição de “STUDENT”:
Defini-se a estatística
−
t=
X −µ
∧
s
N
Onde
−
X
(média amostral)
∧
s
(desvio padrão da amostra)
µ
(média da população)
Essa distribuição é dada por:
Y=
Y0
 t2 
1 + 
 ν 
(ν +1) 2
Sendo:
ν = N −1
(Número de Graus de Liberdade)
Y0=Constante dependente de N.
Y
0,4
0,3
Normal
v=4
v=1
0,2
0,1
-3
-2
-1
0
1
2
3
t
Intervalos de confiança:
A média da população µ, pode ser estimada dentro dos limites de confiança especificados.
Por exemplo:
Se -t0,975 e t0,975 são os valores de t, para os quais 2,5% da área ficam localizados em cada
extremidade da distribuição t, então o intervalo de confiançaque é de 95%, para t, é:
−
− t 0.975
X −µ
<
N − 1 < t 0.975
s
Do qual se verifica que µ é estimado para que caia dentro do intervalo:
−
−
s
s
< µ < X + t 0.975
N −1
N −1
X − t 0.975
Com a confiança de 95%. Note-se que t0,975, representa o valor do percentil 97,5, enquanto
t0,025=-t0,975 representa o percentil 2,5.
Distribuição de Qui-Quadrado:
Defini-se a estatística
χ2 =
Ns 2
σ2
Essa distribuição é dada por:
1
Y = Y0 ( χ 2 ) 2
(ν −2 )
−1
e2
χ2
−1
= Y0 χ ν −2 e 2
χ2
Y
0,4
v=2
0,3
0,2
0,1
0
v=4
v=6
v=10
5
Sendo:
ν = N −1
(Número de Graus de Liberdade)
Y0=Constante dependente de ν
10
15
20
t
Intervalos de Confiança:
A partir dos limites de confiança especificados, podemos determinar o desvio padrão
populacional σ, expresso em função dos desvio padrão amostral, s.
Por exemplo, se
χ0,0252 e χ0,9752 são os valores de χ2, para os quais 2,5% da área são localizadas em cada
“extremidade” da distribuição, o intervalo de confiança de 95% é, então:
χ 02.025 <
Ns 2
σ2
< χ 02.975
Do qual se verifica que σ é estimado para que caia dentro do intervalo:
s N
χ 0.975
<s<
s N
σ N
,< σ <
χ 0.025
χ 0.025
Com grau de confiança de 95%. De maneira semelhante, podem ser determinadas outros
intervalos de confiança. Os valores χ0,025 e χ0,975 são os valores dos percentis 2,5 e 97,5.
Graus de liberdade:
Definida pela letra ν, é o número de N observações da amostra (tamanho) menos o número k de
parâmetros populacionais. Assim ν=N-k.