6- Probabilidade e amostras: A distribuição das médias amostrais

6- Probabilidade e amostras:
A distribuição das médias amostrais
• Anteriormente estudamos como atribuir probabilidades a uma
observação de alguma variável de interesse (ex: Probabilidade de um
escore de ansiedade superior a 80, de uma nota inferior a 30,...).
• Vamos considerar agora a situação em que dispomos de n > 1
observações da variável de interesse (ou seja, de uma amostra de n
indivíduos).
2
• Assim como
podemos
associar
probabilidades
a
observações
individuais de uma variável aleatória, podemos também associar
probabilidades a amostras de n observações ou, mais especificamente,
aos valores de alguma estatística de interesse, calculada para as
amostras (como a média amostral).
• Chamamos distribuição amostral de uma estatística a distribuição
dessa estatística em repetidas amostras de uma específica população.
3
• Chamamos erro padrão de uma estatística o desvio padrão da
distribuição dessa estatística em repetidas amostras de uma específica
população.
4
Exemplo 6.1 – Três vendedores são encarregados de fazer, cada um deles,
uma venda. Suponha que para cada venda realizada o vendedor receba 100
reais, e que para cada venda não realizada o vendedor perca 20 reais, em
decorrência de gastos com deslocamento. A probabilidade de cada um
deles realizar sua venda é 0,5.
5
Seja X a variável aleatória que assume valor 100 com probabilidade ½
e -20 com probabilidade ½, referente ao retorno financeiro de cada um dos
vendedores. Sejam X 1 , X 2 , X 3 os retornos dos três vendedores e
X1 + X 2 + X 3
1 n
2
2
(
)
X=
, s =
X
−
X
∑
i
n − 1 i =1
3
a média da amostra de três retornos e a variância. Vamos obter a
distribuição amostral dessas duas estatísticas (média e variância amostrais).
6
Amostra:
( x1 , x2 , x3 )
(− 20,−20,−20)
(− 20,−20,100)
(− 20,100,−20)
(100,−20,−20)
(− 20,100,100)
(100,−20,100)
(100,100,−20)
(100,100,100)
Probabilidade
x
s2
1/8
-20
0
1/8
20
4800
1/8
20
4800
1/8
20
4800
1/8
60
4800
1/8
60
4800
1/8
60
4800
1/8
100
0
7
Assim, com base nas probabilidades associadas a cada amostra,
podemos associar probabilidades aos diferentes valores de x e de s 2 ,
produzindo as seguintes distribuições amostrais:
• Distribuição amostral de x :
x
-20
20
60
100
Probabilidade
1/8
3/8
3/8
1/8
s2
0
4800
Probabilidade
2/8
6/8
• Distribuição amostral de s 2 :
8
• Diferentemente do exemplo apresentado, em geral não é possível
enumerar todas as amostras possíveis, sendo impraticável obter a
distribuição amostral de estimadores da forma realizada.
• No entanto, dispomos de resultados que nos permitem estabelecer a
distribuição amostral de estimadores sem a necessidade de enumerar
todas as amostras possíveis.
• Vamos nos ater, num primeiro momento, ao estudo da distribuição das
médias amostrais, fundamental para investigar (estimar) a média de
toda a população.
9
Distribuição das médias amostrais
• Considere uma população com média µ e desvio padrão σ (lembre-se
que µ e σ são parâmetros, quantidades que descrevem a população,
sendo, geralmente, desconhecidos.
• Seja x a média de uma amostra aleatória de tamanho n ( x1 , x2 ,..., xn ) da
população sob estudo.
10
• Um primeiro resultado geral diz respeito ao centro da distribuição
amostral de x (ou seja, da distribuição dos valores de x calculados com
base em repetidas amostras extraídas da população).
A média da distribuição das médias amostrais, denotada por µ x , é igual a
média da população, ou seja, µ x = µ .
Nota – Este resultado nos garante que seja qual for o tamanho da amostra
( n ) os valores de x calculados para repetidas amostras estarão centrados na
média da população.
11
• Um segundo resultado geral diz respeito à dispersão da distribuição
amostral de x .
O desvio padrão da distribuição das médias amostrais (ou seja, o erro
padrão de x ), denotada por σ x , é igual ao desvio padrão da população
dividido por n , ou seja, σ x = σ
n.
Nota – Observe que a dispersão da distribuição de x diminui conforme se
aumenta o tamanho da amostra ( n ).
12
• Com base nos dois resultados apresentados até o momento temos que, a
medida que aumentamos o tamanho da amostra, os valores das médias
de repetidas amostras de tamanho n estarão distribuídos cada vez mais
próximos, em torno da média da população ( µ ).
• Um último resultado refere-se à forma da distribuição amostral de x .
Se a distribuição da variável de interesse população sob estudo for
normal, então a distribuição das médias amostrais de tamanho n
também é normal (centrada em µ e com desvio padrão σ x = σ
13
n ).
4
3
Densidade
n=1
n=5
n=20
2
n=100
1
0
-3
-2
-1
0
1
2
3
x
Figura 1 – Distribuição amostral das médias de amostras de tamanho n
extraídas de uma população com distribuição normal padrão.
14
Exemplo 6.2 – A distribuição dos escores de habilidade verbal ( x ) em certa
população apresenta distribuição Normal, com média µ = 60 e desvio
padrão σ = 10 . Selecionada aleatoriamente uma amostra de n = 25
indivíduos dessa população:
a) Qual a distribuição amostral de x , o escore médio dos 25 indivíduos
selecionados para a amostra?
b) Qual a probabilidade do escore médio na amostra selecionada ser
inferior a 57? E superior a 62?
15
c) Usando a regra empírica, em qual intervalo de valores teremos
aproximadamente 67% das médias de amostras de 25 indivíduos? O
mesmo para 95 e 99,7%;
d) Como ficaria o item “c” para amostras de tamanho n = 9 ? E para
amostras de tamanho n = 100 ?
• A normalidade da distribuição das médias amostrais vale caso a
distribuição da variável sob estudo tenha distribuição normal. No
entanto,
para
amostras
suficientemente
grandes,
ela
vale
(aproximadamente), independentemente da distribuição da variável sob
16
estudo (que pode, inclusive, ser discreta). Isso é garantido pelo
Teorema Central do Limite.
• Usamos este resultado anteriormente quando discutimos a aproximação
da distribuição binomial pela distribuição Normal.
Nota – Como regra geral, temos que a distribuição das médias de amostras
de tamanho n é bem aproximada pela distribuição normal quando n > 30 .
17
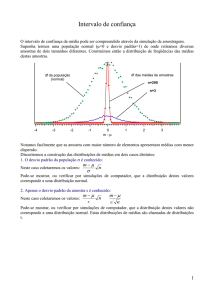
Exemplo 6.3 – Para ilustrar o Teorema Central do Limite, vamos
considerar
uma
variável
aleatória
discreta
com
distribuição
de
probabilidades conforme a Figura 2 apresentada na sequência.
• Usando simulação, foram geradas 10.000 amostras de tamanho n desta
variável, obedecendo às probabilidades apresentadas na Figura 2, para
diferentes valores de n .
18
0.5
0.4
P(X=x)
0.3
0.2
0.1
0.0
0
1
2
3
x
Figura 2 – Distribuição de probabilidades da variável X .
19
n=5
n=10
0.8
Densidade
Densidade
1.0
0.6
0.4
0.2
0.0
0
1
2
3
1.2
1.0
0.8
0.6
0.4
0.2
0.0
4
1.0
1.5
2.0
x
x
n=30
n=100
2.5
3.0
Densidade
Densidade
2.0
1.5
1.0
0.5
0.0
3
2
1
0
1.6
1.8
2.0
2.2
2.4
1.8
x
1.9
2.0
2.1
x
Figura 3 – Ilustração do teorema central do limite.
20
2.2