Intervalo de confiança

Intervalo de confiança
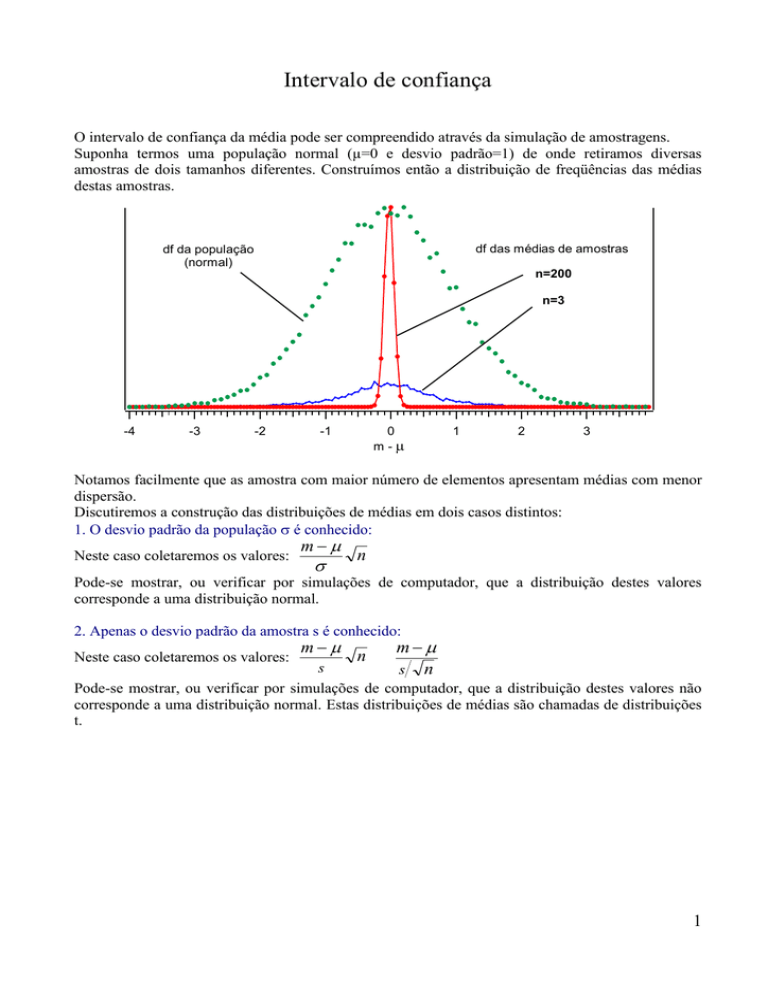
O intervalo de confiança da média pode ser compreendido através da simulação de amostragens.
Suponha termos uma população normal (µ=0 e desvio padrão=1) de onde retiramos diversas
amostras de dois tamanhos diferentes. Construímos então a distribuição de freqüências das médias
destas amostras.
df das médias de amostras
df da população
(normal)
n=200
n=3
-4
-3
-2
-1
0
m -
1
2
3
Notamos facilmente que as amostra com maior número de elementos apresentam médias com menor
dispersão.
Discutiremos a construção das distribuições de médias em dois casos distintos:
1. O desvio padrão da população  é conhecido:
Neste caso coletaremos os valores:
m

n
Pode-se mostrar, ou verificar por simulações de computador, que a distribuição destes valores
corresponde a uma distribuição normal.
2. Apenas o desvio padrão da amostra s é conhecido:
Neste caso coletaremos os valores:
m
n
m
s n
s
Pode-se mostrar, ou verificar por simulações de computador, que a distribuição destes valores não
corresponde a uma distribuição normal. Estas distribuições de médias são chamadas de distribuições
t.
1
m
distrib. das médias:
0.6
n
s
distribuição t
curva normal
0.5
0.4
0.3
0.2
0.1
0.0
-2
-1
0
1
2
n 1
!
1
2
A distribuição t é da forma
2
n2
(1  B)(t  t0 )2  ( B 1) / 2
! 2  (1  t ) (n1)/ 2
A(1 
)
2
B
n
ou
onde B=n-1. Observe que esta distribuição depende explicitamente do tamanho da amostra.
Calculando a área sobre estas distribuições, seja ela normal ou não, podemos calcular a probabilidade
de encontrarmos um valor de média em um determinado intervalo da variável. A área indicada na
curva representa a probabilidade de termos o valor da média entre -2 e +2.
0.30
0.20
0.10
0.00
-4
-2
0
2
4
Analogamente, podemos fixar um valor de probabilidade e calcular um intervalo, chamado de
intervalo de confiança.
P = 95%
-4
-2
0
2
4
Intervalo de confiança de 95%
Portanto, se
2
1. O desvio padrão da população  é conhecido:

 
m
Z 
n
  m  Z 
ou


n

Apenas com o nível de confiabilidade podemos encontrar o valor de Z.

Z
5%
1.644853
10%
1.281552
1%
2.326347
2. Apenas o desvio padrão da amostra s é conhecido:

s 
m
tn, 
n
  m  t n,
ou

s
n

De forma geral, podemos calcular o intervalo de confiança pela seguinte relação, usando valores t
tabelados de acordo com o nível de confiabilidade e o tamanho da amostra
s
s
   m  tn,
n
n
Observe que µ e  são os parâmetros da população e m e s são os parâmetros da
m  tn,
amostra.
O software de estatística calcula este intervalo automaticamente, dispensando o uso
de tabelas.
A interpretação do intervalo de confiança, obtido através de uma amostragem
apenas, pode ser expresso como:
"Supondo que a população seja normal, se repetirmos o experimento
inúmeras vezes, em 95% dos casos teremos a verdadeira média da
população dentro do intervalo de confiança."
Entretanto, como você não conhece a média real da população, você nunca saberá
quando a azarada coincidência de 5% ocorre ou não. Situação análoga a jogar um
dado de 20 faces e acreditar que não caiu o lado 13.
Intervalo de confiança indeterminado
 m
s
n
A conexão entre o intervalo de confiança determinado e o indeterminado: t=1
Podemos portanto verificar para diferentes tamanhos de amostras, qual a
confiabilidade deste intervalo.
3
n=1
n=2
n=5
57,2%
60,0%
63,9%
n=16
n=100
n=infinito
66,8%
68,0%
68.3%
indica que para uma amostra grande (aprox. 100 valores) o intervalo contém 68.3 %
de probabilidade de conter a média da população. Para amostras menores, esta
confiabilidade cai até aprox 60%.
Use portanto o intervalo de 95% ou o indeterminado de acordo com a exatidão
necessária.
4