h - forma moda original

H - FORMA MODA ORIGINAL
Forma de um histograma normal com a última classe com freqüência maior que a
média. Ocorre quando há erro na distribuição das frequências, ou na coleta de dados.
HISTOGRAMAS COM LIMITES DE ESPECIFICAÇÃO
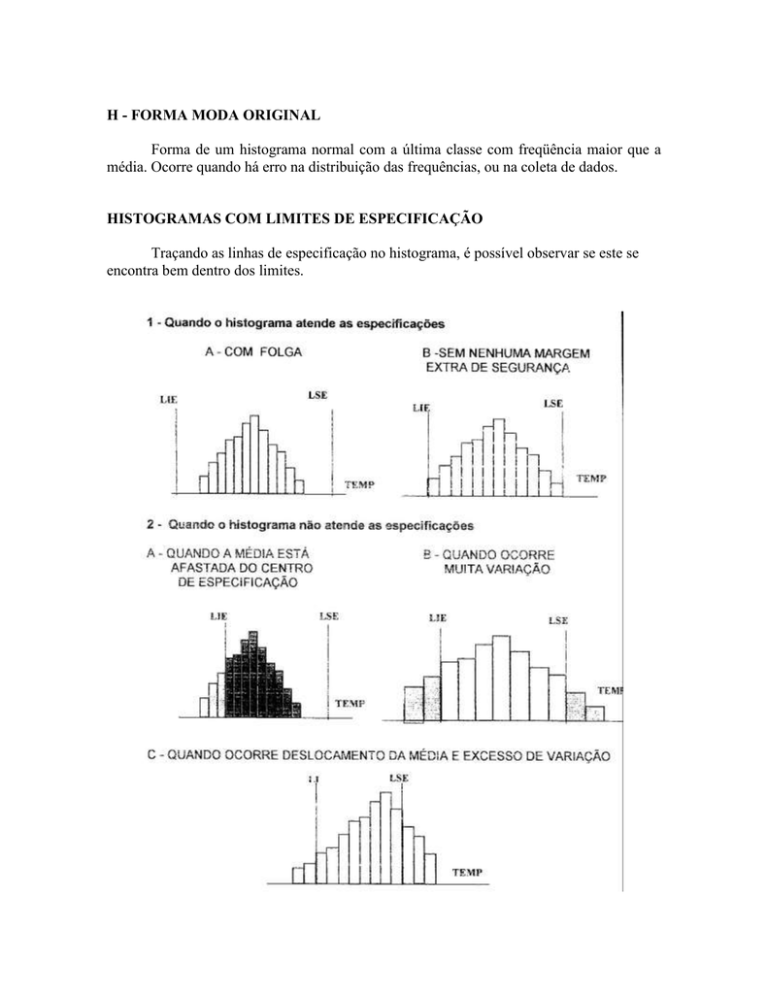
Traçando as linhas de especificação no histograma, é possível observar se este se
encontra bem dentro dos limites.
ESTRATIFICAÇÃO DE HISTOGRAMAS
Quando os valores observados são divididos em duas ou mais sub-populações,
conforme as condições existentes na coleta de dados, tais sub-populações são chamadas de
estratos.
Os valores observados sempre trazem alguma variação. Por sto quando os dados são
estratificados, conforme os fatores suspeitos que provocam as variações, as causas de
variações tornam-se mais facilmente detectáveis. Esse método pode ser usado eficazmente
para aumentar a qualidade do produto, pela redução da variação e ajuste da média do
processo.
A estratificação é geralmente feita conforme os materiais, as máquinas, as
condições de operação e os trabalhadores.
Exercício:
Numa fábrica que produz molas, foram encontradas rachaduras em algumas delas.
Tornando necessário, o mais rápido possível a identificação da causa de problema, e evitar
que o problema volte a ocorrer. As informações obtidas foram:
a)
As molas A1 e A2 foram tratadas no mesmo forno. Os dois tipos diferem somente no
formato. O material que foram feitos é o mesmo, entretanto, o tipo de cesto usado no
tratamento térmico é diferente.
b) O forno é operado em dois turnos diários, B1 e B2 Dois tratamentos térmicos são
realizados por turno.
c) Suspeitou-se que a variação da temperatura do forno, do centro para as paredes,
poderia ser significativa. Portanto, após cada tratamento térmico, uma amostra (P1) foi
retirada do centro do forno e outra (P2) de perto da parede, e suas durezas foram
medidas.
d) Os padrões de dureza são: Máxima 46Ohb, mínima 35OHb.
Utilizando a Tabela 1 a e 1.b construa:
a)
b)
c)
d)
e)
f)
Histograma Global.
Histograma para amostra trincada.
Histogramas para diferentes tipos de mola (A1 e A2).
Histogramas para os diferentes turnos (B1 e B2).
Histogramas para diferentes posições de tratamento térmico (P1 eP2).
Histogramas para diferentes combinações de A e B. (A1 e B1; A1 e B2; Ac e B1; A2 e
B2).
g) Histogramas para diferentes combinações de A, B e P (A1B1P1; A1B1P2; A1B2P1;
A1B2P2; A2B1P1; A2B1P2; A2B2P1; A2B2P2).
Faça uma análise de cada resultado e discuta com seu grupo.
HISTOGRAMA E DISTRIBUIÇÃO NORMAL
Um histograma é construído a partir de um certo número de dados, resultando na
figura já estudada. Porém se continuarmos a aumentar o número de dados e diminuirmos
pouco a pouco o tamanho do intervalo das classes, uma curva suave de distribuição de
freqüência é obtida.
Existem vários tipos de distribuição, mas a mais freqüente é a Distribuição Normal.
Quando a variação de uma característica da qualidade é gerada pela soma de um grande
número de erros infinitesimais independentes devido a diferentes fatores, a distribuição da
característica da qualidade se torna, em muitos casos, aproximadamente uma distribuição
normal. A distribuição normal pode ser simplesmente descrita como tendo a forma de um
sino ou montanha, e uma descrição mais detalhada:
A - a densidade de probabilidade é mais alta no meio e diminui gradualmente em
direção as caudas.
B - ela é simétrica.
A equação da distribuição normal possui dois fatores  e  e é unicamente
terminada por esses dois parâmetros e denotada simplesmente por N(O, 1). Estes dois
parâmetros possuem o seguinte significado:
. O centro da distribuição normal ( a média)
. A dispersão da distribuição normal (o desvio padrão)
Para se obter uma probabilidade em uma distribuição normal, nós realizamos
padronização e usamos a distribuição normal. Padronização é a transformação de na
variável x para:
Z
X 

Teremos então o valor padronizado z, que se distribui como a distribuição normal
padronizada N(0,1)2. A tabela normal fornece probabilidade na distribuição normal
padronizada.
Teoricamente, uma variável normal (z) pode assumir qualquer valor entre (  e
  ), porém, podemos verificar que quando o valor de z coincide com o valor do desvio
padrão, e o marcamos em ambos os lados da média, teremos um bom referencial do valor
das probabilidades, conforme representado na figura abaixo:
11. DIAGRAMA DE PARETO
FINALIDADE:
Gráfico de barras verticais que dispõe a informação de forma a tornar evidente e
visual a priorização de temas. A informação assim disposta, também permite o
estabelecimento de metas numéricas possíveis de alcançadas.
EXEMPLO:
ANÁLISE DE PARETO
DEFINIÇÃO:
Abordagem estatística que permite através de uma representação gráfica especifica,
a identificação dos aspectos relevantes relacionados à qualidade.
PRINCIPIO DE PARETO:
“POUCOS, MAS VITAIS E MUITOS TRIVIAIS”
Exemplo: 20% da população fica com 80% da arrecadação (pouco vitais) e os outros 80%
da população (muitos triviais) fica com apenas 20% da arrecadação: