Trigonometria e funções trigonométricas

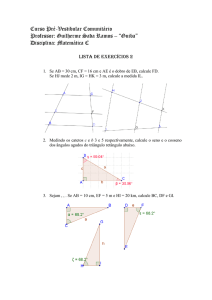
matA11 – trigonometria e funções trigonométricas
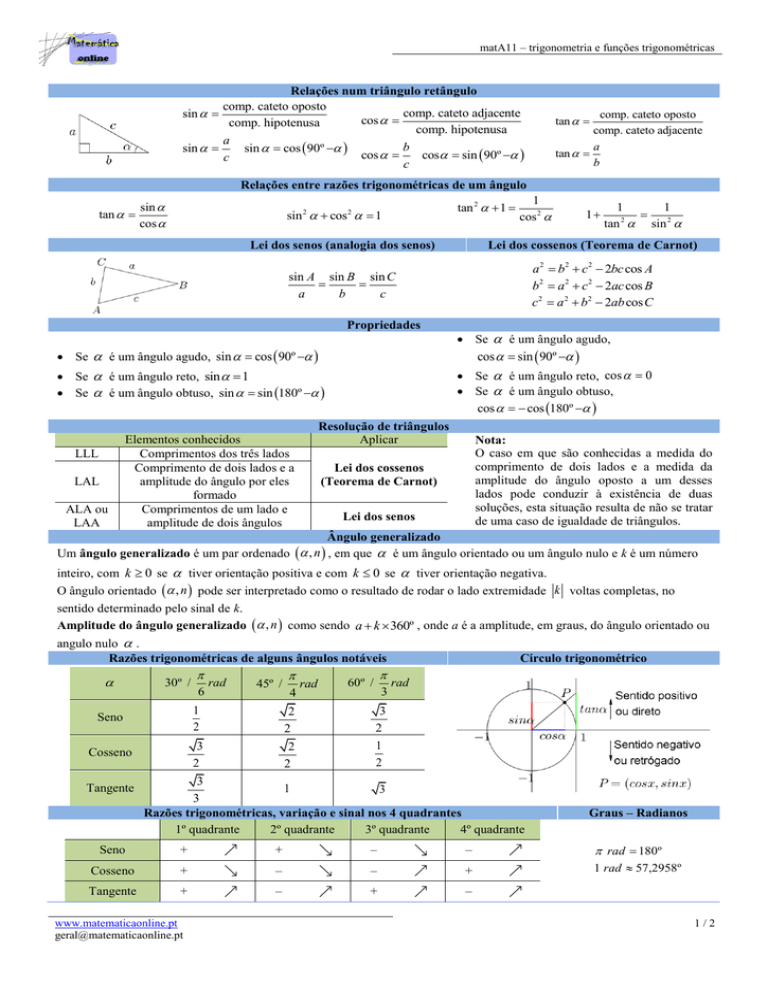
Relações num triângulo retângulo
comp. cateto oposto
comp. cateto adjacente
sin  
cos  
comp. hipotenusa
comp. hipotenusa
a
b
sin  
sin   cos  90º  
cos  
cos  sin  90º  
c
c
comp. cateto oposto
comp. cateto adjacente
a
tan  
b
tan  
Relações entre razões trigonométricas de um ângulo
tan  
sin 
cos 
sin 2   cos 2   1
1
1

2
tan  sin 2 
sin A sin B sin C


a
b
c
a 2  b2  c 2  2bc cos A
b2  a 2  c 2  2ac cos B
c 2  a 2  b2  2ab cos C
Elementos conhecidos
Comprimentos dos três lados
Comprimento de dois lados e a
amplitude do ângulo por eles
formado
Comprimentos de um lado e
amplitude de dois ângulos
 Se  é um ângulo agudo,
cos   sin  90º  
 Se  é um ângulo reto, cos   0
 Se  é um ângulo obtuso,
cos    cos 180º  
 Se  é um ângulo reto, sin   1
 Se  é um ângulo obtuso, sin   sin 180º  
ALA ou
LAA
1
Lei dos cossenos (Teorema de Carnot)
 Se  é um ângulo agudo, sin   cos  90º  
LAL
1
cos 2 
Lei dos senos (analogia dos senos)
Propriedades
LLL
tan 2   1 
Resolução de triângulos
Aplicar
Nota:
O caso em que são conhecidas a medida do
comprimento de dois lados e a medida da
amplitude do ângulo oposto a um desses
lados pode conduzir à existência de duas
soluções, esta situação resulta de não se tratar
de uma caso de igualdade de triângulos.
Lei dos cossenos
(Teorema de Carnot)
Lei dos senos
Ângulo generalizado
Um ângulo generalizado é um par ordenado  , n  , em que  é um ângulo orientado ou um ângulo nulo e k é um número
inteiro, com k  0 se  tiver orientação positiva e com k  0 se  tiver orientação negativa.
O ângulo orientado  , n  pode ser interpretado como o resultado de rodar o lado extremidade k voltas completas, no
sentido determinado pelo sinal de k.
Amplitude do ângulo generalizado  , n  como sendo a  k  360º , onde a é a amplitude, em graus, do ângulo orientado ou
angulo nulo  .
Razões trigonométricas de alguns ângulos notáveis



30º / rad
60º / rad

45º / rad
6
3
4
Seno
1
2
Cosseno
3
2
Tangente
2
2
2
2
Círculo trigonométrico
3
2
1
2
3
1
3
3
Razões trigonométricas, variação e sinal nos 4 quadrantes
1º quadrante
2º quadrante
3º quadrante
4º quadrante
Graus – Radianos
Seno
+
+
–
–
 rad  180º
Cosseno
+
–
–
+
1 rad  57,2958º
Tangente
+
–
+
–
www.matematicaonline.pt
[email protected]
1/2
matA11 – trigonometria e funções trigonométricas
Relações entre razões trigonométricas
sin      sin 
sin       sin 
sin      sin 


sin      cos 
2

cos     cos 


sin      cos 
2

cos       cos 
 3

sin 
     cos 
 2

cos       cos 
 3

sin       cos 
 2



cos      sin 
2

tan      tan 


cos       sin 
2

tan       tan 
 3

cos 
     sin 
 2

tan      tan 
 3

cos 
    sin 
 2

1
1
1


 3

 3

tan      
tan 
  
tan 
   
tan 
tan 
2

 2
 tan 
 2

Função periódica
Uma função f, de domínio Df, diz-se periódica de período P se e só se x  D f , x  P  D f e f  x  P   f  x 
Ao menor período positivo de P de uma função periódica chama-se período positivo mínimo ou período fundamental.
Equações trigonométricas
tan x  tan 
sin x  sin 
cos  x   cos 

x    k , k 
 x    2k  x      2k , k 
 x    2k  x    2k , k 
Função seno
Função inversa da função seno (arco-seno)
Arco-seno
é a função inversa da restrição da função seno ao
f  x   sin x
  
 Domínio:
intervalo   ,  , representa-se por arcsin, nas calculadores
 2 2
 Contradomínio:  1,1
aparece representada por sin 1 .

 Maximizantes:  2k , k 
 Domínio:  1,1
2
1


tan     
2
 tan 
 Minimizantes: 

2
 2k , k 
 Zeros: k , k 
 Período: 2 (Período, fundamental)
 Simetrias: Ímpar
Função cosseno
f  x   cos x
 Domínio:
 Contradomínio:  1,1
 Maximizantes: 2k , k 
 Minimizantes:   2k , k 

 Zeros:  k , k 
2
 Período: 2 (Período, fundamental)
 Simetrias: Par
Função tangente
f  x   tan x



\  x  : x   k , k  
2


Contradomínio:
Zeros: k , k 
Período:  (Período, fundamental)
Simetrias: Ímpar
 Domínio:




  
 Contradomínio:   , 
 2 2
 Zeros: 0
Função inversa da função cosseno (arco-cosseno)
Arco-cosseno é a função inversa da restrição da função
cosseno ao intervalo 0,  , representa-se por arccos, nas
calculadores aparece representada por cos1 .
 Domínio:  1,1
 Contradomínio: 0, 
 Zeros: 1
Função inversa da função tangente (arco-tangente)
Arco-tangente é a função inversa da restrição da função
  
,  , representa-se por arctan,
 2 2
1
nas calculadores aparece representada por tan .
tangente ao intervalo  
 Domínio:
  
, 
 2 2
 Contradomínio:  
 Zeros: 0
 Simetria: Ímpar
www.matematicaonline.pt
[email protected]
2/2